Matematik: Grundlæggende definition og guide til tal, former og analyse
Grundlæggende guide til matematik: forstå tal, former, algebra, geometri og analyse med klare forklaringer og praktiske eksempler for elever og fagfolk.
Matematik er studiet af tal, former og mønstre. Ordet kommer af det græske ord "μάθημα" (máthema), der betyder "videnskab, viden eller læring", og forkortes undertiden til maths (i England, Australien, Irland og New Zealand) eller maths (i USA og Canada). De korte ord bruges ofte af elever og deres skoler om aritmetik, geometri eller simpel algebra.
Matematik omfatter studiet af:
- Tal: hvordan ting kan tælles.
- Struktur: hvordan tingene er organiseret. Dette underområde kaldes normalt algebra.
- Sted: hvor tingene befinder sig og deres placering. Dette underområde kaldes normalt geometri.
- Forandring: hvordan ting bliver anderledes. Dette underområde kaldes normalt analyse.
Matematik er nyttig til at løse problemer, der opstår i den virkelige verden, så der er mange andre end matematikere, der studerer og bruger matematik. I dag er der brug for matematik i mange job. Folk, der arbejder i erhvervslivet, inden for videnskab, teknik og byggeri, har brug for et vist kendskab til matematik.
Taltyper og grundbegreber
Et godt sted at begynde er tal og deres egenskaber. De mest almindelige taltyper omfatter:
- Naturlige tal: 1, 2, 3 … bruges til tælling.
- Hele tal: inkluderer 0 og negative tal (…, −2, −1, 0, 1, 2 …).
- Rationale tal: tal, der kan skrives som brøk a/b, fx 1/2 eller 3.
- Irrationale tal: tal, der ikke kan skrives som en brøk, fx π og √2.
- Reelle tal: alle rationale og irrationale tal—bruges til målinger og kontinuerlige størrelser.
- Komplekse tal: tal på formen a + bi, hvor i² = −1; vigtige i mange områder af fysik og teknik.
Grundlæggende operationer er addition, subtraktion, multiplikation og division. Andre vigtige begreber er primtal, faktorisering, procentregning, brøker og decimaler.
Algebra og struktur
Algebra handler om at arbejde med symboler (variabler) for at beskrive mønstre og relationer. Centrale emner inkluderer:
- Ligninger og uligheder: løsning af for eksempel lineære og kvadratiske ligninger.
- Funktionsbegrebet: hvordan én størrelse afhænger af en anden (fx y = f(x)).
- Polynomer og faktorisering: manipulation af udtryk.
- Lineær algebra: matricer, vektorer og systemer af ligninger—vigtige i computergrafik, dataanalyse og ingeniørarbejde.
- Abstrakt algebra: grupper, ringe og felter—studier af strukturer, der optræder i talteori og kryptografi.
Geometri: former og rum
Geometri beskriver form, størrelse og placering af figurer. Emner spænder fra plan geometri (trekanter, cirkler, polygoner) til rumgeometri (kugler, prismer, volumenberegning). Koordinatgeometri forbinder geometri med algebra ved hjælp af et koordinatsystem, mens transformationer (spejling, rotation, skalering) beskriver bevægelser af figurer.
Analyse (calculus) og forandring
Analyse handler om forandring og bevægelse. De to hoveddele er:
- Differentialregning: beskriver hældning og øjeblikkelig ændring via afledte funktioner.
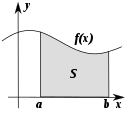
- Integralregning: beregner arealer og akkumuleret mængde via integraler.
Analyse indbefatter også begreber som grænseværdier, kontinuitet og differentialligninger, som bruges til at modellere fysiske systemer, økonomiske processer og meget mere.
Anvendelser og værktøjer
Matematik anvendes bredt:
- Inden for naturvidenskab og teknik til modellering og beregning.
- I økonomi og erhvervsliv til optimering, statistik og risikovurdering.
- I datalogi til algoritmer, kryptering og maskinlæring.
- I arkitektur og byggeri til strukturel analyse og præcisionsmålinger.
Moderne værktøjer som lommeregnere, computeralgebrasystemer (CAS), programmeringssprog (fx Python, R) og interaktive programmer (fx GeoGebra) gør det lettere at eksperimentere med og visualisere matematiske ideer.
Hvordan man lærer og arbejder med matematik
Effektiv matematikindlæring bygger på:
- Øvelse: gentagne opgaver for at opbygge færdigheder.
- Forståelse frem for memorering: prøv at se hvorfor regler gælder, ikke kun hvordan de bruges.
- Visualisering: tegninger, grafer og modeller hjælper med at gøre abstrakte ideer konkrete.
- Trinvise forklaringer: del komplekse problemer op i mindre skridt.
- Samarbejde og spørgsmål: diskussion med lærere eller medstuderende kan åbne nye forståelser.
Matematik er både et praktisk redskab og en måde at tænke klart og præcist på. Uanset om man bruger det i dagligdagen, i sit arbejde eller i forskning, giver matematik redskaber til at analysere, modellere og løse problemer.
Problemløsning i matematik
Matematik løser problemer ved hjælp af logik. Et af de vigtigste logiske værktøjer, som matematikere bruger, er deduktion. Deduktion er en særlig måde at tænke på, hvorpå man kan opdage og bevise nye sandheder ved hjælp af gamle sandheder. For en matematiker er grunden til, at noget er sandt (kaldet et bevis) lige så vigtig som det faktum, at det er sandt, og denne grund findes ofte ved hjælp af deduktion. At bruge deduktion er det, der adskiller matematisk tænkning fra andre former for videnskabelig tænkning, som kan være baseret på eksperimenter eller interviews.
Logik og ræsonnement bruges af matematikere til at skabe generelle regler, som er en vigtig del af matematikken. Disse regler udelader oplysninger, der ikke er vigtige, så en enkelt regel kan dække mange situationer. Ved at finde generelle regler løser matematikken mange problemer på samme tid, da disse regler kan bruges på andre problemer. Disse regler kan kaldes teoremer (hvis de er blevet bevist) eller formodninger (hvis man endnu ikke ved, om de er sande). De fleste matematikere bruger ikke-logiske og kreative ræsonnementer for at finde et logisk bevis.
Nogle gange finder og undersøger matematikken regler eller idéer, som vi endnu ikke forstår. I matematikken vælges ofte idéer og regler, fordi de anses for enkle eller pæne. På den anden side findes disse idéer og regler nogle gange i den virkelige verden, efter at de er blevet studeret i matematik; det er sket mange gange tidligere. Generelt kan studier af matematikkens regler og idéer hjælpe os med at forstå verden bedre. Nogle eksempler på matematiske problemer er addition, subtraktion, multiplikation, division, regning, brøker og decimaltal. Algebraproblemer løses ved at evaluere visse variabler. En lommeregner besvarer alle matematiske problemer i de fire grundlæggende aritmetiske operationer.
Studieområder inden for matematik
Nummer
Matematik omfatter studiet af tal og mængder.Det er en gren af videnskaben, der beskæftiger sig med logik i form, mængde og arrangement. De fleste af de områder, der er anført nedenfor, studeres inden for mange forskellige områder af matematikken, herunder mængdelære og matematisk logik. Studiet af talteori fokuserer normalt mere på de hele tals struktur og opførsel end på selve grundlaget for tal, og er derfor ikke opført i dette underafsnit.
| 0 , 1 , 2 , 2 , 3 , ... {\displaystyle 0,1,2,3,\ldots } | ... , - 1 , 0 , 0 , 1 , ... {\displaystyle \ldots ,-1,0,1,\ldots } | 1 2 , 2 3 , 0,125 , ... {\displaystyle {\frac {\frac {1}{2}}},{\frac {2}{3}}},0,125,\ldots } | π , e , 2 , ... {\displaystyle \pi ,e,{\sqrt {2}},\ldots } | 1 + i , 2 e i π / 3 , ... {\displaystyle 1+i,2e^{i\pi /3},\ldots } |
| Naturlige tal | Hele tal | Rationale tal | ||
| 0 , 1 , ... , ω , ω + 1 , ... , 2 ω , ... {\displaystyle 0,1,\ldots ,\omega ,\omega ,\omega +1,\ldots ,2\omega ,\ldots } | ℵ 0 , ℵ 1 , ... {\displaystyle \aleph _{0},\aleph _{1},\ldots } | + , - , × , ÷ {\displaystyle +,-,\times ,\div } | > , ≥ , = , ≤ , < {\displaystyle >,\geq ,=,\leq ,< } | f ( x ) = x {\displaystyle f(x)={\sqrt {x}}} |
| Ordinale tal | Kardinalnumre | Aritmetiske operationer | Aritmetiske forhold |
Struktur
Mange områder af matematikken undersøger den struktur, som et objekt har. De fleste af disse områder er en del af studiet af algebra.
|
|
|
|
|
|
| Talteori | Abstrakt algebra | Lineær algebra | Ordensteori |
Form
Nogle områder af matematikken undersøger tingenes form. De fleste af disse områder er en del af studiet af geometri.
|
|
|
|
|
|
| Topologi | Differentialgeometri |
Ændre
Nogle områder af matematikken undersøger den måde, hvorpå ting ændrer sig. De fleste af disse områder er en del af studiet af analyse.
|
|
|
|
| Vektorregning | ||
|
|
|
|
| Dynamiske systemer |
Anvendt matematik
Anvendt matematik bruger matematik til at løse problemer inden for andre områder som f.eks. teknik, fysik og datalogi.
Numerisk analyse - optimering - sandsynlighedsregning - statistik - matematisk finansiering - spilteori - matematisk fysik - væskedynamik - beregningsalgoritmer
Berømte teoremer
Disse sætninger har interesseret både matematikere og folk, der ikke er matematikere.
Pythagoras sætning - Fermats sidste sætning - Goldbachs formodning - Twin Prime-sætningen - Gödels ufuldstændighedssætninger - Poincaré-sætningen - Cantors diagonalargument - Firefarvetesætningen - Zorns lemma - Eulers identitet - Church-Turing-tesen
Det er teoremer og formodninger, der har ændret matematikken i høj grad.
Riemann-hypotesen - Kontinuumshypotesen - P versus NP - Pythagoras' sætning - Central grænsesætning - Grundlæggende sætning i regning - Grundlæggende sætning i algebra - Grundlæggende sætning i aritmetik - Grundlæggende sætning i projektiv geometri - klassifikationssætninger for overflader - Gauss-Bonnet-sætning - Fermats sidste sætning - Kantorovich-sætningen
Grundlag og metoder
Fremskridt i forståelsen af matematikkens natur har også indflydelse på den måde, som matematikere studerer deres fag på.
Matematikfilosofi - Matematisk intuitionisme - Matematisk konstruktivisme - Matematikkens grundlag - Mængdelære - Symbolsk logik - Modelteori - Kategoriteori - Logik - Omvendt matematik - Tabel over matematiske symboler
Historie og matematikerens verden
Matematik i historien og matematikkens historie.
Matematikkens historie - Matematikkens tidslinje - Matematikere - Fields medaljen - Abel-prisen - Millennium Prize Problems (Clay MathPrize) - International Mathematical Union - Matematikkonkurrencer - Lateral tænkning - Matematik og køn
Priser i matematik
Der findes ingen Nobelpris i matematik. Matematikere kan modtage Abel-prisen og Fields Medaljen for vigtige værker.
Clay Mathematics Institute har sagt, at det vil give en million dollars til den, der løser et af millenniumprisproblemerne.
Matematiske værktøjer
Der er mange værktøjer, der bruges til at lave matematik eller til at finde svar på matematiske problemer.
Ældre værktøjer
Nyere værktøjer
- lommeregnere og computere
- Programmeringssprog
- Computer algebra systemer (liste)
- Internet-betegnelse
- software til statistisk analyse (f.eks. SPSS)
- SAS-programmeringssprog
- programmeringssproget R
Se også
- Tidslinje for kvinder i matematik
- Amerikansk matematisk selskab
- Selskab for industriel og anvendt matematik
- Matematik-slægtsforskningsprojekt
- Matematik emneklassifikation
Spørgsmål og svar
Spørgsmål: Hvad er matematik?
A: Matematik er studiet af tal, former og mønstre. Ordet kommer fra det græske μάθημα (máthema), der betyder "videnskab, viden eller lærdom".
Q: Hvad er de vigtigste områder inden for matematik?
A: Matematikkens hovedområder omfatter tal, struktur (algebra), sted (geometri) og forandring (analyse).
Spørgsmål: Hvordan bruges matematik i den virkelige verden?
A: Anvendt matematik er nyttig til løsning af problemer i den virkelige verden. Folk, der arbejder i erhvervslivet, inden for videnskab, teknik og byggeri, bruger matematik.
Spørgsmål: Findes der en forkortet version af "matematik"?
A: Ja - det kan forkortes til "maths" i de britiske Commonwealth-lande eller "math" i Nordamerika.
Spørgsmål: Hvad betyder ordet "matematik"?
A: Ordet "matematik" kommer fra græsk μάθημα (máthema), der betyder "videnskab, viden eller lærdom".
Spørgsmål: Hvilken type problemløsning indebærer anvendt matematik?
A: Anvendt matematik indebærer løsning af problemer i den virkelige verden, som folk, der arbejder inden for erhvervsliv, videnskab, ingeniørvidenskab og byggeri, står over for.
Søge