Hvad er fraktaler? Definition, eksempler og anvendelser
Opdag fraktaler: klar definition, visuelle eksempler og praktiske anvendelser indenfor natur, teknologi og kunst. Lær hvordan selv-lignende mønstre former verden.
En fraktal er et mønster, der, når det ses som et billede, giver et billede, som, når der zoomes ind, stadig giver det samme billede. Det kan skæres i dele, der ligner en mindre udgave af det billede, der blev startet med. Ordet fraktal blev lavet af Benoît Mandelbrot i 1975 af det latinske ord fractus, som betyder "brudt" eller "splittet". Et simpelt eksempel er et træ, der forgrener sig i mindre grene, og disse grene i mindre grene osv. Fraktaler er ikke kun smukke, men har også mange praktiske anvendelser.
Egenskaber ved fraktaler
- Selv‑similaritet: Delene ligner helheden — enten præcist (eksakte fraktaler) eller statistisk (nogle naturlige fraktaler).
- Skala‑uafhængighed: Mønstret gentager sig på forskellige skalaer; ved zoom ændres struktur ikke grundlæggende.
- Kompleksitet fra simple regler: Mange fraktaler opstår ved gentagen anvendelse af en simpel regel eller transformation.
- Fraktal dimension: Fraktaler har ofte en ikke‑heltal dimension, som beskriver hvor "tæt" de fylder rummet (f.eks. Koch‑kurvens dimension ≈ 1,26).
- Uendelig detalje: Matematiske fraktaler kan indeholde detaljer på alle skalaer; fysiske fraktaler er dog begrænset af materiens atomare skala.
Matematiske og naturlige eksempler
- Matematiske: Mandelbrot‑mængden og Julia‑mængderne (komplekse, iterative sæt), Sierpinski‑trekanten, Koch‑snefnug og Cantor‑mængden.
- Naturlige: Kystlinjer, skyer, bjerglandskaber, floddeltaer, plantestrukturer (grenmønstre), blodkar og lungeblærer — disse viser ofte statistisk selv‑similaritet.
- En simpel illustration: Tænk på et træ, der forgrener sig i mindre grene; hver gren ligner hele træet i struktur.
Hvordan genereres fraktaler?
Fraktaler skabes typisk ved gentagne (iterative) procedurer. Nogle almindelige metoder:
- Itererede funktioner: Man anvender samme matematiske transformation igen og igen (fx ved komplekse tal for Mandelbrot/Julia).
- IFS — Iterated Function Systems: En samling af affine transformationer, anvendt tilfældigt eller systematisk for at bygge fraktalen.
- L‑systemer: Regelsæt der bruges til at modellere plantevækst og andre forgreningsstrukturer.
- Escape‑time algoritmer: Bestemmer, hvor hurtigt punkter "flygter" under iteration, og farver dem for at skabe billeder af fraktaler.
- Stokastiske metoder: Tilføjelse af tilfældighed (fx random midpoint displacement) for at modellere naturlige, ru overflader.
Fraktal dimension — et kort indblik
Fraktal dimension kvantificerer, hvor meget et fraktalmønster fylder i forhold til den skala, det betragtes i. For selv‑simile fraktaler gælder ofte formlen:
D = log(N) / log(s)
hvor N er antallet af lignende dele og s er skalafaktoren. Eksempel: Koch‑kurven består af 4 dele hver med 1/3 af længden, så D = log(4)/log(3) ≈ 1,2619. Dimensionen ligger derfor mellem heltallene for topologisk dimension (fx mellem 1 og 2).
Anvendelser
- Computer‑grafik og film: Fraktaler bruges til at skabe realistiske landskaber, teksturer og skyer.
- Signal‑ og billedbehandling: Fraktalbaserede metoder anvendes i kompression og mønstergenkendelse.
- Telekommunikation: Fraktalantenner giver gode flerbands‑egenskaber på lille plads.
- Medicin og biologi: Modellering af blodkarsnetværk, lunger og vækstmønstre; analyse af uregelmæssigheder i biologiske strukturer.
- Geovidenskab og meteorologi: Modellering af kystlinjer, flodsystemer, skyer og turbulens.
- Økonomi og statistik: Fraktalgeometri og selv‑lignende processer bruges i analyser af finansielle tidsserier (med forsigtighed).
- Kunst og design: Fraktale former inspirerer grafik, arkitektur og mønsterdesign.
Begrænsninger og misforståelser
- Ikke alle gentagne eller komplekse mønstre er strengt matematiske fraktaler; mange naturlige objekter viser kun statistisk selv‑similaritet over et begrænset skalaområde.
- Matematiske fraktaler har uendelig detalje, men i praktiske anvendelser er der altid fysiske begrænsninger (måleskala, pixels, atomær struktur).
- Anvendelser som finansielle modeller kræver forsigtighed — naturen af stokastisk data er ikke altid godt beskrevet alene ved fraktal teori.
Fraktaler forbinder matematik, natur og kunst på en unik måde: simple regler kan give komplekse, ofte smukke strukturer, og forståelsen af fraktaler hjælper både med æstetiske billeder og praktiske problemstillinger inden for videnskab og teknologi.
En Sierpinski-triangel efter 7 gentagelser.
Mandelbrot-mængden er et berømt eksempel på en fraktal.
Eksempler
Der findes mange typer fraktaler, som er lavet på mange forskellige måder. Et eksempel er Sierpinski-trekanten, hvor der er et uendeligt antal små trekanter inden for den store trekant. Et andet eksempel er Mandelbrot-mængden, der er opkaldt efter Benoît Mandelbrot. Sierpinksi-trekanten er konstrueret ved hjælp af mønstre, men Mandelbrot-mængden er baseret på en ligning.
Der er også mange naturlige eksempler på fraktaler i naturen, herunder træer, snefnug, visse grøntsager og kystlinjer.
Koch-kurven
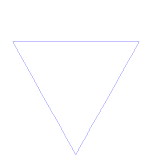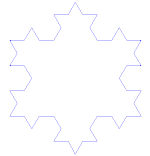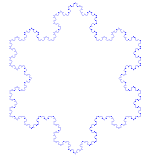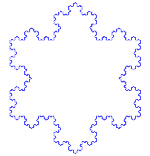
Koch-kurven er et simpelt eksempel på en fraktal. Først starter vi med en del af en lige linje - kaldet et retlinjesegment. Skær linjen i 3 stykker af samme størrelse. Fjern den midterste af disse stykker, og sæt den øverste del af en trekant ind med sider, der er lige lange som den del, der skal skæres ud. Vi har nu 4 linjestykker, som berører hinanden i enderne. Vi kan nu gøre det, som vi lige har gjort med det første segment, med hver af de 4 stykker. Vi kan nu gøre det samme igen og igen med alle de stykker, vi får. Vi gør nu dette for evigt og ser, hvad vi ender med.
Længden af Koch-kurven er uendelig, og arealet af Koch-kurven er nul. Dette er ret mærkeligt. Et linjestykke (med dimension 1) kan have en længde på 1, men det har et areal på 0. Et kvadrat med længde 1 og bredde 1 (med dimension 2) vil have areal 1 og længde uendelig.
Dimensionen lighed
Koch-kurven synes altså at være større end noget af dimension 1 og mindre end noget af dimension 2. Ideen med lighedsdimensionen er at give en dimension, som giver en bedre idé om længde eller areal for fraktaler. Så for en Koch-kurve ønsker vi en dimension mellem 1 og 2.
Koch-kurven kan skæres i fire stykker, som hver er 1 3 {\displaystyle {\frac {1}{3}}}}
af størrelsen af originalen. Vi kalder antallet af stykker, som en fraktal kan skæres i, for N {\displaystyle N}
, og vi kalder størrelsesforskellen B {\displaystyle B}
. Vi sætter dem ind i ligningen:
log N - log B {\displaystyle {\frac {\log N}{-\log B}}} 
Hvor log {\displaystyle \log } er 
logaritmen af et tal. Dette tal er fraktalens Hausdorff-dimension. I Koch-kurven er dette log 4 - log 1 3 = 1,2619... {\displaystyle {\frac {\log 4}{-\log {\frac {\frac {1}{3}}}}=1,2619... }
som vi ønskede.
Koch-kurven er en af de enkleste fraktalformer, og derfor er dens dimension let at beregne. Dens similaritetsdimension og Hausdorff-dimension er begge ens. Dette gælder ikke for mere komplekse fraktaler.
Koch snefnug
Koch-snefnuget (eller Koch-stjernen) er det samme som Koch-kurven, bortset fra at det starter med en ligesidet trekant i stedet for et linjestykke.
Sådan laver du Koch-kurven
Bruger
Fraktaler har mange anvendelsesmuligheder, f.eks. inden for biologi (lunge, nyrer, hjerterytmevariabilitet osv.), jordskælv, finanssektoren, hvor de er relateret til de såkaldte tunge halefordelinger, og inden for fysik. Dette tyder på, at fraktaler bør studeres for at forstå, hvorfor fraktaler er så hyppige i naturen.Nogle fraktaler findes kun af kunstneriske årsager, men andre er meget nyttige. Fraktaler er meget effektive former for radioantenner og bruges i computerchips til effektivt at forbinde alle komponenterne. Kystlinjer kan også betragtes som fraktaler.
Spørgsmål og svar
Q: Hvad er en fraktal?
A: En fraktal er et mønster, der, når det ses som et billede, producerer et billede, der stadig vil lave det samme billede, når der zoomes ind på det.
Q: Hvem er krediteret for at have opfundet udtrykket "fraktal"?
A: Benoît Mandelbrot er krediteret for at have opfundet udtrykket "fraktal" i 1975.
Q: Hvad er etymologien bag ordet "fraktal"?
A: Ordet "fraktal" er afledt af det latinske ord "fractus", som betyder "brudt" eller "brudt".
Q: Kan fraktaler skæres i dele?
A: Ja, fraktaler kan skæres i dele, der ligner en mindre version af det billede, de startede med.
Q: Kan du give et eksempel på en fraktal?
A: Et simpelt eksempel på en fraktal er et træ, der forgrener sig i mindre grene, og disse grene forgrener sig i mindre grene og så videre.
Q: Hvilke praktiske anvendelser har fraktaler?
A: Fraktaler har mange praktiske anvendelser, f.eks. inden for computergrafik, medicin, fysik og finans.
Q: Hvorfor er fraktaler vigtige?
A: Fraktaler er vigtige, fordi de kan hjælpe os med at forstå komplekse naturfænomener og skabe mere nøjagtige modeller og simuleringer.
Søge