AlegsaOnline.com

Pythagoras' sætning: Definition og bevis for retvinklede trekanter

Lær Pythagoras' sætning: definition, formel a^2+b^2=c^2, hypotenuse, trinvis bevis og eksempler for retvinklede trekanter.

Forfatter: Leandro Alegsa

29-01-2026

I matematik er Pythagoras' sætning eller Pythagoras' sætning et udsagn om siderne i en retvinklet trekant.

En af vinklerne i en retvinklet trekant er altid lig med 90 grader. Denne vinkel er den rette vinkel. De to sider ved siden af den rette vinkel kaldes benene, og den anden side kaldes hypotenusen. Hypotenusen er den side, der er modsat den rette vinkel, og det er altid den længste side.

Definition og formel

Pythagoras' sætning siger, at i en retvinklet trekant med benlængderne a og b og hypotenusen c gælder:

a² + b² = c²

Her er a og b længderne af de to ben (de to sider, der mødes i den rette vinkel) og c længden af hypotenusen. Denne lighed forbinder kvadraterne på siderne: kvadratet på hypotenusen er summen af kvadraterne på de to ben.

Et simpelt geometrisk bevis (omrokering)

Et velkendt og letfatteligt bevis bruger en kvadratisk figur, der består af fire kongruente retvinklede trekanter og et centralt kvadrat:

Tag fire ens retvinklede trekanter med ben a og b og hypotenuse c og læg dem i et kvadrat med side (a + b).
Det store kvadrats areal er (a + b)² = a² + 2ab + b².
Inde i det store kvadrat ligger fire trekanter (samlet areal 4·(1/2ab) = 2ab) og i midten et mindre kvadrat med side c (areal c²).
Dermed er (a + b)² = 2ab + c². Ved at reducere får man a² + b² = c².

Bevis ved ligedannede trekanter

Et andet klassisk bevis bruger ligedannede trekanter ved at sænke en højde fra den rette vinkel ned på hypotenusen. Højden deler hypotenusen i to stykker d og e (så d + e = c). Ved ligedannende forhold fås

a² = c·d og b² = c·e.

Summation giver a² + b² = c(d + e) = c·c = c².

Konversen

Konversen til Pythagoras' sætning siger: hvis i en trekant med sider a, b og c gælder a² + b² = c², så er vinklen overfor siden c en ret vinkel. Et kort bevis bruger for eksempel cosinusrelationen (cosinus af vinklen er nul når summen af kvadraterne passer), hvilket viser at vinklen er 90°.

Eksempler og pythagoræiske tripler

Den mest kendte numeriske anvendelse er 3² + 4² = 9 + 16 = 25 = 5², altså en 3-4-5-trekant.
Andre kendte primære tripler er 5-12-13 og 8-15-17. Et generelt sæt primitive pythagoræiske tripler kan fremstilles ved for heltal m > n > 0 (m og n ikke begge lige) ved formlerne: a = m² − n², b = 2mn, c = m² + n².

Anvendelser

Pythagoras' sætning bruges i mange sammenhænge:

Til at beregne afstande i geometri og i koordinatgeometri (afstand mellem to punkter i planen følger direkte af sætningen).
I praktiske bygge- og opmålingsopgaver for at sikre rette vinkler (fx brug af 3-4-5-reglen).
I trigonometrien som grundlag for definitioner og relationer mellem sider og vinkler.
I vektorregning og analytisk geometri underbygger den euklidiske længdemåling (normen) i det flerdimensionale rum.

Generaliseringer og bemærkninger

Lov om cosinus er en naturlig generalisering: c² = a² + b² − 2ab cos(γ). Når γ = 90° forsvinder sidste led, og man får Pythagoras' sætning.
I n-dimensioner anvendes en tilsvarende sum af kvadrater til at bestemme afstand (f.eks. i R³: d² = x² + y² + z²).
Pythagoras' sætning er kernen i mange områder af matematik og fysik, og der findes hundredevis af forskellige beviser — både algebraiske, geometriske og analytiske.

Kort historisk note

Sætningen er opkaldt efter Pythagoras af Samos, men kendskab til forholdet mellem siderne i retvinklede trekanter kendes også fra ældre civilisationer som babylonerne og egypterne. Pythagoræerne lagde navn til og formulerede en række bevise og anvendelser, der har givet sætningen dens klassiske status.

Hvis du vil have et trin-for-trin-regneeksempel (fx hvordan man udregner hypotenusen eller et ben givet de andre sider), så sig til — jeg viser gerne et regneeksempel.

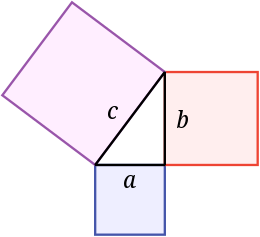
Pythagoras sætning Summen af arealerne af de to kvadrater på benene (a og b) er lig med arealet af kvadratet på hypotenusen (c).

Teoriens påstand

Den pythagoræiske sætning siger, at arealet af et kvadrat på hypotenusen er lig med summen af arealerne af kvadraterne på benene. I dette billede er arealet af det blå kvadrat lagt sammen med arealet af det røde kvadrat og udgør arealet af det lilla kvadrat. Det blev opkaldt efter den græske matematiker Pythagoras:

Hvis længden af benene er a og b, og længden af hypotenusen er c, så er a 2 + b 2 = c 2 {\displaystyle a^{2}+b^{2}=c^{2}}} $a^{2}+b^{2}=c^{2}$ .

Typer af beviser

Der findes mange forskellige beviser for denne sætning. De falder i fire kategorier:

De, der er baseret på lineære relationer: de algebraiske beviser.
De geometriske beviser er baseret på sammenligning af arealer.
De, der er baseret på vektoroperation.
Dem, der er baseret på masse og hastighed: de dynamiske beviser.

Bevis

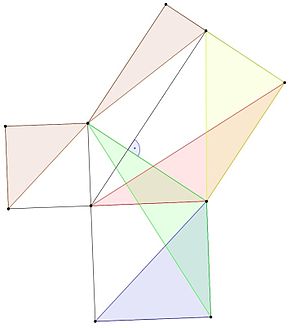
Et af beviserne for Pythagoras' sætning blev fundet af den græske matematiker Eudoxus af Cnidus.

Beviset er baseret på tre lemmaer:

Trekanter med samme grundflade og højde har samme areal.
En trekant, der har samme grundflade og højde som en side af et kvadrat, har samme areal som halvdelen af kvadratet.
Trekanter med to kongruente sider og en kongruent vinkel er kongruente og har samme areal.

Beviset er:

Den blå trekant har samme areal som den grønne trekant, fordi den har samme grundflade og højde (lemma 1).
Grønne og røde trekanter har begge to sider, der er lig med siderne i de samme kvadrater, og en vinkel, der er lig med en lige vinkel (en vinkel på 90 grader) plus en trekantvinkel, så de er kongruente og har samme areal (lemma 3).
De røde og gule trekants arealer er lige store, fordi de har samme højde og basis (lemma 1).
Den blå trekants areal er lig med arealet af den gule trekants areal, fordi

A b l u e = A g r e e n = A r e d = A y e l l o w {\displaystyle {\color {\blue}A_{blue}}}={\color {green}A_{green}}}={\color {red}A_{red}}={\color {yellow}A_{yellow}}} ${\color {blue}A_{blue}}={\color {green}A_{green}}={\color {red}A_{red}}={\color {yellow}A_{yellow}}$

De brune trekanter har samme areal af samme grund.
Blå og brun har hver et halvt så stort areal som et mindre kvadrat. Summen af deres arealer er lig med halvdelen af arealet af det større kvadrat. Derfor er halvdelen af arealerne af små kvadrater det samme som halvdelen af arealet af det større kvadrat, så deres areal er det samme som arealet af det større kvadrat.

Bevis ved hjælp af lignende trekanter

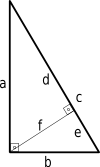
Vi kan få et andet bevis for Pythagoras sætning ved at bruge lignende trekanter.

d a = a c ⇒ a 2 = d c ( 1 ) {\displaystyle {\frac {\frac {d}{a}}}={\frac {a}{c}}}\quad \Rightarrow \quad {a^{2}}}={dc}\quad (1)} ${\frac {d}{a}}={\frac {a}{c}}\quad \Rightarrow \quad {a^{2}}={dc}\quad (1)$

e b = b c ⇒ b 2 = e c ( 2 ) {\displaystyle {\frac {\frac {e}{b}}}={\frac {b}{c}}}\quad \Rightarrow \quad {b^{2}}}={ec}\quad (2)} ${\frac {e}{b}}={\frac {b}{c}}\quad \Rightarrow \quad {b^{2}}={ec}\quad (2)$

Ud fra billedet tilføjes ligningerne (1) og (2):

a 2 + b 2 = d c + e c ⇒ a 2 + b 2 = c ( d + e ) ⇒

${a^{2}}+{b^{2}}={dc+ec}\quad \Rightarrow a^{2}+b^{2}=c(d+e)\quad \Rightarrow a^{2}+b^{2}=c(c)$

Og vi får:

c 2 = a 2 + b 2 . {\displaystyle c^{2}=a^{2}+b^{2}\,\!.} $c^{2}=a^{2}+b^{2}\,\!.$

Pythagoræiske tripler

Pythagoræiske tripler eller tripletter er tre hele tal, som passer til ligningen a 2 + b 2 = c 2 {\displaystyle a^{2}+b^{2}=c^{2}} $a^{2}+b^{2}=c^{2}$ .

Trekanten med siderne 3, 4 og 5 er et velkendt eksempel. Hvis a=3 og b=4, så er 3 2 + 4 2 = 5 2 {\displaystyle 3^{2}+4^{2}=5^{2}}} $3^{2}+4^{2}=5^{2}$ fordi 9 + 16 = 25 {\displaystyle 9+16=25} $9+16=25$ . Dette kan også vises som 3 2 + 4 2 = 5. {\displaystyle {\sqrt {3^{2}+4^{2}}}=5.} ${\sqrt {3^{2}+4^{2}}}=5.$

Tre-fire-fem-trekanten fungerer for alle multipla af 3, 4 og 5. Med andre ord er tal som 6, 8, 10 eller 30, 40 og 50 også pythagoræiske tripler. Et andet eksempel på en triangel er 12-5-13 trekanten, fordi 12 2 + 5 2 = 13 {\displaystyle {\sqrt {12^{{2}+5^{2}}}}=13} ${\sqrt {12^{2}+5^{2}}}=13$ .

En pythagoræisk tripel, som ikke er et multiplum af andre tripper, kaldes en primitiv pythagoræisk tripel. Enhver primitiv pythagoræisk tripel kan findes ved hjælp af udtrykket ( 2 m n , m 2 - n 2 , m 2 + n 2 ) {\displaystyle (2mn,m^{2}-n^{2},m^{2}+n^{2})} $(2mn,m^{2}-n^{2},m^{2}+n^{2})$ , men følgende betingelser skal være opfyldt. De begrænser værdierne for m {\displaystyle m} og n {\displaystyle n} .

m {\displaystyle m} og n {\displaystyle n} er positive hele tal
m {\displaystyle m} og n {\displaystyle n} har ingen fælles faktorer undtagen 1
m {\displaystyle m} og n {\displaystyle n} har modsat paritet. m {\displaystyle m} og n {\displaystyle n} har modsat paritet, når m {\displaystyle m} er lige og n {\displaystyle n} er ulige, eller m {\displaystyle m} er ulige og n {\displaystyle n} er lige.
m > n {\displaystyle m>n} $m>n$ .

Hvis alle fire betingelser er opfyldt, danner værdierne af m {\displaystyle m} og n {\displaystyle n} en primitiv pythagoræisk tripel.

m = 2 {\displaystyle m=2} $m=2$ og n = 1 {\displaystyle n=1} $n=1$ skaber en primitiv pythagoræisk tripel. Værdierne opfylder alle fire betingelser. 2 m n = 2 × 2 × 1 = 4 {\displaystyle 2mn=2\times 2\times 2\times 1=4} $2mn=2\times 2\times 1=4$ , m 2 - n 2 2 = 2 2 2 - 1 2 = 4 - 1 = 3 {\displaystyle m^{2}-n^{2}=2^{2}-1^{2}=4-1=3} $m^{2}-n^{2}=2^{2}-1^{2}=4-1=3$ og m 2 + n 2 2 = 2 2 2 + 1 2 = 4 + 1 = 5 {\displaystyle m^{2}+n^{2}=2^{2}+1^{2}=4+1=5} $m^{2}+n^{2}=2^{2}+1^{2}=4+1=5$ , så triplen ( 3 , 4 , 5 ) {\displaystyle (3,4,5)} $(3,4,5)$ er dannet.

Spørgsmål og svar

Spørgsmål: Hvad er den pythagoræiske sætning?

A: Den pythagoræiske sætning er et udsagn om siderne i en retvinklet trekant.

Spørgsmål: Hvilken vinkel er altid lig med 90 grader i en retvinklet trekant?

Svar: En af vinklerne i en retvinklet trekant er altid lig med 90 grader, hvilket kaldes den rette vinkel.

Spørgsmål: Hvad hedder de to sider ved siden af den rette vinkel?

A: De to sider ved siden af den rette vinkel kaldes benene.

Spørgsmål: Hvad hedder den side, der ligger over for den rette vinkel?

A: Den side, der er modsat den rette vinkel, kaldes hypotenusen, og det er altid den længste side.

Spørgsmål: Er der en ligning til at beregne denne sætning?

A: Ja, der findes en ligning til beregning af denne sætning, som siger, at "kvadratet på længden af hypotenusen er lig med summen af kvadraterne af længderne af de to andre sider".

Spørgsmål: Er alle trekanter med 90 graders vinkler "retvinklede" trekanter?

A: Nej, ikke alle trekanter med 90 graders vinkler betragtes som "rette" trekanter; kun de trekanter, hvor den ene side (hypotenusen) er længere end de to andre sider og danner en 90 graders vinkel i sin ende, kan klassificeres som "rette" trekanter.