Funktion (matematik)

I matematik er en funktion et matematisk objekt, der producerer et output, når det får et input (som kan være et tal, en vektor eller hvad som helst, der kan eksistere i et sæt af ting).

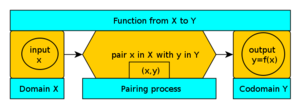
En funktion er altså som en maskine, der tager en værdi x og returnerer et output y. Mængden af alle værdier, som x kan have, kaldes domænet, og mængden, der indeholder alle de værdier, som y kan have, kaldes kodomænet. En funktion betegnes ofte med kursive bogstaver som f {\displaystyle f} , g {\displaystyle g} , h {\displaystyle h} $h$ .

Hvis dette sker, siger vi, at y er en funktion af x, og vi skriver y = f ( x ) {\displaystyle y=f(x)} $y=f(x)$ . Her er f {\displaystyle f} navnet på funktionen, og man skriver f : X → Y {\displaystyle f:X\til Y} (funktion fra X til Y) for at repræsentere de tre dele af funktionen: domænet (X), kodomænet (Y) og parringsprocessen (pilen).

Et eksempel på en funktion er f ( x ) = x + 1 {\displaystyle f(x)=x+1} $f(x)=x+1$ . Man giver et naturligt tal x {\displaystyle x} som input og får et naturligt tal y {\displaystyle y} , som er x + 1 {\displaystyle x+1} $x+1$ . Hvis man f.eks. giver 3 som input til f {\displaystyle f} , får man f.eks. 4 som output.

En funktion behøver ikke nødvendigvis at være en ligning. Hovedidéen er, at input og output skal parres sammen på en eller anden måde - også selv om processen kan være meget kompliceret.

Metaforer

Tabeller

Ind- og uddata kan anbringes i en tabel som på billedet; det er nemt, hvis der ikke er for mange data.

Grafer

På billedet kan man se, at både 2 og 3 er blevet parret med c; dette er ikke tilladt i den anden retning, da 2 ikke kan udstede c og d på samme tid (hvert input kan kun have ét output). Alle f ( x ) {\displaystyle f(x)} f(x) (c og d på billedet) kaldes normalt for billedmængden af f {\displaystyle f} , og billedmængden kan være hele kodomænet eller en af dets delmængder. Man kan sige, at billedmængden af en delmængde A af domænet er f(A). Hvis input og output har en rækkefølge, er det let at tegne dem på en graf:

På den måde kommer billedet på billedet af mængden A.

Historie

I 1690'erne brugte Gottfried Leibniz og Johann Bernoulli ordet "funktion" med bogstaver imellem sig, så det moderne begreb begyndte på samme tid som regning.

I 1748 gav Leonhard Euler følgende definition på en funktion:

"En funktion af en variabel størrelse er et analytisk udtryk, der på en hvilken som helst måde er sammensat af den variable størrelse og tal eller konstante størrelser."

og derefter i 1755:

"Hvis nogle størrelser er så afhængige af andre størrelser, at hvis sidstnævnte ændres, ændres førstnævnte også, kaldes førstnævnte størrelser for funktioner af sidstnævnte. Denne definition gælder ret bredt og omfatter alle måder, hvorpå en størrelse kan være bestemt af andre. Hvis x derfor betegner en variabel størrelse, så kaldes alle størrelser, som på nogen måde afhænger af x eller bestemmes af x, for funktioner af x."

Peter Dirichlet er normalt krediteret for den første moderne definition af en funktion (formuleret i 1837). Den blev ofte brugt i skoler indtil anden halvdel af det 20. århundrede:

"y er en funktion af en variabel x, defineret på intervallet a < x < b, hvis der til enhver værdi af variablen x i dette interval svarer en bestemt værdi af variablen y. Det er også irrelevant, hvordan denne korrespondance er etableret."

I 1939 generaliserede Bourbaki Dirichlet-definitionen og gav en mængdeteoretisk version af definitionen som en korrespondance mellem input og output; dette blev brugt i skolerne fra omkring 1960.

Endelig gav Bourbaki i 1970 den moderne definition som en tripel f = ( X , Y , F ) {\displaystyle f=(X,Y,F)} , med F ⊂ X × Y , ( x , f ( x ) ) ∈ $F\subset X\times Y,(x,f(x))\in F$ (dvs. f : X → Y {\displaystyle f:X\til Y} og F = { ( x , f ( x ) ) ∣ x ∈ X , f ( x ) ∈ $F=\{(x,f(x))\mid x\in X,f(x)\in Y\}$ ). $X$ kaldes $f's$ domæne, $Y$ dens kodomæne og $F$ dens graf. Mængden af alle elementer af formen $f (x)$ , hvor $x$ spænder over elementerne i domænet $X$ , kaldes billedet af $f$ . Billedet af en funktion er en delmængde af dens kodomæne og er muligvis ikke sammenfaldende med dette.

Typer af funktioner

Elementære funktioner - De funktioner, der normalt studeres i skolen: brøker, kvadratrødder, sinus-, cosinus- og tangentfunktionen og nogle andre funktioner.
Ikke-elementære funktioner - De fleste af dem bruger operationer, som vi ikke lærer i skolen (som + eller - eller potenser). Mange integraler er f.eks. ikke elementære.
Inverse funktioner - Funktioner, der ophæver en anden funktion. For eksempel: Hvis F(x) er den omvendte af f(x)=y, så er F(y)=x. Ikke alle funktioner har inverser.
Særlige funktioner: Funktioner, der har navne. Disse omfatter trigonometriske funktioner såsom sinus, cosinus og tangens. Funktioner som f(x)=3x (tre gange x) kaldes ikke specielle funktioner. Særlige funktioner kan være elementære, ikke-elementære eller inverser.

Relaterede sider

Konstant funktion
Kontinuerlig funktion
Funktionssammensætning
Særlige funktioner

Gamma-funktion
Matrix-funktion

Lineær funktion
Lucy Joan Slater - britisk matematiker, der studerede matematiske funktioner
MATLAB, Wolfram Mathematica - software til at beregne matematiske funktioner
Relation (matematik)

Spørgsmål og svar

Spørgsmål: Hvad er en funktion i matematik?

Svar: En funktion i matematik er et objekt, der producerer et output, når der gives et input, som kan være et tal, en vektor eller hvad som helst, der kan eksistere inden for et sæt af ting.

Sp: Hvad er de to sæt, der er forbundet med funktioner?

Svar: Mængden af alle værdier, som x kan have, kaldes domænet, og den mængde, der indeholder alle værdier, som y kan have, kaldes kodomænet.

Spørgsmål: Hvordan betegnes funktioner ofte?

Svar: Funktioner betegnes ofte med kursiv skrift, f.eks. f, g, h.

Spørgsmål: Hvordan repræsenterer vi en funktion?

Svar: Vi repræsenterer en funktion ved at skrive y = f(x), hvor f er funktionens navn, og man skriver f : X → Y (funktion fra X til Y) for at repræsentere de tre dele af funktionen - domæne (X), kodomæne (Y) og parringsproces (pilen).

Spørgsmål: Kan du give et eksempel på en funktion?

Svar: Et eksempel på en funktion er f(x) = x + 1. Man giver et naturligt tal x som input og får det naturlige tal y, som er x + 1. Hvis man f.eks. giver 3 som input til f, får man 4 som output.

Spørgsmål: Skal alle funktioner være en ligning?

Svar: Nej, det er ikke alle funktioner, der behøver at være en ligning. Hovedidéen bag funktioner er, at input og output parres sammen på en eller anden måde - også selv om det kan være meget kompliceret.