Grafteori | et område af matematikken om grafer
Grafteori er et område af matematikken om grafer. En graf er en abstrakt repræsentation af: et antal punkter, der er forbundet med linjer. Hvert punkt kaldes normalt et toppunkt (flere punkter kaldes toppunkter), og linjerne kaldes kanter. Grafer er et værktøj til at modellere relationer. De bruges til at finde svar på en række problemer.
Nogle af disse spørgsmål er:
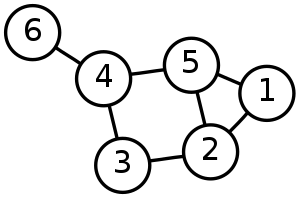
En ubestrøget graf.
Forskellige former for grafer
- Grafteori har mange aspekter. Grafer kan være dirigerede eller udirigerede. Et eksempel på en rettet graf er et vejsystem i en by. Nogle gader i byen er ensrettede gader. Det betyder, at der på disse strækninger kun er én retning at følge.
- Grafer kan være vægtede. Et eksempel er et vejnet med afstande eller med vejafgifter (for veje).
- Knuderne (cirklerne i skemaet) i en graf kaldes hjørner. De linjer, der forbinder knuderne, kaldes kanter. Der kan ikke være nogen linje mellem to knudepunkter, der kan være én linje, eller der kan være flere linjer.
- Inden for grafteori er strukturer i form af træer meget udbredte, de repræsenterer hierarkiske strukturer. Et træ er en rettet eller urettet graf, hvor der ikke er nogen cyklus, dvs. ingen mulighed for at gå fra et toppunkt (f.eks. en by) til det samme ved hjælp af hver kant, som man kun bruger én gang (man går kun én gang på hver vej, man tager).
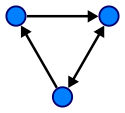
En rettet graf.
Historie
→
→ 
En visualisering af de syv broer i Königberg. Leonhard Euler løste dette problem i 1736, hvilket førte til udviklingen af topologi og moderne grafteori.
En graf er en abstrakt datastruktur. Den indeholder knuder, der normalt er relateret til hinanden. En knude er et datasæt, typisk i form af ordnede par. Knuder er enten forbundet eller ikke forbundet med en anden knude. Relationen mellem knuder defineres normalt som en kant. Grafer er nyttige på grund af deres evne til at forbinde knuder med andre knuder. Der findes et par repræsentationer af grafer i praksis.
Leonhard Euler boede i en by ved navn Königsberg. (Dens navn blev ændret til Kaliningrad i 1946). Byen ligger ved floden Pregel. Der er en ø i floden. Der er nogle broer over floden. Euler ville gerne gå rundt og bruge hver af broerne én gang. Han spurgte, om han kunne gøre dette. I 1736 udgav han en videnskabelig artikel, hvor han viste, at det ikke var muligt. I dag er dette problem kendt som de syv broer i Königsberg. Artiklen betragtes som den første artikel i grafteoriens historie.
Denne artikel, såvel som Vandermondes artikel om ridderproblemet, videreførte den analyse situs, som Leibniz havde indledt. Eulers formel var om antallet af kanter, hjørner og flader i et konvekst polyeder blev studeret og generaliseret af Cauchy og L'Huillier, og den ligger til grund for topologien.
Fusionen af ideer fra matematikken med ideer fra kemien er oprindelsen til en del af standardterminologien i grafteori. Især blev begrebet "graf" indført af Sylvester i en artikel offentliggjort i 1878 i Nature.
Et af de mest berømte og produktive problemer inden for grafteori er firefarveproblemet: "Er det sandt, at ethvert kort tegnet i planen kan have sine regioner farvet med fire farver på en sådan måde, at to regioner, der har en fælles grænse, har forskellige farver?"
Problemet med Königsbergbroen, på et bykort
Samme problem, men ved hjælp af en graf
Grafteori i perspektiv
Grafteori er en vigtig del af matematikken og datalogien. For mange af disse problemer findes der nøjagtige løsninger. Mange gange er de imidlertid meget svære at beregne. Derfor anvendes meget ofte tilnærmelser. Der findes to typer af sådanne tilnærmelser, nemlig Monte-Carlo-algoritmer og Las-Vegas-algoritmer.
Spørgsmål og svar
Spørgsmål: Hvad er grafteori?
Svar: Grafteori er et område af matematikken, der studerer grafer, som er abstrakte repræsentationer af punkter, der er forbundet af linjer.
Spørgsmål: Hvad kaldes punkterne i en graf?
Svar: Punkterne i en graf kaldes normalt for hjørner.
Sp: Hvad repræsenterer linjerne mellem toppene?
Svar: Linjerne mellem toppene repræsenterer relationer eller forbindelser mellem dem.
Spørgsmål: Hvordan kan grafer bruges?
A: Grafer kan bruges til at modellere relationer og finde svar på forskellige problemer.
Sp: Hvilke spørgsmål kan grafer hjælpe med at besvare?
Svar: Grafer kan hjælpe med at besvare spørgsmål i forbindelse med netværksanalyse, optimering og planlægning.
Spørgsmål: Er der forskellige typer grafer?
A: Ja, der findes forskellige typer grafer, f.eks. retningsbestemte og uretningsbestemte grafer, vægtede og uvægtede grafer, komplette og ufuldstændige grafer osv.
Spørgsmål: Findes der software til at arbejde med grafteori?
A: Ja, der findes software til at arbejde med grafteori, f.eks. Gephi og NetworkX.
