AlegsaOnline.com

Firefarvesætningen: Definition, bevis og betydning i matematik

Firefarvesætningen: klar definition, historisk og moderne computerbevis samt betydning i matematik — forstå bevismetoder, eksempler og konsekvenser.

Forfatter: Leandro Alegsa

14-12-2025

Theoremet om de fire farver er et matematisk teorem. Det siger, at på enhver plan flade med regioner (folk tænker på dem som kort) kan regionerne ikke farves med mere end fire farver. To regioner, der har en fælles grænse, må ikke få den samme farve. De kaldes tilstødende (ved siden af hinanden), hvis de deler et segment af grænsen, ikke blot et punkt.

Dette var den første sætning, der blev bevist af en computer, i et bevis ved udtømning. Ved et udtømmende bevis fastslås konklusionen ved at opdele den i tilfælde og bevise hvert enkelt tilfælde separat. Der kan være mange tilfælde. F.eks. var det første bevis for firefarvetheoremet et udtømmende bevis med 1 936 tilfælde. Dette bevis var kontroversielt, fordi de fleste af tilfældene blev kontrolleret af et computerprogram og ikke i hånden. Det korteste kendte bevis for firefarvesætningen har i dag stadig over 600 tilfælde.

Selv om problemet først blev præsenteret som et problem med at farvelægge politiske kort over lande, er kortmagere ikke særlig interesserede i det. Ifølge en artikel af matematikhistorikeren Kenneth May (Wilson 2002, 2) er det sjældent, at kort, der kun anvender fire farver, og de kort, der gør det, kræver normalt kun tre. Bøger om kartografi og kortfremstillingens historie nævner ikke den firefarvede egenskab."

Mange enklere kort kan farvelægges med tre farver. Den fjerde farve er nødvendig for nogle kort, f.eks. et kort, hvor et område er omgivet af et ulige antal andre områder, som berører hinanden i en cyklus. Et sådant eksempel er vist på billedet. Teoremet om fem farver siger, at fem farver er nok til at farve et kort. Det har et kort, elementært bevis og blev bevist i slutningen af det 19. århundrede. (Heawood 1890) At bevise, at fire farver er nok, viste sig at være langt vanskeligere. Der er dukket mange falske beviser og falske modeksempler op siden den første udtalelse om sætningen om de fire farver i 1852.

Formulering i grafteori

Teoremet kan også formuleres i termer af grafteori: et planært kort svarer (via dualgrafen) til en planær graf, og det at farve regioner svarer til at farve noder i den duale graf, så ingen to tilstødende noder har samme farve. Dermed er firefarvesætningen ækvivalent med påstanden: »Enhver planær graf kan vertex-farves med højest fire farver.« Denne formulering gør det muligt at bruge grafteoretiske metoder i beviser og konstruktioner.

Kort oversigt over bevisidéer

Minimalt modeksempel: Man antager, at der findes et modeksempel (et kort, der kræver fem farver) og vælger et med færrest mulige regioner. Ideen er at vise, at et sådant minimalmodeksempel ikke kan eksistere, fordi man altid kan reducere det til et mindre eksempel.
Reducerbare konfigurationer: Man identificerer små lokale mønstre (konfigurationer) i et kort, som ikke kan optræde i et ægte modeksempel, fordi de kan omfarves eller fjernes uden at ødelægge farvbarheden. Disse mønstre kaldes reducerbare.
Uundgåelighedsæt (unavoidable set): Ved hjælp af en såkaldt discharging-metode (udladningsmetode) viser man, at ethvert planært kort må indeholde mindst en af et bestemt, begrænset antal konfigurationer. Hvis alle disse konfigurationer er reducerbare, kan et modeksempel ikke eksistere.
Kempe-kæder: Et centralt værktøj i forsøgene på at reducere farver er Kempe-kæder — kæder af vekselvis farvede regioner, som man kan bytte farver på for at få plads til en ekstra farve. Kempe brugte denne idé i et berømt, men fejlagtigt bevis fra 1879; teknikken er dog stadig vigtig i moderne beviser.

Historik og store milepæle

Første formulering: problemet blev formuleret i 1852 og tiltrak megen opmærksomhed i slutningen af 1800-tallet.
Kempe (1879) fremlagde et bevis, som blev anset for korrekt i næsten et årti, men senere blev en fejl opdaget (Heawood 1890 fandt problemet).
Fem-farver-sætningen blev bevist af Heawood i 1890, hvilket viste, at fem farver altid er tilstrækkelige.
Det første computerassisterede bevis kom i 1976 af Appel og Haken, som reducerede problemet til 1.936 tilfælde, kontrolleret ved hjælp af computerprogrammer. Dette bevis var historisk, men også omdiskuteret pga. den omfattende computerassistance.
Senere forbedringer af Appel–Haken-ideen, især arbejdet af Robertson, Sanders, Seymour og Thomas i 1997, reducerede antallet af nødvendige tilfælde (ofte citeret som 633) og gav et mere strømlinet bevis, men computerassistance var stadig nødvendig.
Formalisering: I det 21. århundrede er dele af beviset blevet formaliseret i bevisassistenter (fx Coq), hvilket øger tilliden til korrektheden af de computer-assisterede dele (Georges Gonthier og samarbejdspartnere).

Betydning og anvendelser

Ud over sin tilsyneladende simple formulering har firefarvesætningen haft stor betydning inden for matematikhistorie, grafteori og beregningsmetode. Den var en af de første store sætninger, hvor computerhjælp blev brugt på afgørende vis, og den udløste debat om, hvad et matematisk bevis kræver. Metoder udviklet i forbindelse med sætningen — især discharging-metoden — bruges også i andre resultater i planær grafteori.

Begrænsninger og praktisk relevans

Som teksten ovenfor nævner, er teorien først og fremmest af teoretisk interesse. I praktiske kartografiske opgaver ender man sjældent med situationer, hvor præcis fire farver er nødvendige; mange naturlige kort kan klare sig med tre farver eller andre layout- og designløsninger. Alligevel forbliver problemet et centralt og klassisk element i matematikundervisning og populærvidenskabelige fremstillinger af matematik.

Relaterede problemer og generaliseringer

Hadwigers formodning: En generalisering til højere dimensioner og kromatiske tal, som bl.a. indeholder den firefarvede form som et særligt tilfælde.
Planære grafer: Mange resultater om farvning og strukturer i planære grafer er inspireret af teknikker brugt i eller udviklet til firefarvesætningen.

Samlet set er firefarvesætningen et godt eksempel på, hvordan et enkelt, letforståeligt spørgsmål kan føre til dybe metoder, langvarige diskussioner og ny udvikling inden for matematik og computervidenskab.

Tre farver er ikke nok til at farvelægge dette kort.

Præcis formulering af problemet

Intuitivt kan sætningen om de fire farver formuleres således: "Når et plan er opdelt i sammenhængende regioner, kaldet et kort, kan regionerne farves med højst fire farver, så ingen af de to regioner, der støder op til hinanden, har den samme farve". For at kunne løse problemet korrekt er det nødvendigt at afklare nogle aspekter: For det første skal alle punkter, der hører til tre eller flere lande, ignoreres. For det andet kan bizarre kort med regioner med begrænset areal og uendelig omkreds kræve mere end fire farver.

Med henblik på teoremet skal hvert "land" være et enkelt sammenhængende område eller sammenhængende. I den virkelige verden er dette ikke tilfældet: Alaska som en del af USA, Nakhchivan som en del af Aserbajdsjan og Kaliningrad som en del af Rusland er ikke sammenhængende. Fordi et lands territorium skal have samme farve, er fire farver måske ikke nok. Se f.eks. på et forenklet kort som det, der er vist til venstre: På dette kort tilhører de to regioner, der er mærket med A, det samme land og skal have samme farve. Dette kort kræver altså fem farver, da de to A-regioner tilsammen støder op til fire andre regioner, som hver især støder op til alle de andre regioner. Hvis A kun havde tre regioner, ville der måske være behov for seks eller flere farver. På denne måde er det muligt at lave kort, der kræver et vilkårligt højt antal farver. En lignende konstruktion gælder også, hvis der anvendes en enkelt farve for alle vandområder, som det er almindeligt på virkelige kort.

En nemmere version af teoremet er baseret på grafteori. Mængden af regioner i et kort kan mere abstrakt fremstilles som en udirigeret graf, der har et toppunkt for hver region og en kant for hvert par regioner, der deler et grænsesegment. Denne graf er planar: den kan tegnes i planen uden krydsninger ved at placere hvert toppunkt på et vilkårligt valgt sted i den region, som det svarer til, og ved at tegne kanterne som kurver, der uden krydsninger fører i hver region fra toppunktets placering til hvert fælles grænsepunkt i regionen. Omvendt kan enhver planar graf dannes ud fra et kort på denne måde. I grafteoretisk terminologi siger firefarveteoremet, at toppene i enhver planar graf kan farves med højst fire farver, således at ingen to tilstødende toppene har samme farve, eller kort sagt, "enhver planar graf er firefarvet" (Thomas 1998, s. 849; Wilson 2002).

Eksempel på et kort over Aserbajdsjan med ikke-sammenhængende regioner

Dette kort kan ikke farvelægges med fire farver

Historie

Den første person, der navngav problemet, var Francis Guthrie i 1852. Han var jurastuderende i England på det tidspunkt. Han fandt ud af, at han havde brug for mindst fire farver for at farvelægge et kort over de engelske amter. Augustus de Morgan diskuterede problemet første gang i et brev, som han skrev til Rowan Hamliton i august 1852. I brevet spørger de Morgan, om fire farver virkelig er nok til at farvelægge et kort, således at lande, der ligger ved siden af hinanden, får forskellige farver.

Den engelske matematiker Arthur Cayley præsenterede problemet for det matematiske selskab i London i 1878. Inden for et år fandt Alfred Kempe noget, der lignede et bevis for problemet. Elleve år senere, i 1890, viste Percy Heawood, at Alfreds bevis var forkert. Peter Guthrie Tait fremlagde endnu et forsøg på et bevis i 1880. Det tog elleve år at vise, at Tait's bevis heller ikke virkede. I 1891 kunne Julius Petersen vise dette. Da han falsificerede Cayleys bevis, viste Kempe også et bevis for et problem, som han kaldte Five color theorem. Sætningen siger, at ethvert sådant kort kan farvelægges med højst fem farver. Der er to begrænsninger: For det første er ethvert land sammenhængende, der er ingen eksklaver. Den anden begrænsning er, at landene skal have en fælles grænse; hvis de kun berører hinanden i et punkt, kan de farves med den samme farve. Selv om Kempe's bevis var forkert, brugte han nogle af de idéer, som senere ville gøre det muligt at lave et korrekt bevis.

I 1960'erne og 1970'erne udviklede Heinrich Heesch en første skitse til et computerbevis. Kenneth Appel og Wolfgang Haken forbedrede denne skitse i 1976 (Robertson et al. 1996). De var i stand til at reducere antallet af tilfælde, der skulle testes, til 1936; der blev lavet en senere version, som kun var afhængig af at teste 1476 tilfælde. Hvert tilfælde skulle testes af en computer (Appel & Haken 1977) harv fejl: flere mål (2×): CITEREFAppelHaken1977 (help).

I 1996 forbedrede Neil Robertson, Daniel Sanders, Paul Seymour og Robin Thomas metoden og reducerede antallet af tilfælde, der skulle testes, til 663. Igen skulle hvert enkelt tilfælde testes ved hjælp af en computer.

I 2005 udviklede Georges Gonthier og Benjamin Werner et formelt bevis. Dette var en forbedring, fordi det for første gang gjorde det muligt at anvende software til teoremafprøvning. Den anvendte software hedder Coq.

Firefarveteoremet er det første store matematiske problem, der blev løst ved hjælp af en computer. Fordi beviset ikke kan udføres af et menneske, anerkendte nogle matematikere det ikke som korrekt. For at verificere beviset er det nødvendigt at stole på en korrekt fungerende software og hardware for at validere beviset. Fordi beviset blev udført af en computer, er det heller ikke særlig elegant.

Forsøg, der viste sig at være forkerte

Firefarvesætningen har været berygtet for at have tiltrukket et stort antal falske beviser og modbeviser i sin lange historie. I første omgang nægtede New York Times at rapportere om Appel-Haken-beviset. Avisen gjorde dette af politiske årsager; den frygtede, at beviset ville blive vist som falsk ligesom de tidligere beviser (Wilson 2002, s. 209). Nogle beviser tog lang tid, før de kunne forfalskes: For Kempe's og Tait's beviser tog det over et årti at falsificere dem.

De enkleste modeksempler forsøger generelt at skabe et område, som berører alle de andre. Dette tvinger de resterende regioner til kun at blive farvet med tre farver. Da firefarveteoremet er sandt, er dette altid muligt; men fordi den person, der tegner kortet, er fokuseret på den ene store region, bemærker han ikke, at de resterende regioner faktisk kan farves med tre farver.

Dette trick kan generaliseres: Hvis farverne på nogle områder i et kort er valgt på forhånd, bliver det umuligt at farve de resterende områder på en sådan måde, at der i alt kun anvendes fire farver. En person, der verificerer modeksemplet, tænker måske ikke på, at det kan være nødvendigt at ændre farven på disse regioner. Dette vil få modeksemplet til at se gyldigt ud, selv om det ikke er det.

Måske er en af de virkninger, der ligger til grund for denne almindelige misforståelse, at farvebegrænsningen ikke er transitiv: en region skal kun have en anden farve end de regioner, den berører direkte, og ikke regioner, der berører regioner, som den berører. Hvis dette var begrænsningen, ville plane grafer kræve et vilkårligt stort antal farver.

Andre falske beviser overtræder teoremets forudsætninger på uventede måder, f.eks. ved at bruge et område, der har flere adskilte dele, eller ved ikke at tillade, at områder af samme farve berører hinanden i et punkt.

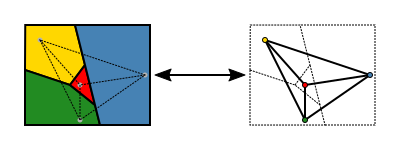
Kortet (til venstre) er blevet farvelagt med fem farver, og det er nødvendigt at ændre mindst fire af de ti regioner for at opnå en farvelægning med kun fire farver (til højre).

Farvelægning af politiske kort

I det virkelige liv har mange lande eksklaver eller kolonier. Da de hører til landet, skal de farves med samme farve som moderlandet. Det betyder, at der normalt er brug for mere end fire farver til at farvelægge et sådant kort. Når matematikere taler om den graf, der er forbundet med problemet, siger de, at den ikke er planar. Selv om det er let at kontrollere, om en graf er planar, er det meget vanskeligt at finde det mindste antal farver, der er nødvendige for at farvelægge den. Det er NP-komplet, hvilket er et af de vanskeligste problemer, der findes. Det mindste antal farver, der er nødvendige for at farvelægge en graf, kaldes dens kromatiske tal. Mange af de problemer, der opstår, når man forsøger at løse sætningen om de fire farver, er relateret til diskret matematik. Derfor anvendes der ofte metoder fra algebraisk topologi.

Udvidelse til "ikke-flade" kort

Sætningen om de fire farver kræver, at "kortet" er på en flad overflade, det, som matematikere kalder et plan. I 1890 skabte Percy John Heawood det, der i dag kaldes Heawood-konjekturen: Den stiller det samme spørgsmål som firefarvetheoremet, men for ethvert topologisk objekt. Som et eksempel kan en torus højst farves med syv farver. Heawoods formodning giver en formel, der virker for alle sådanne objekter, undtagen Klein-flasken.

Spørgsmål og svar

Spørgsmål: Hvad er firefarveteoremet?

A: Firefarveteoremet er et matematisk teorem, der siger, at i enhver plan overflade med regioner kan regionerne ikke farves med mere end fire farver. Tilstødende regioner må ikke få samme farve.

Spørgsmål: Hvordan blev det første bevis for firefarvesætningen opstillet?

Svar: Det første bevis for firefarvet sætning var et bevis ved udtømning med 1 936 tilfælde. Det betyder, at det blev fastslået ved at opdele det i tilfælde og bevise hvert enkelt tilfælde for sig.

Spørgsmål: Er kortmagere interesseret i dette problem?

Svar: Nej, kortmagere er ikke særlig interesserede i dette problem, da kort, der kun anvender fire farver, er sjældne og normalt kun kræver tre farver. Bøger om kartografi og kortfremstillingens historie nævner ikke den firefarvede egenskab.

Spørgsmål: Hvad er teoremet om de fem farver?

A: Femfarveteoremet siger, at fem farver er nok til at farvelægge et kort, og det har et kort, elementært bevis, som blev bevist i slutningen af det 19. århundrede.

Spørgsmål: Hvor vanskeligt var det at bevise, at der kun var brug for fire farver til farvelægning af kort?

Svar: Det viste sig at være meget vanskeligere end forventet at bevise, at der kun var behov for fire farver til farvelægning af kort, da der er fremkommet mange falske beviser og falske modeksempler siden den første påstand i 1852.

Spørgsmål: Findes der et eksempel på et kort, hvor 5 eller flere farver ville være nødvendige for at farvelægge alle regioner korrekt?

A: Ja, et sådant eksempel er, når et område er omgivet af et ulige antal andre områder, som berører hinanden i en cyklus - i dette tilfælde kan det være nødvendigt med 5 eller flere farver for at få alle områderne farvelagt korrekt.