AlegsaOnline.com

Algebra: Definition, ligninger, funktioner og grundlæggende anvendelser

Lær algebra: definition, ligninger, funktioner og praktiske anvendelser — enkel forklaring, eksempler og anvendelser i fysik, ingeniørarbejde, programmering og hverdagsproblemer.

Forfatter: Leandro Alegsa Oprettelsesdato: 7. december 2021 Seneste opdatering: 6. oktober 2025

simple.wikipedia.org · CC BY-SA 3.0

Algebra (fra arabisk: الجبر, translittereret "al-jabr", der betyder "genforening af brudstykker") er en gren af matematikken, som arbejder med symboler og regler for at manipulere disse symboler. I algebra bruges variabler (typisk bogstaver som x og y) til at repræsentere tal eller mængder, hvis præcise værdi er ukendt eller kan variere. Ved hjælp af algebra kan man beskrive mønstre, opstille formler, løse ligninger og analysere sammenhænge mellem størrelser i både teoretiske og praktiske problemstillinger.

Grundlæggende begreber

En af de mest grundlæggende idéer i algebra er en ligning, hvor et lighedstegn (=) fortæller, at to udtryk har samme værdi. For eksempel:

En meget simpel ligning, der anvender en variabel, er: 2 + 3 = x {\displaystyle 2+3=x} $2+3=x$ . I dette eksempel er x = 5 {\displaystyle x=5} $x=5$ , eller man kan også sige, at "x {\displaystyle x} er lig med fem". Dette kaldes at løse for x {\displaystyle x}.

Ud over ligninger arbejder algebra også med uligheder, som udtrykker relationer som mindre end (<) og større end (>). En anden central idé er en funktion, som beskriver en sammenhæng hvor hvert input har ét output. Funktionen er særligt nyttig, når man vil lave grafer og visualisere, hvordan én størrelse afhænger af en anden.

Grundlæggende regler og operationer

Algebra bygger på de samme regler for tal og regneoperationer som almindelig aritmetik. De mest almindelige operationer er:

addition (at addere)
subtraktion (at trække fra)
multiplikation (at gange)
division (at dividere)

Mere avancerede operationer inkluderer eksponenter — for eksempel kvadrater og kvadratrødder. Eksponenter angiver gentagen multiplikation, f.eks. er 2 gange 2 det samme som 2² (to i anden).

Ligninger og metoder til løsning

Algebra opstod i stor udstrækning for at kunne løse ligninger og uligheder. To af de mest centrale typer ligninger i grundlæggende algebra er:

Lineære ligninger — disse beskriver rette linjer og har formen y = m x + b {\displaystyle y=mx+b} $y=mx+b$ (eller y = m x + c {\displaystyle y=mx+c} $y=mx+c$ ), hvor m er hældningen og b eller c er konstanten (y-aksens skæringspunkt).
Kvadratiske ligninger — disse indeholder variabler, som er kvadreret (ganget med sig selv). Eksempelvis kan udtryk som 2⋅2 eller 3⋅3 bruges til at forstå kvadrering, og et algebraisk eksempel er x⋅x. Kvadratiske ligninger har typisk formen ax² + bx + c = 0 og kan løses ved faktorisering, ved at bruge kvadratsætninger eller med den klassiske løsningsformel (discriminantmetoden).

Typiske metoder til at løse ligninger i algebra omfatter:

Omskrivning af ligningen så variablen isoleres (for lineære ligninger).
Faktorisering (find fælles faktorer eller faktorisér et polynomium).
Brug af kvadratsætninger og den kvadratiske formel for andengradsligninger.
Substitution eller eliminering ved systemer af ligninger.

Funktioner, grafer og sammenhænge

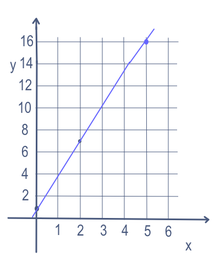
En funktion knytter hvert input (ofte kaldet x) til præcis ét output (ofte kaldet y). Funktioner kan være lineære, kvadratiske eller langt mere komplicerede. Når man tegner funktionen som en graf i et koordinatsystem, bliver forholdet mellem input og output synligt — f.eks. en lige linje for lineære funktioner eller en parabel for kvadratiske funktioner.

Vigtige begreber i arbejdet med funktioner er blandt andet:

Domæne (de tilladte inputværdier)
Værdimængde eller rækkevidde (de mulige outputværdier)
Nulsteder (hvor funktionen er lig med nul)
Hældning og skæringspunkter (for lineære funktioner)

Anvendelser i virkeligheden

Algebra er et praktisk redskab, fordi de regler, man bruger i algebra, ofte afspejler forhold i den fysiske verden. Man kan bruge algebra til at modellere og løse problemer inden for mange fagområder:

Fysik — beregning af bevægelse, kræfter, energi mv.
Ingeniørvidenskab — design, analyse og beregninger.
Computerprogrammering — algoritmer og beregninger bygger ofte på algebraiske idéer.
Praktiske fag som landmåling, byggeri og erhvervsliv, især regnskab, hvor tal og formler anvendes dagligt.

Udvidelser og videre emner

Når man går videre i algebra, møder man begreber som polynomier, rationelle funktioner, eksponentielle og logaritmiske funktioner, matricer og lineær algebra samt abstrakte strukturer som grupper, ringe og kroppe. Disse udvidelser bruges både i ren matematik og i mange anvendelser inden for videnskab og teknik.

Kort historik

Navnet algebra stammer fra det arabiske værk, hvor ordet al-jabr optræder. Historisk har algebra udviklet sig fra konkrete regneregler og løsning af bestemte ligningstyper til et abstrakt sprog, der gør det muligt at formulere og bevise generelle resultater. I dag er algebra både et praktisk værktøj og et teoretisk fagområde med mange underdiscipliner.

Ved at lære algebra opnår man ikke kun evnen til at løse ligninger, men også et systematisk værktøjssæt til at beskrive og analysere relationer mellem størrelser — noget der er nyttigt i både skole, studie og arbejde.

Historie

De tidlige former for algebra blev udviklet af babylonierne og de græske geometriker som Hero af Alexandria. Ordet "algebra" er imidlertid en latinsk form af det arabiske ord Al-Jabr ("støbning") og stammer fra en matematikbog Al-Maqala fi Hisab-al Jabr wa-al-Muqabilah ("Essay on the Computation of Casting and Equation"), der blev skrevet i det 9. århundrede af en persisk matematiker, Muhammad ibn Mūsā al-Khwārizmī, som var muslim og født i Khwarizm i Usbekistan. Han blomstrede under Al-Ma'moun i Baghdad i Irak i årene 813-833 e.Kr. og døde omkring 840 e.Kr. Bogen blev bragt til Europa og oversat til latin i det 12. århundrede. Bogen fik derefter navnet "Algebra". (Endelsen på matematikerens navn, al-Khwarizmi, blev ændret til et ord, der var lettere at sige på latin, og blev det engelske ord algorithm).

Eksempler

Her er et simpelt eksempel på en algebraopgave:

Sue har 12 slik, og Ann har 24 slik. De beslutter sig for at dele, så de har det samme antal slik. Hvor mange bolsjer får de hver især?

Dette er de trin, du kan bruge til at løse problemet:

For at få det samme antal slik skal Ann give nogle af dem til Sue for at få det samme antal. Lad x {\displaystyle x} repræsentere antallet af slik, som Ann giver til Sue.
Sues slik plus x {\displaystyle x} , må være det samme som Anns slik minus x {\displaystyle x} . Dette skrives som: 12 + x = 24 - x {\displaystyle 12+x=24-x} $12+x=24-x$
Træk 12 fra begge sider af ligningen. Dette giver: x = 12 - x {\displaystyle x=12-x} $x=12-x$ . (Det, der sker på den ene side af lighedstegnet, skal også ske på den anden side, for at ligningen stadig er sand. Så i dette tilfælde, da 12 blev trukket fra begge sider, var der et mellemtrin på 12 + x - 12 = 24 - x - 12 {\displaystyle 12+x-12=24-x-12} $12+x-12=24-x-12$ . Når en person er blevet fortrolig med dette, skrives det midterste trin ikke ned).
Tilføj x {\displaystyle x} til begge sider af ligningen. Dette giver: 2 x = 12 {\displaystyle 2x=12} $2x=12$
Divider begge sider af ligningen med 2. Det giver x = 6 {\displaystyle x=6} $x=6$ . Svaret er seks. Det betyder, at hvis Ann giver Sue 6 slik, vil de have det samme antal slik.
For at kontrollere dette, skal du sætte 6 tilbage i den oprindelige ligning, hvor x {\displaystyle x} var: 12 + 6 = 24 - 6 {\displaystyle 12+6=24-6} $12+6=24-6$
Dette giver 18 = 18 {\displaystyle 18=18} $18=18$ , hvilket er sandt. De har nu hver 18 slik.

Med lidt øvelse kan algebra bruges, når man står over for et problem, der er for svært at løse på anden vis. Problemer som f.eks. at bygge en motorvej, designe en mobiltelefon eller finde en kur mod en sygdom kræver alle algebra.

Skrivning af algebra

Som i de fleste dele af matematikken skrives det at lægge y {\displaystyle y} til z {\displaystyle z} $z$ (eller y {\displaystyle y} plus z {\displaystyle z} $z$ ) som y + z {\displaystyle y+z} $y+z$ ;

subtraktion af z {\displaystyle z} $z$ fra y {\displaystyle y} (eller y {\displaystyle y} minus z {\displaystyle z} $z$ ) skrives som y - z {\displaystyle y-z} $y-z$ ;

og divideret y {\displaystyle y} med z {\displaystyle z} $z$ (eller y {\displaystyle y} over z {\displaystyle z} $z$ ) skrives som y / z {\displaystyle y/z} $y/z$ eller y z {\displaystyle y \over z} ${y \over z}$ .

I algebra kan multiplikation af y {\displaystyle y} med z {\displaystyle z} $z$ (eller y {\displaystyle y} gange z {\displaystyle z} $z$ ) skrives på 3 forskellige måder: y ⋅ z {\displaystyle y\cdot z} $y\cdot z$ , y ( z ) {\displaystyle y(z)} $y(z)$ eller blot y z {\displaystyle yz} $yz$ . Alle disse betegnelser betyder det samme: y {\displaystyle y} gange z {\displaystyle z} $z$ . Symbolet " × {\displaystyle \times } $\times$ ", der bruges i aritmetik, bruges ikke i algebra, fordi det ligner for meget bogstavet x {\displaystyle x} , der ofte bruges som en variabel.

Når vi multiplicerer et tal og en variabel i algebra, kan vi blot skrive tallet foran bogstavet: 5 ⋅ y ⟺ 5 y {\displaystyle 5\cdot y\iff 5y} $5\cdot y\iff 5y$ . Når tallet er 1, skrives det ikke, fordi 1 gange et tal er dette tal ( 1 ⋅ y = y {\displaystyle 1\cdot y=y} $1\cdot y=y$ ), og det er derfor ikke nødvendigt. Og når det er 0, kan vi helt fjerne termerne, fordi 0 gange et vilkårligt tal er nul ( 0 ⋅ y = 0 {\displaystyle 0\cdot y=0} ). $0\cdot y=0$

Som en sidebemærkning skal du ikke bruge bogstaverne x {\displaystyle x} eller y {\displaystyle y} i algebra. Variabler er blot symboler, der betyder et ukendt tal eller en ukendt værdi, så du kan bruge et hvilket som helst bogstav som variabel (undtagen e {\displaystyle e} $e$ (Eulers tal) og i {\displaystyle i} $i$ (imaginær enhed), fordi det er matematiske konstanter). x {\displaystyle x} og y {\displaystyle y} er dog de mest almindelige.

Funktioner og grafer

En vigtig del af algebra er studiet af funktioner, da de ofte optræder i ligninger, som vi forsøger at løse. En funktion er som en maskine, man kan sætte et tal (eller flere tal) ind og få et bestemt tal (eller flere tal) ud. Når man bruger funktioner, kan grafer være et effektivt redskab til at hjælpe os med at studere ligningernes løsninger.

En graf er et billede, der viser alle de værdier af de variabler, der gør ligningen eller uligheden sand. Det er normalt let at lave, når der kun er en eller to variabler. Grafen er ofte en linje, og hvis linjen ikke bøjer eller går lige op og ned, kan den beskrives med grundformlen y = m x + b {\displaystyle y=mx+b} $y=mx+b$ . Variablen b {\displaystyle b} $b$ er grafens y-intercept (hvor linjen krydser den lodrette akse), og m {\displaystyle m} er linjens hældning eller stejlhed. Denne formel gælder for koordinaterne i en graf, hvor hvert punkt på linjen skrives ( x {\displaystyle x} , y {\displaystyle y} ).

I nogle matematiske problemer, som f.eks. ligningen for en linje, kan der være mere end én variabel (i dette tilfælde x {\displaystyle x} og y {\displaystyle y} ). For at finde punkterne på linjen ændres den ene variabel. Den variabel, der ændres, kaldes den "uafhængige" variabel. Derefter regnes der på det for at lave et tal. Det tal, der er lavet, kaldes den "afhængige" variabel. Oftest skrives den uafhængige variabel som x {\displaystyle x} og den afhængige variabel skrives som y {\displaystyle y} , f.eks. i y = 3 x + 1 {\displaystyle y=3x+1} $y=3x+1$ . Dette sættes ofte på en graf ved hjælp af en x-akse {\displaystyle x} (går til venstre og højre) og en y-akse {\displaystyle y} (går op og ned). Det kan også skrives i funktionsform: f ( x ) = 3 x + 1 {\displaystyle f(x)=3x+1} $f(x)=3x+1$ . Så i dette eksempel kan vi sætte 5 ind for x {\displaystyle x} og få y = 16 {\displaystyle y=16} $y=16$ . Ved at indsætte 2 for x {\displaystyle x} ville vi få y = 7 {\displaystyle y=7} $y=7$ . Og 0 for x {\displaystyle x} ville give y = 1 {\displaystyle y=1} $y=1$ . Der vil altså være en linje, der går gennem punkterne (5,16), (2,7) og (0,1), som det ses på grafen til højre.

Hvis x {\displaystyle x} har en potens på 1, er det en ret linje. Hvis den er kvadreret eller en anden potens, er den kurvet. Hvis der anvendes en ulighed ( < < {\displaystyle <} $<$ eller > {\displaystyle >} $>$ ), er normalt en del af grafen skraveret, enten over eller under linjen.

Regler

I algebra er der nogle få regler, som kan bruges til at forstå ligninger bedre. Disse kaldes algebrareglerne. Selv om disse regler kan virke meningsløse eller indlysende, er det klogt at forstå, at disse egenskaber ikke gælder i alle grene af matematikken. Derfor vil det være nyttigt at vide, hvordan disse aksiomatiske regler er erklæret, før man tager dem for givet. Før vi går videre til reglerne, skal du reflektere over to definitioner, der vil blive givet.

Modsat: Det modsatte af en {\displaystyle a} er - en {\displaystyle -a} .
Reciprok: Reciprokken af en {\displaystyle a} er 1 a {\displaystyle {\frac {\frac {1}{a}}}} ${\frac {1}{a}}$ .

Kommutativ egenskab ved addition

"Kommutativ" betyder, at en funktion har det samme resultat, hvis tallene byttes om på hinanden. Med andre ord betyder rækkefølgen af termerne i en ligning ikke noget. Når to termer (addender) adderes, gælder den "kommutative egenskab ved addition". I algebraiske termer giver dette a + b = b + a {\displaystyle a+b=b+a} a+b=b+a .

Bemærk, at dette ikke gælder for subtraktion (dvs. a - b ≠ b - a {\displaystyle a-b\neq b-a} $a-b\neq b-a$ undtagen hvis a = b {\displaystyle a=b} ). $a=b$

Kommutativ egenskab ved multiplikation

Når to termer (faktorer) multipliceres, gælder den kommutative egenskab ved multiplikation. I algebraiske termer giver det a ⋅ b = b ⋅ a {\displaystyle a\cdot b=b\cdot a} $a\cdot b=b\cdot a$ .

Bemærk, at dette ikke gælder for division (dvs. a b ≠ b a {\displaystyle {\frac {\frac {a}{b}}}\neq {\frac {b}{a}}}} ${\frac {a}{b}}\neq {\frac {b}{a}}$ , når a ≠ 0 {\displaystyle a\neq 0} $a\neq 0$ og b ≠ 0 {\displaystyle b\neq 0} $b\neq 0$ , undtagen hvis a = b {\displaystyle a=b} ). $a=b$

Associerende egenskab ved addition

"Associativ" henviser til gruppering af tal. Den associative egenskab ved addition indebærer, at når man adderer tre eller flere termer, er det ligegyldigt, hvordan disse termer er grupperet. Algebraisk set giver dette a + ( b + c ) = ( a + b ) + c {\displaystyle a+(b+c)=(a+b)+c} . Bemærk, at dette ikke gælder for subtraktion, f.eks. 1 - ( 2 - 3 ) ≠ ( 1 - 2 ) - 3 {\displaystyle 1-(2-3)\neq (1-2)-3} $1-(2-3)\neq (1-2)-3$ (se distributiv egenskab).

Associerende egenskab ved multiplikation

Den associative egenskab ved multiplikation indebærer, at når man multiplicerer tre eller flere termer, er det ligegyldigt, hvordan disse termer er grupperet. Algebraisk set giver dette a ( b c ) = ( a b ) c {\displaystyle a(bc)=(ab)c} $a(bc)=(ab)c$ . Bemærk, at dette ikke gælder for division, f.eks. 1 / ( 2 / 4 ) ≠ ( 1 / 2 ) / 4 {\displaystyle 1/(2/4)\neq (1/2)/4} $1/(2/4)\neq (1/2)/4$ .

Distributiv egenskab

Den distributive egenskab siger, at multiplikationen af et udtryk med et andet udtryk kan distribueres. For eksempel: a ( b + c ) = a b + a c {\displaystyle a(b+c)=ab+ac} $a(b+c)=ab+ac$ . (Dette må ikke forveksles med de associative egenskaber! For eksempel: a ( b + c ) ≠ ( a b ) + c {\displaystyle a(b+c)\neq (ab)+c} $a(b+c)\neq (ab)+c$ .)

Additiv identitet

"Identitet" henviser til den egenskab ved et tal, at det er lig med sig selv. Med andre ord findes der en operation af to tal, så det er lig med summen af variablen. Den additive identitetsegenskab fastslår, at ethvert tal plus 0 er dette tal: a + 0 = a {\displaystyle a+0=a} a+0=a . Dette gælder også for subtraktion: a - 0 = a {\displaystyle a-0=a} a-0=a .

Multiplikativ identitet

Den multiplikative identitetsegenskab siger, at ethvert tal gange 1 er dette tal: a ⋅ 1 = a {\displaystyle a\cdot 1=a} $a\cdot 1=a$ . Dette gælder også for division: a 1 = a {\displaystyle {\frac {a}{1}}}=a} ${\frac {a}{1}}=a$ .

Additiv omvendt egenskab

Den additive inverse egenskab er lidt som det modsatte af den additive identitet. Når vi adderer et tal og dets modsætning, er resultatet 0. Algebraisk set lyder det således: a + - a = 0 {\displaystyle a+-a=0} $a+-a=0$ , hvilket er det samme som a - a = 0 {\displaystyle a-a=0} $a-a=0$ . F.eks. er den additive inverse (eller modsatte) af 1 -1.

Multiplikativ omvendt egenskab

Den multiplikative inverse egenskab betyder, at når vi multiplicerer et tal med dets inverse, er resultatet 1. Algebraisk set siger den følgende: a ⋅ $a\cdot {\frac {1}{a}}=1$ , hvilket er det samme som a a a = 1 {\displaystyle {\frac {a}{a}}}=1} ${\frac {a}{a}}=1$ . F.eks. er den multiplikative inverse (eller bare inverse) af 2 1/2. For at få inversen af en brøk skal man bytte om på tælleren og nævneren: Inversen af 2 3 {\displaystyle {\frac {\frac {2}{3}}}}} ${\frac {2}{3}}$ er 3 2 {\displaystyle {\frac {\frac {3}{2}}}} ${\frac {3}{2}}$ .

Avanceret algebra

Ud over "elementær algebra" eller grundlæggende algebra findes der avancerede former for algebra, som undervises på universiteter og højere læreanstalter, såsom abstrakt algebra, lineær algebra og universel algebra. Dette omfatter, hvordan man bruger en matrix til at løse mange lineære ligninger på én gang. Abstrakt algebra er studiet af ting, der findes i ligninger, og som går ud over tal til det mere abstrakte med grupper af tal.

Mange matematikopgaver handler om fysik og teknik. I mange af disse fysikproblemer er tid en variabel. Det bogstav, der anvendes for tid, er t {\displaystyle t} $t$ . Ved at bruge de grundlæggende ideer i algebra kan man reducere et matematisk problem til sin enkleste form, hvilket gør det lettere at løse vanskelige problemer. Energi er e {\displaystyle e} $e$ , kraft er f {\displaystyle f} , masse er m {\displaystyle m} , acceleration er a {\displaystyle a} og lysets hastighed er undertiden c {\displaystyle c} $c$ . Dette bruges i nogle berømte ligninger, som f = m a {\displaystyle f=ma} $f=ma$ og e = m c 2 {\displaystyle e=mc^{2}}} $e=mc^{2}$ (selv om der var behov for mere kompleks matematik end algebra for at finde frem til den sidste ligning).

Relaterede sider

Liste over matematiske emner
Arbejdsgangsorden
Parabel
Computer-algebra-system

Spørgsmål og svar

Spørgsmål: Hvad er algebra?

A: Algebra er en del af matematikken, der bruger variabler til at repræsentere en værdi, der endnu ikke er kendt.

Spørgsmål: Hvad betyder et lighedstegn i algebra?

A: Et lighedstegn (=) betegner en ligning i algebra.

Sp: Hvad er en funktion i algebra?

A: En funktion i algebra er en særlig type ligning, der altid omdanner et input til et output.

Spørgsmål: Hvordan kan algebra bruges til at løse virkelige problemer?

A: Algebra kan bruges til at løse virkelige problemer, fordi algebraens regler fungerer i det virkelige liv, og tal kan bruges til at repræsentere værdierne af virkelige ting. Fysik, ingeniørvidenskab og computerprogrammering er områder, hvor algebra anvendes hele tiden. Det er også nyttigt at have kendskab til det inden for landmåling, byggeri og erhvervsliv, især regnskab.

Spørgsmål: Hvilke matematiske operationer anvendes på tal i algebra?

A: I algebra bruger man talreglerne og matematiske operationer som f.eks. addition, subtraktion, multiplikation og division af tal. Mere avancerede operationer involverer eksponenter, begyndende med kvadrater og kvadratrødder.

Spørgsmål: Hvad er eksempler på ligninger, der bruges i algebra?

A: Eksempler på ligninger, der anvendes i algebra, omfatter lineære ligninger (ligningen for en lige linje) og kvadratiske ligninger, som har variabler, der er kvadreret (ganget med sig selv).