Trigonometri: Definition, vinkler, trekanter og funktioner (sin, cos, tan)

Få en klar introduktion til trigonometri: definition, vinkler, trekanter og trigonometriske funktioner (sin, cos, tan) med konkrete forklaringer og eksempler.

Trigonometri (af græsk trigonon = tre vinkler og metron = mål) er en del af den elementære matematik, der beskæftiger sig med vinkler, trekanter og trigonometriske funktioner som sinus (forkortet sin), cosinus (forkortet cos) og tangens (forkortet tan). Den har en tæt forbindelse til geometri og anvendes bredt inden for blandt andet navigation, fysik, ingeniørarbejde, astronomi og signalbehandling.

Vinkler og måleenheder

Vinkler måles oftest i grader (°) eller i radianer (rad). Et helt omløb svarer til 360° = 2π rad, så omregningen mellem grader og radianer er

• 1° = π/180 rad
• 1 rad = 180/π °

Vinkler kan være positive eller negative afhængigt af rotationsretningen, og i analytisk trigonometri placeres vinkler ofte i standardposition med hjørnet i origo og spidsen på enhedscirklen.

Retvinklet trekant og de grundlæggende funktioner

I en retvinklet trekant defineres de trigonometriske funktioner for en af de skarpe vinkler α således:

• sin(α) = (modstående katete) / (hypotenusen)
• cos(α) = (hosliggende katete) / (hypotenusen)
• tan(α) = (modstående katete) / (hosliggende katete) = sin(α)/cos(α)

Et almindeligt huskemiddel er SOHCAHTOA (Sine = Opposite/Hypotenuse, Cosine = Adjacent/Hypotenuse, Tangent = Opposite/Adjacent).

Enhedscirklen og udvidelse til alle vinkler

Trigonometriske funktioner kan defineres for alle reelle vinkler ved hjælp af enhedscirklen (cirkel med radius 1). For en vinkel θ svarer punktet på cirklen (cos θ, sin θ). Denne definition giver funktionerne periodiske egenskaber og beskriver fortegnene i de fire kvadranter.

Værdier for særlige vinkler

• 0°: sin = 0, cos = 1, tan = 0
• 30°: sin = 1/2, cos = √3/2, tan = 1/√3
• 45°: sin = √2/2, cos = √2/2, tan = 1
• 60°: sin = √3/2, cos = 1/2, tan = √3
• 90°: sin = 1, cos = 0, tan = udefineret

Vigtige identiteter

• Pythagoras-identitet: sin²x + cos²x = 1
• Even/odd: cos(−x) = cos x, sin(−x) = −sin x, tan(−x) = −tan x
• Periodiciteter: sin(x + 2π) = sin x, cos(x + 2π) = cos x, tan(x + π) = tan x
• Additionsformler:
  • sin(α + β) = sin α cos β + cos α sin β
  • cos(α + β) = cos α cos β − sin α sin β
  • tan(α + β) = (tan α + tan β) / (1 − tan α tan β)
• Dobbeltvinkelformler: sin 2x = 2 sin x cos x, cos 2x = cos²x − sin²x = 2 cos²x − 1 = 1 − 2 sin²x

Inverse funktioner og beregning

De inverse trigonometriske funktioner er arcsin, arccos og arctan (ofte skrevet som sin⁻¹, cos⁻¹, tan⁻¹). De anvendes til at bestemme vinkler ud fra kendte forhold mellem sider. For numeriske beregninger bruges lommeregnere eller computersoftware, der typisk kan arbejde i grader eller radianer efter valg.

Trigonometrisk regning i ikke-retvinklede trekanter

For vilkårlige trekanter bruges to centrale sætninger:

• Sine-loven: a / sin A = b / sin B = c / sin C, hvor a, b, c er sidelængder og A, B, C de modstående vinkler.
• Cosinus-loven: c² = a² + b² − 2ab cos C, som generaliserer Pythagoras' sætning og bruges til at finde en side eller en vinkel i en vilkårlig trekant.

Relation til calculus

De trigonometriske funktioner har velkendte differential- og integralregneregler, f.eks.:

• d/dx [sin x] = cos x
• d/dx [cos x] = −sin x
• ∫ sin x dx = −cos x + C, ∫ cos x dx = sin x + C

Anvendelser

Trigonometri anvendes i mange praktiske sammenhænge, bl.a.:

• Navigations- og positionsbestemmelse (GPS, sejlads, luftfart)
• Bygningskonstruktion og ingeniørprojekter
• Bølger og oscillationer i fysik (lyd, lys, elektromagnetiske bølger)
• Signalbehandling og Fourier-analyse
• Astronomi til bestemmelse af afstande og vinkler mellem himmellegemer

Kort historisk note

Trigonometri har rødder i oldtidens civilisationer og blev formelt udviklet af græske og indiske astronomer. Navnene og begreberne stammer fra græsk, som nævnt i åbningen, og udviklingen af trigonometriske tabeller var central for tidlig astronomi.

Denne gennemgang dækker de grundlæggende definitioner, væsentlige identiteter og praktiske anvendelser. For videre studier anbefales arbejdet med enhedscirklen, graftegning og anvendelse af addition- og dobbeltvinkelformler i opgaveløsning.

Oversigt og definitioner

Trigonometri bruger et stort antal specifikke ord til at beskrive dele af en trekant. Nogle af definitionerne i trigonometri er:

• Retvinklet trekant - En retvinklet trekant er en trekant, hvis vinkel er lig med 90 grader. (En trekant kan ikke have mere end én retvinklet vinkel) De trigonometriske standardforhold kan kun anvendes på retvinklede trekanter.
• Hypotenuse - Hypotenusen i en trekant er den længste side og den side, der er modsat den rette vinkel. For eksempel er hypotenusen i trekanten til højre siden c.
• Modsat side af en vinkel - Den modsatte side af en vinkel er den side, der ikke skærer vinkelens toppunkt. F.eks. er side a den modsatte side af vinkel A i trekanten til højre.
• Tilstødende side til en vinkel - Den tilstødende side til en vinkel er den side, der skærer vinkelens toppunkt, men som ikke er hypotenusen. F.eks. er side b naboside til vinkel A i trekanten til højre.

 
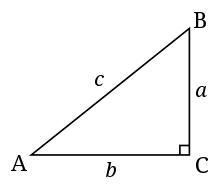
En almindelig retvinklet trekant. C er den rette vinkel i dette billede  

Søg efter bogstav