Statistik – definition, metoder og anvendelser i videnskab og samfund
Statistik: lær definition, metoder og praktiske anvendelser i videnskab, medicin, økonomi og samfund — fra dataindsamling og beskrivelse til inferens og beslutningsstøtte.
Statistik er en gren af den anvendte matematik, der beskæftiger sig med indsamling, organisering, analyse, læsning og præsentation af data. Deskriptiv statistik opsummerer data. I inferentialstatistik foretages forudsigelser. Statistik er en hjælp til undersøgelse af mange andre områder, f.eks. videnskab, medicin, økonomi, psykologi, politik og markedsføring. En person, der arbejder med statistik, kaldes en statistiker. Ud over at være navnet på et forskningsområde kan ordet "statistik" også betyde tal, der bruges til at beskrive data eller sammenhænge.
Hvad er statistik — kort forklaring
Statistik omfatter metoder og værktøjer til at gøre rå data forståelige og anvendelige. Det indebærer at vælge, indsamle og organisere relevante data, beskrive mønstre i dem og træffe informerede beslutninger på baggrund af disse mønstre. Statistik forbinder ofte observationer med sandsynlighedsteori for at vurdere usikkerhed i konklusionerne.
Typer af statistik
- Deskriptiv statistik: Opsummerer og visualiserer data (gennemsnit, median, varians, frekvenser, diagrammer).
- Inferential (også kaldet prædiktiv eller statistisk inferens): Trækker konklusioner om en population ud fra en stikprøve ved hjælp af estimater, hypotesetest og konfidensintervaller.
- Explorativ dataanalyse: Undersøger data for mønstre, outliers og antagelser før formelle analyser.
Grundlæggende begreber
- Population vs. stikprøve: Populationen er hele gruppen, man vil sige noget om; en stikprøve er en delmængde, man måler.
- Variabler: Kvalitative (kategoriske) og kvantitative (numeriske) variabler; skalaer som nominal, ordinal, interval og forholdstal.
- Mål for central tendens og spredning: Gennemsnit, median, typetal; varians, standardafvigelse, interkvartilafstand.
- Visualisering: Histogram, søjlediagram, boxplot, spredningsdiagram — vigtige for formidling og fortolkning.
Almindelige metoder og værktøjer
- Sampling: Tilfældig stikprøvetagning, stratificeret sampling, klyngeprøver — for at mindske bias og estimere præcision.
- Hypotesetest: Test af påstande ved hjælp af p-værdier og signifikansniveauer (fx t-test, χ²-test, ANOVA).
- Konfidensintervaller: Angiver usikkerheden på estimater som gennemsnit eller andele.
- Regressionsanalyse: Undersøger sammenhænge mellem variabler (lineær regression, logistisk regression, multivariat analyse).
- Statistisk modelbygning: Valg af variabler, modellens antagelser og validering (cross-validation, residualanalyse).
- Databehandling og software: R, Python (pandas, statsmodels), SPSS, Stata og Excel er almindelige værktøjer til analyser.
Anvendelser i videnskab og samfund
Statistik bruges i mange konkrete sammenhænge:
- Videnskab: Planlægning af eksperimenter, analyse af måledata, vurdering af hypoteser og reproducérbarhed.
- Medicin: Kliniske forsøg, effektevaluering af behandlinger, epidemiologiske studier og risikofaktoranalyser.
- Økonomi: Makroøkonomiske prognoser, regressionsanalyser af markedsdata, paneldata-analyser.
- Psykologi: Skalaudvikling, spørgeskemadata, faktor- og reliabilitetsanalyser.
- Politik og samfund: Meningsmålinger, valgprognoser, policy-evalueringer og analyser af administrative data.
- Markedsføring: Segmentering, A/B-testning, kundeadfærdsanalyse og salgsprognoser.
Fortolkning: korrelation vs. kausalitet
En vigtig forsigtighed i statistik er, at korrelation ikke nødvendigvis betyder årsagssammenhæng. Observationsstudier kan fremvise sammenhænge, men for at bevise kausalitet kræves typisk kontrollerede eksperimenter eller robuste design (randomisering, natural experiments, instrumentvariabler osv.).
Fejlkilder og etik
- Bias: Systematiske fejl i indsamling eller udvælgelse af data (fx selektionsbias, målefejl).
- Overfitting: En model kan passe meget godt til træningsdata, men generaliserer dårligt til nye data.
- Misledende visualisering: Forkert skala eller ufuldstændige data kan give et falskt indtryk.
- Etik og privatliv: Beskyttelse af persondata, transparens i metoder og ansvarlig rapportering er afgørende—særligt i forskning og offentlige beslutninger.
Praktiske eksempler
- Et lands statistiske kontor bruger stikprøver til at estimere arbejdsløshed og befolkningsfordeling.
- Et lægemiddelfirma gennemfører randomiserede kontrollerede forsøg for at teste en ny behandling og anvender konfidensintervaller og p‑værdier til vurdering af effekt.
- En virksomhed kører A/B-tests på to versioner af en hjemmeside for at maksimere konverteringsraten og bruger statistisk inferens til at vælge vinder‑versionen.
Afsluttende bemærkninger
Statistik er både praktisk og teoretisk: praktisk i anvendelsen til at træffe beslutninger på usikker baggrund, og teoretisk i udviklingen af metoder til korrekt inferens. En god statistisk praksis kombinerer korrekt dataindsamling, passende metoder, gennemsigtig rapportering og kritisk fortolkning af resultaterne.
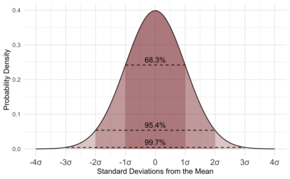
Normalfordelingen i statistik
Historie
De første kendte statistikker er folketællingsdata. Babylonierne foretog en folketælling omkring 3500 f.Kr., egypterne omkring 2500 f.Kr. og de gamle kinesere omkring 1000 f.Kr.
Fra det 16. århundrede udviklede matematikere som Gerolamo Cardano sandsynlighedsteorien, som gjorde statistik til en videnskab. Siden da har folk indsamlet og studeret statistikker om mange ting. Træer, søstjerner, stjerner, sten, ord, næsten alt, der kan tælles, har været genstand for statistik.
Indsamling af data
Før vi kan beskrive verden med statistik, skal vi indsamle data. De data, som vi indsamler i statistikken, kaldes målinger. Når vi har indsamlet data, bruger vi et eller flere tal til at beskrive hver observation eller måling. Lad os f.eks. antage, at vi ønsker at finde ud af, hvor populært et bestemt tv-program er. Vi kan udvælge en gruppe mennesker (kaldet en stikprøve) ud af den samlede befolkning af seere. Derefter spørger vi hver enkelt seer i stikprøven, hvor ofte de ser programmet. Stikprøven er data, som man kan se, og populationen er data, som man ikke kan se (hvis vi antager, at ikke alle seere i populationen bliver spurgt). Et andet eksempel: Hvis vi ønsker at vide, om et bestemt lægemiddel kan hjælpe med at sænke blodtrykket, kan vi give lægemidlet til folk i et stykke tid og måle deres blodtryk før og efter.
Beskrivende og inferentialstatistik
Tal, der beskriver de data, man kan se, kaldes beskrivende statistik. Tal, der giver forudsigelser om de data, man ikke kan se, kaldes inferentialstatistik.
Deskriptiv statistik indebærer, at man bruger tal til at beskrive dataenes karakteristika. F.eks. er gennemsnitshøjden for kvinder i USA en beskrivende statistik: den beskriver en egenskab (gennemsnitshøjden) ved en population (kvinder i USA).
Når resultaterne er blevet opsummeret og beskrevet, kan de bruges til forudsigelse. Dette kaldes inferentialstatistik. Som eksempel kan nævnes, at størrelsen af et dyr afhænger af mange faktorer. Nogle af disse faktorer styres af miljøet, men andre er arvelige. En biolog kan derfor lave en model, der siger, at der er stor sandsynlighed for, at afkommet vil være lille i størrelse - hvis forældrene var små i størrelse. Denne model gør det sandsynligvis muligt at forudsige størrelsen på bedre måder end ved at gætte tilfældigt. Afprøvning af, om et bestemt lægemiddel kan bruges til at helbrede en bestemt tilstand eller sygdom, sker normalt ved at sammenligne resultaterne fra personer, der får lægemidlet, med dem, der får placebo.
Metoder
Oftest indsamler vi statistiske data ved at lave undersøgelser eller eksperimenter. En meningsmåling er f.eks. en slags undersøgelse. Vi udvælger et lille antal personer og stiller dem spørgsmål. Derefter bruger vi deres svar som data.
Valget af, hvilke personer der skal deltage i en undersøgelse eller dataindsamling, er vigtigt, da det har direkte indflydelse på statistikkerne. Når statistikkerne er udarbejdet, kan det ikke længere bestemmes, hvilke personer der er taget med. Lad os antage, at vi ønsker at måle vandkvaliteten i en stor sø. Hvis vi tager prøver ved siden af spildevandsafløbet, vil vi få andre resultater, end hvis prøverne tages på et fjerntliggende og svært tilgængeligt sted i søen.
Der er to slags problemer, der ofte opstår, når der tages prøver:
- Hvis der er mange stikprøver, vil stikprøverne sandsynligvis ligge meget tæt på, hvad de er i den virkelige population. Hvis der derimod er meget få stikprøver, kan de være meget forskellige fra den virkelige population. Denne fejl kaldes en tilfældighedsfejl (se også fejl og residualer i statistik).
- De personer, der indgår i prøverne, skal vælges med omhu. Normalt vil de blive udvalgt tilfældigt. Hvis dette ikke er tilfældet, kan stikprøverne være meget forskellige fra den samlede population. Dette gælder også, selv om der udtages et stort antal stikprøver. Denne form for fejl kaldes bias.
Fejl
Vi kan reducere tilfældige fejl ved at tage en større stikprøve, og vi kan undgå en vis skævhed ved at vælge tilfældigt. Men nogle gange er det svært at tage store tilfældige stikprøver. Og der kan opstå skævheder, hvis forskellige personer ikke bliver spurgt eller nægter at besvare vores spørgsmål, eller hvis de ved, at de får en falsk behandling. Disse problemer kan være svære at løse. Se standardfejl for at få mere at vide.
Beskrivende statistik
Finde midten af dataene
Den midterste del af dataene kaldes et gennemsnit. Gennemsnittet fortæller os om et typisk individ i populationen. Der er tre slags gennemsnit, som ofte anvendes: middelværdien, medianen og modus.
I nedenstående eksempler anvendes disse eksempeldata:
| Navn | A | B | C | D | E | F | G | H | I | J |
| Score | 23 | 26 | 49 | 49 | 57 | 64 | 66 | 78 | 82 | 92 |
Gennemsnitlig
Formlen for middelværdien er
Hvor 

Det betyder, at man beregner middelværdien ved at lægge alle værdierne sammen og derefter dividere med antallet af værdier. I eksemplet ovenfor er gennemsnittet:
Problemet med middelværdien er, at den ikke fortæller noget om, hvordan værdierne er fordelt. Værdier, der er meget store eller meget små, ændrer middelværdien meget. I statistikken kan disse ekstreme værdier være målefejl, men nogle gange indeholder populationen virkelig disse værdier. Hvis der f.eks. er 10 personer i et rum, der tjener 10 $ om dagen, og 1 person, der tjener 1.000.000 $ om dagen. Gennemsnittet af dataene er 90 918 $ pr. dag. Selv om det er det gennemsnitlige beløb, er gennemsnittet i dette tilfælde ikke det beløb, som en enkelt person tjener, og er derfor ikke særlig nyttigt til nogle formål.
Det ovenfor beskrevne gennemsnit er det "aritmetiske gennemsnit". Andre typer er nyttige til visse formål.
Median
Medianen er den midterste del af dataene. For et givet data 

Som et andet eksempel, ligesom det indkomsteksempel, der blev præsenteret for gennemsnittet, kan man overveje et rum med 10 personer, der har indkomster på 10, 20, 20, 20, 40, 50, 60, 90, 90, 100 og 1.000.000 dollars. Her er medianen 55 dollars, fordi 55 dollars er gennemsnittet af de to midterste tal, 50 dollars og 60 dollars. Hvis man ser bort fra ekstremværdien på 1 000 000 $, er middelværdien 53 $. I dette tilfælde er medianen tæt på den værdi, der opnås, når ekstremværdien udelades. Medianen løser problemet med ekstreme værdier som beskrevet i definitionen af middelværdi ovenfor.
Tilstand
Mode er den mest hyppige data. F.eks. er det mest almindelige bogstav på engelsk bogstavet "e". Vi ville sige, at "e" er den højeste værdi af fordelingen af bogstaverne.
Et andet eksempel: Hvis der er 10 personer i et rum med indkomster på 10 $, 20 $, 20 $, 20 $, 40 $, 50 $, 60 $, 90 $, 90 $, 90 $, 90 $, 100 $ og 1.000.000 $, så er modus 90 $, fordi 90 $ forekommer tre gange, og alle andre værdier forekommer mindre end tre gange.
Der kan være mere end én tilstand. Hvis der f.eks. er 10 personer i et rum med indkomster på 10 $, 20 $, 20 $, 20 $, 20 $, 50 $, 60 $, 90 $, 90 $, 90 $, 90 $, 100 $ og 1.000.000 $, er moduserne 20 $ og 90 $. Dette er bi-modalt, eller har to modus. Bi-modalitet er meget almindeligt, og det indikerer ofte, at dataene er en kombination af to forskellige grupper. F.eks. har gennemsnitshøjden for alle voksne i USA en bi-modal fordeling. Det skyldes, at mænd og kvinder har separate gennemsnitshøjder på 1,763 m (5 ft 9 + 1⁄2 in) for mænd og 1,622 m (5 ft 4 in) for kvinder. Disse toppe er tydelige, når begge grupper kombineres.
Mode er den eneste form for gennemsnit, der kan anvendes til data, som ikke kan ordnes.
Finde spredningen af dataene
En anden ting, vi kan sige om et datasæt, er, hvor spredt det er. En almindelig måde at beskrive spredningen af et datasæt på er standardafvigelsen. Hvis standardafvigelsen for et datasæt er lille, ligger de fleste af dataene meget tæt på gennemsnittet. Hvis standardafvigelsen derimod er stor, er mange af dataene meget forskellige fra gennemsnittet.
Standardafvigelsen for en stikprøve er generelt forskellig fra standardafvigelsen for den oprindelige population . Derfor skriver vi 

Hvis dataene følger det almindelige mønster, der kaldes normalfordelingen, er det meget nyttigt at kende standardafvigelsen. Hvis dataene følger dette mønster (vi vil sige, at dataene er normalfordelte), vil ca. 68 ud af hver 100 data afvige mindre end standardafvigelsen fra gennemsnittet. Ikke kun det, men ca. 95 ud af 100 målinger vil afvige fra gennemsnittet med mindre end to gange standardafvigelsen, og ca. 997 ud af 1000 vil ligge tættere på gennemsnittet med mindre end tre standardafvigelser.
Andre beskrivende statistikker
Vi kan også bruge statistik til at finde ud af, at en vis procentdel, procentdel, antal eller brøkdel af mennesker eller ting i en gruppe gør noget eller passer ind i en bestemt kategori.
For eksempel har samfundsforskere brugt statistikker til at finde ud af, at 49 % af verdens befolkning er mænd.
Relateret software
For at støtte statistikere er der blevet udviklet mange statistiske programmer:
- MATLAB
- R
- SAS Institute
- SPSS (fremstillet af IBM)
Spørgsmål og svar
Spørgsmål: Hvad er statistik?
A: Statistik er en gren af den anvendte matematik, der beskæftiger sig med indsamling, organisering, analyse, læsning og præsentation af data.
Spørgsmål: Hvad er de to typer statistik?
A: De to typer statistik er beskrivende og inferentielle statistikker. Deskriptiv statistik giver oversigter over data, mens inferentiel statistik giver forudsigelser.
Spørgsmål: Hvordan hjælper statistik på andre områder?
A: Statistik er en hjælp i forbindelse med undersøgelse af mange andre områder som f.eks. videnskab, medicin, økonomi, psykologi, politik og markedsføring.
Spørgsmål: Hvem arbejder inden for statistik?
Svar: En person, der arbejder inden for statistik, kaldes en statistiker.
Spørgsmål: Hvad betyder ordet "statistik"?
A: Ud over at være navnet på et forskningsområde kan ordet "statistik" også betyde tal, der bruges til at beskrive data eller sammenhænge.
Spørgsmål: Hvilke aktiviteter beskæftiger statistikere sig med?
A: Statistikere beskæftiger sig med aktiviteter som indsamling, organisering, analyse, læsning og præsentation af data.
Søge

