Multiplikation
Multiplikation er en aritmetisk operation til at finde produktet af to tal. Multiplikation er den tredje operation i matematik efter addition, som er den første, subtraktion, som er den anden, og så er der multiplikation.
Med naturlige tal fortæller det dig antallet af fliser i et rektangel, hvor et af de to tal er lig med antallet af fliser på den ene side og det andet tal er lig med antallet af fliser på den anden side.
Med reelle tal giver den dig arealet af et rektangel, hvor det første tal er lig med størrelsen af den ene side og det andet tal er lig med størrelsen af den anden side.
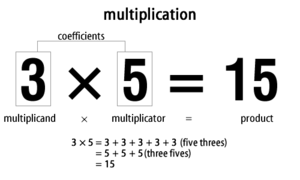
F.eks. er tre ganget med fem summen af fem treere lagt sammen eller summen af tre femmere. Dette kan skrives ned som 3 × 5 = 15, eller tales som "tre gange fem er lig med femten". Matematikere kalder de to tal, som du ønsker at gange, for "koefficienter" sammen eller "multiplikand" og "multiplikator" hver for sig. Multiplikand × multiplikator = produkt.
Multiplikation mellem tal siges at være kommutativ - når rækkefølgen af tallene ikke påvirker værdien af produktet. Dette gælder for de hele tal (hele tal), f.eks. er 4 × 6 det samme som 6 × 4, og også for de rationale tal (brøker) og for alle de andre reelle tal (der kan repræsenteres som et felt på den kontinuerte linje) og også for komplekse tal (tal, der kan repræsenteres som et felt i planen). Det gælder ikke for kvaternioner (tal, der kan repræsenteres som en ring i det firedimensionelle rum), vektorer eller matricer.
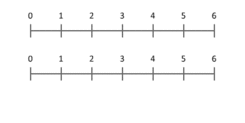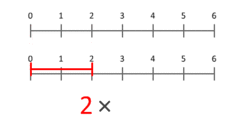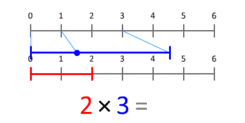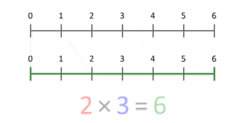
Definitionen af multiplikation som gentagen addition giver mulighed for at nå frem til en mængdeteoretisk fortolkning af multiplikation af kardinaltal. En mere præcis fremstilling er at betragte den som en skalering af mængder. Denne animation viser, at 3 ganges med 2, hvilket giver 6 som resultat. Bemærk, at den blå prik i det blå segment af længde 3 er placeret på position 1, og at det blå segment er skaleret, så denne prik er placeret for enden af det røde segment af længde 2. Ved multiplikation med et vilkårligt X vil den blå prik altid starte ved 1 og slutte ved X. Dette gælder også for X, der er mindre end 1 eller negativt.
Det modsatte af multiplikation er division.
Multiplikationstabel
Lærere kræver normalt, at eleverne skal lære tabellen med de første 9 tal udenad, når de underviser i multiplikation.
| Tabel med 6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Multiplikationstabel | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Relaterede sider
- Tilføjelse
- Kvadratisk nummer
- Subtraktion
Spørgsmål og svar
Q: Hvad er multiplikation?
A: Multiplikation er en aritmetisk operation til at finde produktet af to tal i matematikken. Den repræsenteres ofte ved symboler som × og ⋅.
Spørgsmål: Hvad hedder de to tal, der skal ganges?
Svar: De to tal, der skal multipliceres, kaldes "koefficienter" eller "multiplikand" og "multiplikator" hver for sig.
Spørgsmål: Er multiplikation kommutativ?
Svar: Ja, multiplikation mellem tal siges at være kommutativ - når rækkefølgen af tallene ikke påvirker værdien af produktet. Dette gælder for hele tal, rationale tal, reelle tal og komplekse tal. Det gælder dog ikke for kvaternioner, vektorer og matricer.
Spørgsmål: Hvordan kan vi fortolke multiplikation af kardinaltal?
Svar: Vi kan fortolke multiplikation af kardinaltal som skaleringsmængder - når et tal (multiplikanden) skaleres, så et punkt placeret på position 1 ender i et bestemt punkt (multiplikatoren).
Spørgsmål: Hvordan repræsenterer man tre ganget med fem?
Svar: Tre ganget med fem kan skrives som 3 × 5 = 15, eller sagt som "tre gange fem er lig med femten".
Spørgsmål: Hvad er det modsatte af multiplikation?
Svar: Det modsatte af multiplikation er division.
Søge