Lysets hastighed
Lysets hastighed i det tomme rum er en universel fysisk konstant. Det betyder, at den er den samme overalt i det tomme rum og ikke ændrer sig med tiden. Fysikere bruger ofte bogstavet c til at betegne lysets hastighed i det tomme rum (vakuum). Den er pr. definition præcis 299 792 458 meter i sekundet (983 571 056 fod i sekundet). En foton (en lyspartikel) bevæger sig med denne hastighed i et vakuum.
Ifølge den specielle relativitetsteori er c den maksimale hastighed, hvormed al energi, stof og fysisk information i universet kan bevæge sig. Det er hastigheden for alle masseløse partikler som f.eks. fotoner og tilhørende felter - herunder elektromagnetisk stråling som f.eks. lys - i et vakuum.
Den nuværende teori forudsiger, at den er gravitationshastigheden (dvs. gravitationsbølger). Sådanne partikler og bølger bevæger sig med c uanset kildens bevægelse eller observatørens inertiale referenceramme. I relativitetsteorien er c forbundet med rum og tid og indgår i den berømte ligning for masse-energiækvivalens E = mc 2.
Den specielle relativitetsteori er baseret på den forudsigelse, som hidtil er blevet bekræftet af observationer, at den målte lyshastighed i et vakuum er den samme, uanset om lyskilden og måleren bevæger sig i forhold til hinanden eller ej. Dette udtrykkes undertiden som "lysets hastighed er uafhængig af referencerammen".
Eksempel
Denne adfærd adskiller sig fra vores almindelige forestillinger om bevægelse, som det fremgår af dette eksempel:
George står på jorden ved siden af nogle togskinner (jernbaner). Der kører et tog forbi med en hastighed på 48 km/t (30 mph). George kaster en baseball med 140 km/t (90 mph) i den retning, som toget kører. Tom, en passager i toget, har et apparat (som en radarpistol) til at måle kasteshastigheden. Fordi Tom befinder sig i toget, bevæger han sig allerede med 48 km/t i kastets retning, så Tom måler boldens hastighed som kun 97 km/t.
Med andre ord afhænger baseballens hastighed, som Tom måler den i toget, af togets hastighed.
I eksemplet ovenfor bevægede toget sig med 1/3 af kuglens hastighed, og kuglens hastighed målt i toget var 2/3 af kasthastigheden målt på jorden.
Gentag nu forsøget med lys i stedet for en baseball; det vil sige, at George har en lommelygte i stedet for at kaste en baseball. George og Tom har begge apparater, der er ens til at måle lysets hastighed (i stedet for radarpistolen i baseballeksemplet).
George står på jorden ved siden af nogle togskinner. Der kører et tog forbi med 1/3 af lysets hastighed. George blinker med en lysstråle i den retning, som toget bevæger sig. George måler lysets hastighed som 186.282 miles pr. sekund (299.792 kilometer pr. sekund). Tom, en passager i toget, måler lysstrålens hastighed. Hvilken hastighed måler Tom?
Intuitivt kan man tænke, at hastigheden af lyset fra lommelygten, som målt i toget, burde være 2/3 af den hastighed, der blev målt på jorden, ligesom hastigheden af baseballens hastighed var 2/3. Men i virkeligheden er den hastighed, der måles på toget, den fulde værdi, nemlig 186.282 miles i sekundet (299.792 kilometer i sekundet), ikke 124.188 miles i sekundet (199.861 kilometer i sekundet).
Det lyder umuligt, men det er det, man måler. En del af årsagen er, at lys er energi, som handler og bevæger sig på en helt anden måde end materie eller faste genstande som f.eks. en baseball.
Maxwells ligninger forudsagde lysets hastighed og bekræftede Michael Faradays idé om, at lys var en elektromagnetisk bølge (en måde, hvorpå energi bevæger sig). Ud fra disse ligninger finder vi, at lysets hastighed er relateret til den omvendte af kvadratroden af det frie rums permittivitet ε 0og det frie rums permeabilitet μ 0:
c = 1 ε 0 μ 0 . {\displaystyle c={\frac {1}{\sqrt {\varepsilon _{0}\mu _{0}}}}\ . } 
En konsekvens af denne kendsgerning er, at intet kan gå hurtigere end lysets hastighed. En anden konsekvens er, at for objekter med masse vil et objekt, uanset hvor meget energi der bruges til at øge dets hastighed, komme tættere og tættere på, men det vil aldrig nå lysets hastighed. Disse idéer blev opdaget i begyndelsen af 1900-tallet af Albert Einstein, hvis arbejde fuldstændig ændrede vores forståelse af lys.
Brydningsindekset for et klart materiale er forholdet mellem lysets hastighed i et vakuum og lysets hastighed i det pågældende materiale.
Måling
Rømer
Ole Christensen Rømer brugte en astronomisk måling til at foretage det første kvantitative skøn over lysets hastighed. Målt fra Jorden er perioderne for måner, der kredser om en fjern planet, kortere, når Jorden nærmer sig planeten, end når Jorden fjerner sig fra den. Den afstand, som lyset tilbagelægger fra planeten (eller dens måne) til Jorden, er kortere, når Jorden befinder sig på det punkt i sin bane, der er tættest på planeten, end når Jorden befinder sig på det fjerneste punkt i sin bane, idet afstandsforskellen er diameteren af Jordens bane omkring Solen. Den observerede ændring i månens omløbstid er faktisk forskellen i den tid, det tager lyset at tilbagelægge den kortere eller længere afstand. Rømer observerede denne effekt for Jupiters inderste måne Io, og han udledte heraf, at lyset bruger 22 minutter på at krydse diameteren af Jordens bane.
Bradley
En anden metode er at bruge lysets aberration, som blev opdaget og forklaret af James Bradley i det 18. århundrede. Denne effekt er resultatet af en vektoraddition af lysets hastighed, der kommer fra en fjern kilde (f.eks. en stjerne), og observatørens hastighed (se diagrammet til højre). En observatør, der bevæger sig, ser således lyset komme fra en lidt anden retning og ser derfor kilden i en position forskudt fra sin oprindelige position. Da Jordens hastighedsretning ændrer sig løbende, når Jorden kredser om Solen, medfører denne effekt, at stjernernes tilsyneladende position flytter sig rundt. Ud fra vinkelforskellen i stjernernes position er det muligt at udtrykke lysets hastighed i form af Jordens hastighed omkring Solen. Dette kan med den kendte længde af et år let omregnes til den tid, der er nødvendig for at rejse fra Solen til Jorden. I 1729 brugte Bradley denne metode til at udlede, at lyset rejste 10 210 gange hurtigere end Jorden i dens bane (det moderne tal er 10 066 gange hurtigere), eller tilsvarende, at det ville tage lyset 8 minutter og 12 sekunder at rejse fra Solen til Jorden.
Moderne
I dag måles "lystiden pr. afstandsenhed" - den omvendte værdi af c (1/c), udtrykt i sekunder pr. astronomisk enhed - ved at sammenligne den tid, som radiosignaler tager for at nå forskellige rumfartøjer i solsystemet. Rumfartøjernes position beregnes ud fra solens og de forskellige planeters tyngdekraft. Ved at kombinere mange af disse målinger fås en værdi for lystiden pr. afstandsenhed, der passer bedst muligt. I 2009[opdatering] er det bedste skøn, som er godkendt af Den Internationale Astronomiske Union (IAU), som følger:
lystid pr. afstandsenhed: 499.004783836(10) s
c = 0,0020020039888880410(4) AU/s
c = 173,144632674(3) AU/dag.
Den relative usikkerhed i disse målinger er 0,02 dele pr. milliard (2×10−11 ), hvilket svarer til usikkerheden i jordbaserede målinger af længden ved interferometri. Da meteren er defineret som den længde, der tilbagelægges af lyset i et bestemt tidsinterval, kan målingen af lystiden for en afstandsenhed også fortolkes som en måling af længden af en AU i meter. Meteren betragtes som en enhed for egentlig længde, mens AU ofte anvendes som en enhed for observeret længde i en given referenceramme.
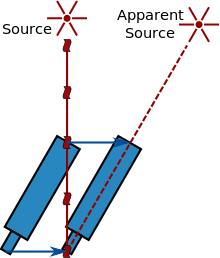
Aberration af lys: Lys fra en fjern kilde ser ud til at komme fra et andet sted for et teleskop i bevægelse på grund af lysets begrænsede hastighed.
Praktiske virkninger
Lysets begrænsede hastighed er en stor hindring for langdistancerejser i rummet. Hvis man antager, at en rejse til den anden side af Mælkevejen ville tage i alt ca. 200.000 år for en besked og dens svar. Endnu mere alvorligt er det, at intet rumfartøj kan rejse hurtigere end lyset, så al transport i galaktisk skala ville i realiteten være ensrettet og ville tage meget længere tid, end nogen moderne civilisation har eksisteret.
Lysets hastighed kan også være et problem på meget korte afstande. I supercomputere sætter lysets hastighed en grænse for, hvor hurtigt data kan sendes mellem processorer. Hvis en processor arbejder med 1 gigahertz, kan et signal højst bevæge sig ca. 30 centimeter på en enkelt cyklus. Processorer skal derfor placeres tæt på hinanden for at minimere kommunikationsforsinkelser; dette kan give problemer med køling. Hvis clockfrekvenserne fortsætter med at stige, vil lysets hastighed i sidste ende blive en begrænsende faktor for det interne design af enkelte chips.
Spørgsmål og svar
Spørgsmål: Hvad er lysets hastighed?
A: Lysets hastighed, der betegnes med "c", er en fysisk konstant, der er præcis 299 792 458 meter i sekundet (983 571 056 fod i sekundet).
Sp: Hvordan repræsenteres lysets hastighed?
A: Lysets hastighed betegnes normalt med "c", og i vakuummedier betegnes den specifikt som "c^0".
Spørgsmål: Hvilke partikler bevæger sig med lysets hastighed?
Svar: Fotoner (lyspartikler) bevæger sig med denne hastighed i et vakuum. Desuden bevæger alle masseløse partikler som f.eks. fotoner og tilhørende felter - herunder elektromagnetisk stråling som lys - sig med c uanset deres kilde eller observatørens inertiale referenceramme.
Sp: Hvad siger den specielle relativitetsteori om lysets hastighed?
Svar: Ifølge den specielle relativitetsteori er c den maksimale hastighed, hvormed al energi, stof og fysisk information kan bevæge sig i universet. Den siger også, at den målte lyshastighed i et vakuum forbliver uændret, uanset om enten lyskilden eller observatøren bevæger sig i forhold til hinanden.
Spørgsmål: Hvordan hænger c sammen med rum og tid?
Svar: I relativitetsteorien er c forbundet med rum og tid ved at optræde i Einsteins berømte ligning E = mc2. Denne ligning viser, hvordan energi kan omdannes til masse og omvendt.
Spørgsmål: Er der beviser, der understøtter den specielle relativitetsteori's forudsigelse om den målte lyshastighed?
A: Ja - indtil videre har observationer bekræftet denne forudsigelse, at uanset hvilken referenceramme den observeres fra, eller hvilken kilde den bevæger sig med, forbliver den målte hastighed konstant.
