π (pi) — Den matematiske konstant: forholdet mellem omkreds og diameter
Opdag π (pi): den fascinerende matematiske konstant, der forbinder en cirkels omkreds og diameter — irrationel, uendelig og afgørende i matematik og natur.
π (/paɪ/) er en matematisk konstant, som er forholdet mellem en cirkels omkreds og dens diameter. Forholdet giver et tal, og dette tal er altid det samme uanset hvilken cirkel man måler. Tallet begynder med 3,141592653589793… og fortsætter uden ende. Tal som dette kaldes irrationelle tal, fordi de ikke kan skrives som en brøk med hele tal, og deres decimaludvikling er uendelig og ikke-periodisk.
Egenskaber
- Irrationalitet: π kan ikke udtrykkes som en forhold af to hele tal. Dette blev bevist i det 18. århundrede.
- Transcendens: π er ikke blot irrationel, men også transcendental — det vil sige, det er ikke rod af nogen ikke-triviel polynomiel ligning med heltalige koefficienter. Dette blev bevist af Ferdinand von Lindemann i 1882.
- Konstant forhold: Uanset diameteren d for en cirkel, er omkredsen C altid C = π·d (eller C = 2·π·r når r er radius).
Grundlæggende formler
- Omkreds: C = π·d = 2·π·r
- Fladeindhold (areal) af en cirkel: A = π·r²
Nærmeværdier og tilnærminger
Selvom π ikke kan udtrykkes præcist med en endelig brøk, findes der gode tilnærmelser, som ofte bruges i beregninger:
- 22/7 ≈ 3,142857 — en simpel og historisk almindeligt anvendt tilnærmelse.
- 355/113 ≈ 3,14159292035 — en langt mere præcis brøk (gyldig til 7 decimaller).
- Decimaludvikling: 3,14159265358979323846… — moderne computerberegninger har bestemt milliarder og billioner af cifre af π.
Beregning og historiske metoder
Gennem historien har man beregnet π med forskellige metoder:
- Geometriske metoder: Archimedes brugte indskrevne og omskrevne polygoner for at afgrænse værdien for π.
- Uendelige rækker: Matematikere som Leibniz, Euler og Ramanujan udviklede serier, der konvergerer mod π (fx Leibniz' serie π/4 = 1 − 1/3 + 1/5 − 1/7 + …).
- Algoritmer til høje præcisioner: Metoder som Gauss–Legendre og Chudnovsky-algoritmen bruges i dag til at beregne billioner af cifre.
- Monte Carlo: Sandsynlighedsbaserede simuleringer kan estimere π ved stokastiske eksperimenter.
Historie og symbol
Brugen af π som symbol for forholdet mellem omkreds og diameter blev først foreslået af walisiske matematiker William Jones i begyndelsen af 1700-tallet og blev udbredt af Euler. Ideen om konstanten går dog langt tilbage — oldtidens civilisationer som egyptere og babylonere brugte tidlige tilnærmelser til π.
Anvendelser
π optræder overalt i matematik og naturvidenskab:
- Geometri og trigonometri (f.eks. i vinkler målt i radianer: 180° = π rad).
- Fysik — bølgebevægelser, elektromagnetisme, statistik og kvantemekanik indeholder ofte π i formler.
- Ingeniørvidenskab og beregninger af arealer, rumfang og cirkulære bevægelser.
Interessante fakta
- Man fejrer ofte π-dagen den 14. marts (14/3 i dag-måned-format), fordi datoen svarer til de første cifre 3,14.
- Det er ukendt om π er normal i base 10 — det vil sige, om hvert ciffer fra 0 til 9 forekommer lige ofte i dens decimaludvikling; dette er et åbent spørgsmål i matematik.
- Nogle matematikere foretrækker at arbejde med konstanten τ = 2·π og argumenterer for, at visse formler bliver enklere med τ.
Selvom π er et enkelt begreb — forholdet mellem en cirkels omkreds og diameter — rummer det dyb matematisk betydning og forbindelser til mange områder inden for både teori og anvendelser.
Pi er en uendelig række af tal
Grundlæggende oplysninger
Definition
π er almindeligvis defineret som forholdet mellem en cirkels omkreds C og dens diameter d:
Omtrentlig værdi
Pi skrives ofte som π, eller det græske bogstav π som en forkortelse. Pi er også et irrationelt tal, hvilket betyder, at det ikke kan skrives som en brøk ( 
), hvor "a" og "b" er hele tal (hele tal). Det betyder i bund og grund, at de cifre i pi, der står til højre for decimaltallet, går i en uendelighed - uden at gentage sig i et mønster, og at det er umuligt at skrive den nøjagtige værdi af pi som et tal. Pi kan kun tilnærmes eller måles til en værdi, der er tæt nok på til praktiske formål.
En værdi tæt på pi er 3,141592653535897932323846462643... En almindelig brøk nærmer sig pi med 
, hvilket giver ca. 3,14285714. Denne tilnærmelse er 0,04 % fra den sande værdi af pi. Selv om denne tilnærmelse accepteres for det meste af dens anvendelse i det virkelige liv, er brøken 
mere nøjagtig (giver ca. 3,14159292) og kan anvendes, når der er behov for en værdi tættere på pi. Computere kan bruges til at få bedre tilnærmelser af pi.
I marts 2019 beregnede Emma Haruka Iwao værdien af pi til 31,4 trillioner cifre.
Omkredsen af en cirkel er lidt mere end tre gange så lang som dens diameter. Det nøjagtige forhold hedder π .
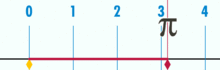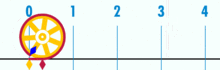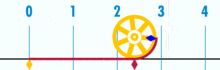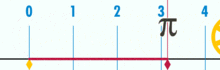
Et diagram, der viser, hvordan π kan findes ved hjælp af en cirkel med en diameter på 1. Omkredsen af denne cirkel er π.
Historie
Matematikere har kendt til pi i tusindvis af år, fordi de har arbejdet med cirkler i lige så lang tid. Civilisationer så gamle som babylonierne har været i stand til at tilnærme pi til mange cifre, f.eks. brøken 25/8 og 256/81. De fleste historikere mener, at de gamle egyptere ikke havde noget begreb om π, og at korrespondancen er et tilfælde.
Den første skriftlige omtale af pi stammer fra år 1900 f.Kr. Omkring 1650 f.Kr. angav egypteren Ahmes en værdi i Rhind-papyrus. Babylonierne kunne finde ud af, at værdien af pi var lidt større end 3 ved at lave en stor cirkel og derefter sætte et stykke reb på omkredsen og diameteren, notere afstandene mellem dem og dividere omkredsen med diameteren.
Kendskabet til tallet pi kom tilbage til Europa og i hænderne på hebræerne, som gjorde tallet vigtigt i et afsnit af Bibelen kaldet Det Gamle Testamente. Herefter var den mest almindelige måde at forsøge at finde pi på at tegne en form med mange sider inden for en hvilken som helst cirkel og bruge arealet af formen til at finde pi. Den græske filosof Archimedes brugte f.eks. en polygonform med 96 sider til at finde værdien af pi, men kineserne kunne i 500 e.Kr. bruge en polygonform med 16 384 sider til at finde værdien af pi. Grækerne, som Anaxagoras af Clazomenae, havde også travlt med at finde ud af andre egenskaber ved cirklen, f.eks. hvordan man laver cirklens kvadrater og kvadrerer tallet pi. Siden da har mange mennesker forsøgt at finde ud af mere og mere nøjagtige værdier af pi.
| En historie om pi | ||
| Filosoffen | Dato | Tilnærmelse |
| omkring 150 e.Kr. | 3.1416 | |
| Zu Chongzhi | 430-501 CE | 3.1415929203 |
| al-Khwarizmi | omkring 800 e.Kr. | 3.1416 |
| al-Kashi | omkring 1430 | 3.14159265358979 |
| Viète | 1540-1603 | 3.141592654 |
| Roomen | 1561-1615 | 3.14159265358979323 |
| Van Ceulen | omkring 1600 | 3.14159265358979323846264338327950288 |
I det 16. århundrede kom der bedre og bedre måder at finde pi på, som f.eks. den komplicerede formel, som den franske jurist François Viète udviklede. Det græske symbol "π" blev for første gang brugt i et essay skrevet i 1706 af William Jones.
En matematiker ved navn Lambert viste også i 1761, at tallet pi var irrationelt, dvs. at det ikke kan skrives som en brøk efter normale standarder. En anden matematiker ved navn Lindeman kunne også i 1882 vise, at pi var en del af den gruppe af tal, der er kendt som transcendenter, som er tal, der ikke kan være løsningen på en polynomiel ligning.
Pi kan også bruges til at beregne mange andre ting end cirkler. Pi's egenskaber har gjort det muligt at bruge det inden for mange andre matematiske områder end geometri, dvs. studiet af former. Nogle af disse områder er kompleks analyse, trigonometri og serier.
Pi i det virkelige liv
Der findes forskellige måder at beregne mange cifre af π på, men det er dog kun af begrænset nytte.
Pi kan undertiden bruges til at beregne arealet eller omkredsen af en cirkel. For at finde omkredsen af en cirkel skal du bruge formlen C (omkreds) = π × (diameter). For at finde arealet af en cirkel skal du bruge formlen π (radius²). Denne formel skrives undertiden som 
, hvor r er variablen for radius af en cirkel og A er variablen for cirklens areal.
At beregne omkredsen af en cirkel med en fejl på 1 mm:
- 4 cifre er nødvendige for en radius på 30 meter
- 10 cifre for en radius svarende til Jordens radius
- 15 cifre for en radius svarende til afstanden fra jorden til solen.
- 20 cifre for en radius svarende til afstanden fra jorden til Polaris.
Man fejrer normalt den 14. marts som Pi-dag, fordi den 14. marts også skrives som 3/14, som repræsenterer de første tre tal 3,14 i tilnærmelsen af pi. Pi-dagen startede i løbet af 2001.
Relaterede sider
- Liste over numre
- Irrationale tal
- Kvadratrod af 2
- Det gyldne snit
- E (matematisk konstant)
- At gøre cirklen til en firkant
- Transcendentalt tal
Spørgsmål og svar
Spørgsmål: Hvad er tallet ً?
A: ً er en matematisk konstant, som er forholdet mellem en cirkels omkreds og dens diameter.
Spørgsmål: Hvad giver det?
A: Det giver et tal, og dette tal er altid det samme.
Spørgsmål: Hvordan starter dette tal?
A: Tallet starter som 3,141592653589793 ... og fortsætter uden ende.
Spørgsmål: Hvilken type tal er dette?
Svar: Disse tal kaldes irrationelle tal.
Sp: Hvad er diameteren på en cirkel?
A: En cirkels diameter er den største kordel, der kan indpasses i den, og som går gennem dens centrum.
Spørgsmål: Hvad er en cirkels omkreds? A: Afstanden omkring en cirkel kaldes dens omkreds.
Spørgsmål: Forbliver pi konstant uanset forskellige cirkler? Svar: Ja, pi er konstant uanset forskellige cirkler, fordi forholdet mellem deres omkreds og diameter altid er det samme.
Søge