Hvad er en cirkel? Definition, radius, diameter, π, omkreds og areal

Lær alt om cirkler: definition, radius, diameter, π, formler og nemme eksempler til beregning af omkreds og areal.

Forfatter: Leandro Alegsa

09-02-2026 19:26

En cirkel er en rund, todimensional form. Alle punkter på kanten af cirklen ligger i samme afstand fra centrum og danner dermed en lukket, glat kurve uden hjørner.

Centrum, radius og diameter

En cirkels radius er en ret linje fra cirklens centrum til et punkt på kanten. Matematikere bruger bogstavet r {\displaystyle r} for længden af radius. En cirkels centrum er punktet i midten af cirklen. Det skrives ofte som O {\displaystyle O} $O$ .

Diameteren (bogstaveligt "hele vejen igennem") er en ret linje, der går fra et punkt på cirklens kant gennem centrum til et punkt på den modsatte side. Matematikere bruger bogstavet d {\displaystyle d} $d$ for længden af diameteren. Diameteren er altid det dobbelte af radius, dvs.

d = 2 r {\displaystyle d=2r} $d=2r$

Omkreds (perimeter)

Omkredsen af en cirkel er den linje, der går hele vejen rundt om figuren. Matematikere skriver ofte omkredsen med bogstavet C {\displaystyle C} $C$ .

Forholdet mellem omkredsen og diameteren er et konstant tal, kaldet π (det græske bogstav pi): π {\displaystyle \pi } $\pi$ = omkreds / diameter. Derfor kan omkredsen også skrives som

C = 2πr — omkredsen i forhold til radius
C = πd — omkredsen i forhold til diameter

Med andre ord: hvis du kender radius r, får du C=2\pi r og hvis du kender diameter d, får du C=\pi d. Disse udtryk bruges ofte i geometri og anvendt matematik.

Hvad er π?

Tallet π {\displaystyle \pi } $\pi$ er et særligt tal: det er irrationelt (kan ikke skrives som en endelig brøk) og transcendental (ikke roden af noget polynomium med heltalskoefficienter). Som brøkdel benyttes ofte tilnærmelser som 22 / 7 {\displaystyle 22/7} $22/7$ eller den mere præcise 355 / 113 {\displaystyle 355/113} $355/113$ . Som decimaltal er π cirka 3,1415926535..., og dens decimaludvikling fortsætter uendeligt uden gentagende mønster.

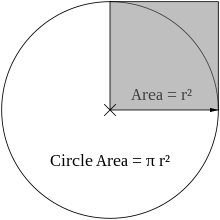
Areal

Arealet inden for en cirkel skrives ofte som A {\displaystyle A} $A$ . Formlen for arealet er:

A = π r² — altså radius ganget med sig selv og derefter ganget med π. I de originale billedsymboler fra teksten:

(A {\displaystyle A} $A$ er lig med π {\displaystyle \pi } $\pi$ gange r {\displaystyle r} gange r {\displaystyle r} ).)

Eksempel: Hvis r = 3 cm, så er arealet A = π · 3² = π · 9 ≈ 28,27 cm² (hvis man bruger π ≈ 3,14159).

Andre vigtige begreber og egenskaber

Bue (arc): En del af cirklens kant mellem to punkter.
Kord (chord): En ret linje mellem to punkter på cirklens kant. Diameteren er en særlig kord, som går gennem centrum.
Sektor: Et arealudsnit af cirklen afgrænset af to radier og den mellemliggende bue (som et stykke af en kage).
Tangent: En linje, der rører cirklen i præcis ét punkt uden at skære igennem den.
Centralvinkel: En vinkel med toppunkt i centrum, som afgrænser en sektor eller en bue; buens længde er proportional med vinklen.

Anvendelser

Cirkler optræder overalt i praksis: hjul, gear, byggeri (buede konstruktioner), arkitektur, astronomi (baner), og inden for matematik og fysik til periodiske bevægelser og bølger. Formlerne for omkreds og areal bruges til beregning af materialeforbrug, omkreds af runde objekter og arealudnyttelse.

Tips til beregning

Hvis du kender diameter d, kan du hurtigt finde radius r = d/2 og derefter bruge arealet A = πr² eller omkredsen C = πd.
Brug passende enheder (f.eks. cm, m). Omkreds har enhed i længde (f.eks. cm), areal i kvadratenheder (f.eks. cm²).
Ved praktiske beregninger kan du bruge π ≈ 3,1416 eller brøknære tilnærmelser som 22/7 afhængigt af krav til nøjagtighed.

Cirklens areal er lig med π {\displaystyle \pi } $\pi$ gange arealet af det grå kvadrat.

En cirkel

Beregning af π

π {\displaystyle \pi } $\pi$ kan måles ved at tegne en cirkel og derefter måle dens diameter ( d {\displaystyle d} $d$ ) og omkreds ( C {\displaystyle C} $C$ ). Dette skyldes, at omkredsen af en cirkel altid er lig med π {\displaystyle \pi } $\pi$ gange dens diameter.

π = C d {\displaystyle \pi ={\frac {C}{d}}} $\pi ={\frac {C}{d}}$

π {\displaystyle \pi } $\pi$ kan også beregnes udelukkende ved hjælp af matematiske metoder. De fleste metoder, der anvendes til at beregne værdien af π {\displaystyle \pi } $\pi$ , har ønskelige matematiske egenskaber. De er dog svære at forstå uden at kende trigonometri og regning. Nogle metoder er dog ret enkle, f.eks. denne form af Gregory-Leibniz-serien:

π = 4 1 - 4 3 + 4 5 - 4 7 + 4 9 - 4 11 ... {\displaystyle \pi ={\frac {4}{1}}}-{\frac {4}{3}}}+{\frac {4}{5}}}-{\frac {4}{7}}}+{\frac {4}{9}}-{\frac {4}{11}}}\,\ldots } $\pi ={\frac {4}{1}}-{\frac {4}{3}}+{\frac {4}{5}}-{\frac {4}{7}}+{\frac {4}{9}}-{\frac {4}{11}}\,\ldots$

Selv om denne serie er let at skrive og beregne, er det ikke let at se, hvorfor den er lig med π {\displaystyle \pi } $\pi$ . En meget nemmere måde at gribe det an på er at tegne en imaginær cirkel med radius r {\displaystyle r} centreret om oprindelsen. Så vil ethvert punkt ( x {\displaystyle x} , y {\displaystyle y} ), hvis afstand d {\displaystyle d} $d$ fra oprindelsen er mindre end r {\displaystyle r} , beregnet ved hjælp af pythagoras' sætning, ligge inden for cirklen:

d = x 2 + y 2 {\displaystyle d={\sqrt {x^{2}+y^{2}}}} $d={\sqrt {x^{2}+y^{2}}}$

Ved at finde et sæt punkter inden for cirklen kan cirklens areal A {\displaystyle A} $A$ estimeres, f.eks. ved at bruge hele koordinater for et stort r {\displaystyle r} . Da arealet A {\displaystyle A} $A$ af en cirkel er π {\displaystyle \pi } $\pi$ gange radius i kvadrat, kan π {\displaystyle \pi } $\pi$ tilnærmes ved hjælp af følgende formel:

π = A r 2 {\displaystyle \pi ={\frac {A}{r^{2}}}} $\pi ={\frac {A}{r^{2}}}$

Beregning af arealet, omkredsen, diameteren og radius af en cirkel

Område

Ved hjælp af dens radius: A = π r 2 {\displaystyle A=\pi r^{2}} $A=\pi r^{2}$

Ved hjælp af dens diameter: A = π d 2 4 {\displaystyle A={{\frac {\pi d^{2}}}{4}}}} $A={\frac {\pi d^{2}}{4}}$

Ved hjælp af dens omkreds: A = C 2 4 π {\displaystyle A={\frac {C^{2}}}{4\pi }}} $A={\frac {C^{2}}{4\pi }}$

Omkreds

Ved hjælp af dens diameter: C = π d {\displaystyle C=\pi d} $C=\pi d$

Ved hjælp af dens radius: C = 2 π r {\displaystyle C=2\pi r} $C=2\pi r$

Ved hjælp af sit område: C = 2 π A {\displaystyle C=2{\sqrt {\pi A}}} $C=2{\sqrt {\pi A}}$

Diameter

Ved hjælp af dens radius: d = 2 r {\displaystyle d=2r} $d=2r$

Ved hjælp af dens omkreds: d = C π {\displaystyle d={\frac {C}{\pi }}} $d={\frac {C}{\pi }}$

Ved hjælp af dens areal: d = 2 A π {\displaystyle d=2{\sqrt {\frac {A}{\pi }}}} $d=2{\sqrt {\frac {A}{\pi }}}$

Radius

Ved hjælp af dens diameter: r = d 2 {\displaystyle r={\frac {d}{2}}}} $r={\frac {d}{2}}$

Ved hjælp af dens omkreds: r = C 2 π {\displaystyle r={\frac {C}{2\pi }}} $r={\frac {C}{2\pi }}$

Ved hjælp af dens areal: r = A π {\displaystyle r={\sqrt {\frac {A}{\pi }}}} $r={\sqrt {\frac {A}{\pi }}}$

Relaterede sider

Halvcirkel
Kugle
At gøre cirklen til en firkant
Pi
Pi (bogstav)
Tau

Spørgsmål og svar

Spørgsmål: Hvad er en cirkel?

A: En cirkel er en rund, todimensionel form. Alle punkter på kanten af cirklen er i samme afstand fra centrum.

Q: Hvad bruger matematikere til at repræsentere længden af en cirkels radius?

A: Matematikere bruger bogstavet r til at angive længden af en cirkels radius.

Spørgsmål: Hvad skrives som O i cirkler?

Svar: Centrum i en cirkel skrives ofte som O.

Sp: Hvor lang er diameteren på en cirkel?

Svar: Diameteren (som betyder "hele vejen igennem") i en cirkel er en lige linje, der går fra den ene side til den modsatte side og lige igennem cirklens centrum. Den er lig med det dobbelte af dens radius (d er lig med 2 gange r).

Sp: Hvilket bogstav bruger matematikere til at repræsentere omkredsen?

A: Matematikere bruger C for omkreds, som betyder "hele vejen rundt".

Spørgsmål: Hvordan kan vi beregne arealet inden for en cirkel?

A: Arealet, A, inden for en cirkel kan beregnes ved at gange dens radius med sig selv og derefter multipliceres med ً (A er lig med ً gange r gange r).

Søge