Molekylære orbitaler (MO): Definition, opbygning og anvendelse

Forstå molekylære orbitaler: definition, opbygning og anvendelse. Lær hvordan MO'er beskriver elektronfordeling, binder atomer og forudsiger molekylers egenskaber — inkl. beregninger og diagrammer.

Forfatter: Leandro Alegsa

14-01-2026 22:08

I kemi beskriver en molekylær orbital (ofte forkortet MO), hvordan elektroner opfører sig, når atomer samles til et molekyle. En MO er en matematisk funktion, som beskriver den bølgelignende natur af en elektron i et molekyle og angiver sandsynligheden for at finde elektroner i et bestemt område. Kemikere bruger sådanne funktioner til at forudsige og forklare både kemiske og fysiske egenskaber af molekyler.

Hvordan dannes molekylære orbitaler?

Molekylære orbitaler kan konstrueres ved at kombinere atomorbitaler fra de indgående atomer — typisk ved metoden kaldet LCAO (lineær kombination af atomorbitaler). Når to eller flere atomorbitaler overlapper, kan de interferere konstruktivt eller destruktivt:

Konstruktiv interferens fører til et bindende (σ eller π) orbital, hvor elektrontætheden mellem atomer øges og sænker energien.
Destruktiv interferens skaber et antibindende (σ* eller π*) orbital, med en nodestruktur (nulpunkter) mellem atomer og højere energi.

Man kan også kombinere hybride orbitaler fra hvert atom eller bruge grupper af allerede dannede molekylære orbitaler ved dannelse af større systemer. Moderne computere løser numerisk for sådanne funktioner, så man kan anvende kvantemekanikken på realistiske molekyler.

Typer af molekylære orbitaler

Sigma (σ) orbitaler: Omdrejningssymmetriske omkring bindingsaksen; opstår ofte ved overlap af s‑ eller pz‑orbitaler langs aksen.
Pi (π) orbitaler: Har en nodalplan langs bindingsaksen; dannes typisk ved side‑til‑side overlap af p‑orbitaler.
Antibindende orbitaler (σ*, π*): Højere i energi og indeholder nodale flader, som reducerer binding mellem atomer.
Ikke‑bindende orbitaler (n): Lokaliserede orbitaler, som hverken fremmer eller svækker binding (typisk lone pairs).

Energirelationer, fyldning og begreber

Orbitalernes relative energier bestemmer, hvordan elektroner fylder dem. To centrale begreber er:

HOMO (Highest Occupied Molecular Orbital) — det højst placerede besatte orbital.
LUMO (Lowest Unoccupied Molecular Orbital) — det lavest placerede ubesatte orbital.

Forskellen mellem HOMO og LUMO (energigabet) er afgørende for et molekyles reaktivitet og optiske egenskaber. Bond order kan beregnes ved at trække antal antibindende elektroner fra antal bindende elektroner og dele med to — dette giver et mål for bindingsstyrken. MO‑teori forklarer også magnetiske egenskaber: f.eks. er oxygen (O2) paramagnetisk, fordi det har ubesatte elektroner i π*‑orbitaler.

Anvendelser og eksempler

Forklaring af simple systemer: I H2 dannes et lavtenergetisk σ(1s) bindende orbital og et højenergetisk σ*(1s) antibindende orbital — H2 får to elektroner i det bindende orbital og er dermed stabilt.
Forklaring af uventede effekter: He2 eksisterer ikke stabilt i gasfasen, fordi begge 1s‑orbitaler resulterer i lige mange bindende og antibindende elektroner.
Spektroskopi og fotokemi: Overgange mellem MO'er (fx HOMO → LUMO) bestemmer absorption og emission af lys.
Organisk kemi: Delokaliserede π‑systemer (f.eks. i benzener) forklares med MO'er, hvilket giver indsigt i stabilitet og reaktivitet.
Katalyse og materialer: MO‑analyse hjælper med at forstå bindingsinteraktioner, elektrontransport og reaktivitet i katalysatorer og halvledende materialer.

Praktiske metoder og beregninger

For komplekse molekyler bygger man ofte matematiske modeller af MO'er og løser Schrödinger‑ligningen numerisk med computere. Afhængigt af krav til nøjagtighed og størrelse af systemet anvendes metoder fra HF (Hartree–Fock) til tæthedsfunktionsmetoder (DFT) og post‑HF korrelationsteknikker. Resultaterne bruges til at forudsige geometrier, bindestyrker, spektrale egenskaber og reaktionsmekanismer ved hjælp af kvantemekanikken.

Vigtige begreber at huske

MO'er er ikke fysiske skaller man kan pege på — de er bølgefunktioner (matematiske beskrivelser) som angiver sandsynligheder.
Overlap og symmetri bestemmer, hvilke atomorbitaler der kan kombinere og i hvilken grad.
Fyldningsregler (Pauli‑princippet og Hunds regel) anvendes også på molekylære orbitaler.

Samlet set gør teorien om molekylære orbitaler det muligt for kemikere at anvende kvantemekanikken til at forstå, beskrive og forudsige et bredt spektrum af kemiske og fysiske egenskaber i molekyler.

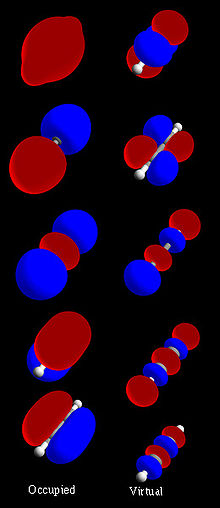
Figur 1: Komplet acetylen (H-C≡C-H) molekylær orbital sæt

Historie

Ordet orbital blev første gang brugt på engelsk af Robert S. Mulliken. Den tyske fysiker Erwin Schrödinger skrev tidligere om MO'er. Schrödinger kaldte dem Eigenfunktion.

Fysikeren Max Born beskrev teorien bag molekylære orbitaler i 1926. I dag er den kendt som Borns regel og er en del af den københavnske fortolkning af kvantemekanikken. Da teorien oprindeligt blev foreslået, var den ikke i overensstemmelse med Niels Bohrs atommodel. Bohrs model beskrev elektroner som "kredsende" om atomkernen, idet de bevægede sig rundt i cirkler. Men Born-modellen vandt efterhånden populær støtte, fordi den kunne beskrive elektronernes placering i molekyler og forklarede en række tidligere uforklarlige kemiske reaktioner.

Oversigt

Atomorbitaler forudsiger placeringen af en elektron i et atom. Molekylære orbitaler opstår, når atomorbitaler bringes sammen. En molekylær orbital kan give oplysninger om et molekyls elektronkonfiguration. Elektronkonfigurationen er den mest sandsynlige position og energien for en (eller et par af) elektron(er). For det meste repræsenteres en MO som en lineær kombination af atomorbitaler (LCAO-MO-metoden), især ved tilnærmet brug. Det betyder, at kemikere antager, at chancen for, at en elektron befinder sig et hvilket som helst sted i molekylet, er summen af sandsynlighederne for, at elektronen befinder sig der på grundlag af de enkelte atomorbitaler. LCAO-MO er en enkel model for bindinger i molekyler og er vigtig for studiet af molekylorbitalteori.

Teoretiske kemikere bruger computere til at beregne MO'erne for forskellige molekyler (både reelle og imaginære). Computeren kan tegne grafer over "skyen" for at vise, hvor sandsynligt det er, at elektronen vil være i et bestemt område. Computerne kan også give oplysninger om molekylets fysiske egenskaber. De kan også sige, hvor meget energi der kræves for at danne molekylet. Dette hjælper kemikere med at sige, om nogle små molekyler kan kombineres til større molekyler.

De fleste af de nuværende metoder til beregningskemi begynder med at beregne MO'erne for et system. Hver MO's elektriske felt genereres af alle atomernes kerner og en gennemsnitlig fordeling af de andre elektroner.

Analogi

At forstå MO'er svarer til at vide, hvor hver enkelt medarbejder befinder sig i et stort byggemarked (uden at kigge ind i butikken). En analytiker kender antallet af medarbejdere i butikken og hver enkelt medarbejders afdeling. Han ved også, at de ansatte ikke træder hinanden over tæerne, og at de ansatte står i gangen i stedet for på hylderne med varerne. Medarbejderne forlader deres egen afdeling for at hjælpe kunderne med at finde varer i andre afdelinger eller for at kontrollere lagerbeholdningen. En analytiker, der angiver alle medarbejdernes placering i butikken på et bestemt tidspunkt uden at se ind i butikken, er som en kemiker, der beregner et molekyls MO'er. Ligesom MOs ikke kan fortælle den nøjagtige placering af hver enkelt elektron, er den nøjagtige placering af hver enkelt medarbejder ikke kendt. En MO, der har et nodalplan, svarer til den konklusion, at de ansatte går ned ad gangene og ikke gennem hylderne. Selv om elektroner bidrager fra et bestemt atom, fylder elektronen en MO uden hensyn til dens kildeatom. Det svarer til, at en medarbejder forlader sin afdeling for at gå et andet sted i butikken i løbet af dagen. Så en MO er en ufuldstændig beskrivelse af en elektron, ligesom analytikerens beregninger om den usynlige butik er et ufuldstændigt gæt om medarbejdernes placering.

At beregne MO'erne svarer til at forudsige placeringen af hver enkelt medarbejder i et byggemarked.

Dannelse af molekylære orbitaler

Teoretiske kemikere har opfundet regler til beregning af MO'er. Disse regler stammer fra en forståelse af kvantemekanikken. Kvantemekanikken hjælper kemikere med at bruge fysikkens oplysninger om elektroner til at regne ud, hvordan elektronerne opfører sig i molekyler. Molekylære orbitaler dannes på baggrund af "tilladte" vekselvirkninger mellem atomorbitaler. (Interaktionerne er "tilladte", hvis atomorbitalernes symmetrier (bestemt ud fra gruppeteori) er forenelige med hinanden). Kemikere studerer atomorbitalernes interaktioner. Disse interaktioner kommer fra overlapningen (et mål for hvor godt to orbitaler interagerer konstruktivt med hinanden) mellem to atomorbitaler. Overlapningen er vigtig, hvis atomorbitalerne ligger tæt på hinanden med hensyn til energi. Endelig skal antallet af MO'er i et molekyle være lig med antallet af atomorbitaler i de atomer, der samles for at danne molekylet.

Kvalitativ tilgang

Kemikere er nødt til at forstå MO'ernes geometri for at kunne diskutere molekylestruktur. LCMO-metoden (Linear combination of atomic orbitals molecular orbital) giver en grov, men god beskrivelse af MO'erne. I denne metode udtrykkes molekylorbitalerne som lineære kombinationer af alle atomorbitalerne for hvert atom i molekylet.

Lineære kombinationer af atomare orbitaler (LCAO)

Molekylære orbitaler blev først introduceret af Friedrich Hund og Robert S. Mulliken i 1927 og 1928.

Den lineære kombination af atomare orbitaler eller "LCAO"-approximation for molekylære orbitaler blev introduceret i 1929 af Sir John Lennard-Jones. Hans banebrydende artikel viste, hvordan man ud fra kvanteprincipper kunne udlede fluor- og oxygenmolekylernes elektroniske struktur. Denne kvalitative tilgang til molekylorbitalteori er en del af starten på den moderne kvantekemi.

Lineære kombinationer af atomorbitaler (LCAO) kan bruges til at gætte de molekylære orbitaler, der dannes, når molekylets atomer bindes sammen. I lighed med en atomorbital kan en Schrodinger-ligning, som beskriver en elektrons adfærd, også konstrueres for en molekylær orbital. Lineære kombinationer af atomorbitaler (summen og forskellen af atomernes bølgefunktioner) giver tilnærmelsesvis løsninger på de molekylære Schrodinger-ligninger. For simple diatomare molekyler er de bølgefunktioner, man får, matematisk repræsenteret ved ligningerne

Ψ = c_a ψ_a + c_b ψ_b

Ψ* = c_a ψ_a - c_b ψ_b

hvor Ψ og Ψ* er de molekylære bølgefunktioner for henholdsvis de bindende og antibindende molekylære orbitaler, ψ_a og ψ_b er de atomare bølgefunktioner fra henholdsvis atom a og b, og c_a og c_b er justerbare koefficienter. Disse koefficienter kan være positive eller negative, afhængigt af energierne og symmetrierne i de enkelte atomorbitaler. Efterhånden som de to atomer kommer tættere på hinanden, overlapper deres atomorbitaler hinanden og skaber områder med høj elektrontæthed. Der dannes således molekylære orbitaler mellem de to atomer. Atomerne holdes sammen af den elektrostatiske tiltrækning mellem de positivt ladede atomkerner og de negativt ladede elektroner, der besætter de bindende molekylære orbitaler.

Bindende, antibindende og ikke-bundende MO'er

Når atomorbitaler interagerer, kan den resulterende molekylære orbital være af tre typer: bindingsorbital, antibindingsorbital eller ikke-bindingsorbital.

Obligatoriske metoder:

Bindingsvekselvirkninger mellem atomorbitaler er konstruktive (i fase) vekselvirkninger.
Bindingsmålinger har en lavere energi end de atomorbitaler, der kombineres for at skabe dem.

Antibonding MO'er:

Antibindende vekselvirkninger mellem atomorbitaler er destruktive (ude af fase) vekselvirkninger.
Antibindende MO'er har en højere energi end de atomare orbitaler, der kombineres for at skabe dem.

Ikke-bundene MO'er:

Ikke-bundende MO'er er resultatet af manglende interaktion mellem atomorbitaler på grund af manglende kompatible symmetrier.
Ikke-bundende MO'er vil have samme energi som atomorbitalerne for et af atomerne i molekylet.

HOMO og LUMO

Hver molekylær orbital har sit eget energiniveau. Kemikere sorterer MO'erne efter energiniveauer. Kemikere antager, at elektronerne vil fylde de MO'er på det laveste energiniveau først. Hvis et molekyle f.eks. har elektroner til at fylde 15 orbitaler, vil de 15 MO'er med de laveste energiniveauer blive fyldt. Den 15. MO på listen vil blive kaldt "højeste besatte molekylære orbital" (HOMO), og den 16. MO på listen vil være "laveste ubesatte molekylære orbital" (LUMO). Forskellen mellem HOMO's energiniveau og LUMO's energiniveau kaldes båndgabet. Bandgabet kan undertiden tjene som et mål for molekylets excitabilitet: jo mindre energien er, jo lettere bliver det exciteret. Når elektronen bliver exciteret, vil den hoppe til et ubesat MO. Dette kan f.eks. hjælpe med at gætte, om noget vil afgive lys (luminescens).

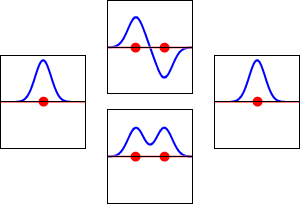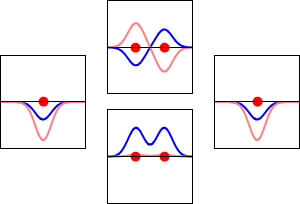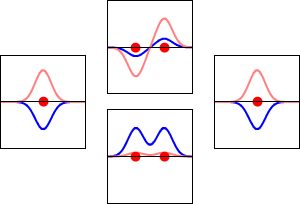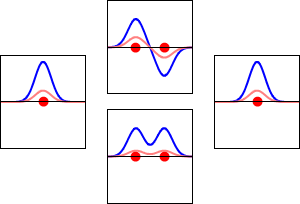
Elektronbølgefunktioner for hydrogenatomets 1s orbital (venstre og højre) og de tilsvarende bindingsorbitaler (nederst) og antibindingsorbitaler (øverst) for H2 -molekylet. Den reelle del af bølgefunktionen er den blå kurve, og den imaginære del er den røde kurve. De røde prikker markerer protonernes placering. Elektronernes bølgefunktion svinger i henhold til Schrödingers bølgeligning, og orbitalerne er dens stående bølger. Den stående bølges frekvens er proportional med orbitalens energi. (Dette plot er et endimensionalt udsnit af det tredimensionale system).

Spørgsmål og svar

Spørgsmål: Hvad er en molekylær orbital?

A: En molekylær orbital (eller MO) er en matematisk funktion, som beskriver en elektrons bølgelignende adfærd i et molekyle. Den forklarer, hvad der sker med elektroner, når atomer slutter sig sammen i et molekyle, og kan fortælle sandsynligheden for at finde en elektron i et bestemt område.

Spørgsmål: Hvordan opbygger kemikere matematiske modeller af molekylære orbitaler?

A: Kemikere opbygger normalt matematiske modeller af molekylære orbitaler ved at kombinere atomorbitaler. Der kan også anvendes hybride orbitaler fra hvert atom i molekylet eller andre molekylære orbitaler fra grupper af atomer. Computere kan arbejde med disse funktioner.

Spørgsmål: Hvad har kvantemekanikken med studiet af molekyler at gøre?

Svar: Molekylære orbitaler gør det muligt for kemikere at anvende kvantemekanikken til at studere molekyler. De besvarer spørgsmål om, hvordan atomerne i molekyler hænger sammen, og giver indsigt i kemiske og fysiske egenskaber.

Sp: Hvad er orbitaldiagrammer?

A: Orbitaldiagrammer er visuelle repræsentationer, der angiver, hvor elektroner sandsynligvis vil være at finde i et atom ud fra dets forskellige afrundede former.

Sp: Hvordan fungerer hybridorbitaler?

Svar: Hybridorbitaler kombinerer forskellige typer atomorbitaler til en ny type, som har unikke egenskaber i forhold til de enkelte dele. Disse hybrider anvendes ofte ved opbygning af matematiske modeller for molekylære orbitaler.

Spørgsmål: Hvordan kan computere hjælpe med at studere MO'er?

Svar: Computere kan hjælpe med at studere MO'er ved at arbejde med deres funktioner og give mere præcise forudsigelser eller forklaringer på kemiske og fysiske egenskaber i molekyler.

Søge