Bandgab | energiområde i et fast stof, hvor der ikke kan eksistere nogen elektrontilstande

Inden for halvlederfysik

Forskere bruger båndgabet til at forudsige, om et fast stof vil lede elektricitet. De fleste elektroner (kaldet valenselektroner) er tiltrukket af kernen på kun ét atom. Men hvis en elektron har energi nok til at flyve væk fra den nærmeste kerne, kan den deltage i strømmen af elektrisk strøm på tværs af de mange atomer, der udgør det faste stof. De elektroner, der ikke er tæt knyttet til kun én kerne, kaldes ledningsbåndet.

I halvledere og isolatorer viser kvantemekanikken, at elektroner kun findes i et antal energibånd. Elektroner er forbudt fra andre energiniveauer. Udtrykket båndgab henviser til energiforskellen mellem toppen af valensbåndet og bunden af ledningsbåndet. Elektroner er i stand til at springe fra et bånd til et andet. En elektron skal dog have en vis mængde energi for at springe fra et valensbånd til et ledningsbånd. Den nødvendige energimængde varierer fra materiale til materiale. Elektroner kan få energi nok til at hoppe til ledningsbåndet ved at absorbere enten en fonon (varme) eller en foton (lys).

En halvleder er et materiale med et lille, men ikke-nul båndgab, som opfører sig som en isolator ved absolut nulpunktstemperatur (0 K), men som tillader varme at ophidse elektroner nok til at hoppe ind i ledningsbåndet ved temperaturer under smeltepunktet. I modsætning hertil er et materiale med et stort båndgab en isolator. I ledere kan valensbåndet og ledningsbåndet overlappe hinanden, så de har ikke nødvendigvis et båndgab.

Ledningsevnen for intrinsiske halvledere er stærkt afhængig af båndgabet. De eneste ledningsbærere, der er til rådighed, er de elektroner, som har tilstrækkelig termisk energi til at blive exciteret over båndgabet.

Båndgabteknik er processen med at kontrollere eller ændre et materiales båndgab ved at kontrollere sammensætningen af visse halvlederlegeringer, såsom GaAlAs, InGaAs og InAlAs. Det er også muligt at konstruere lagdelt materiale med skiftende sammensætninger ved hjælp af teknikker som molekylærstråleepitaxi. Disse metoder anvendes til konstruktion af HBT'er (heterojunction bipolære transistorer), laserdioder og solceller.

Det er svært at trække en grænse mellem halvledere og isolatorer. En måde er at betragte halvledere som en type isolator med et smalt båndgab. Isolatorer med et større båndgab, som regel større end 3 eV, hører ikke til gruppen af halvledere og udviser generelt ikke halvledende adfærd under praktiske forhold. Elektronmobilitet spiller også en rolle ved bestemmelsen af et materiales uformelle gruppering som halvleder.

Halvlederes båndgabsenergi har tendens til at falde med stigende temperatur. Når temperaturen stiger, øges amplituden af atomvibrationerne, hvilket fører til større interatomare afstand. Interaktionen mellem gitterfononerne og de frie elektroner og huller vil også påvirke bandgabet en smule. Forholdet mellem bandgap-energien og temperaturen kan beskrives ved Varshnis empiriske udtryk,

E g ( T ) = E g ( 0 ) - α T 2 T + β {\displaystyle E_{g}(T)=E_{g}(0)-{\frac {\alpha T^{2}}}{T+\beta }}} , hvor E_g (0), α og β er materialekonstanter.

I en almindelig halvlederkrystal er båndgabet fast på grund af kontinuerlige energitilstande. I en kvantepunktkrystal er båndgabet størrelsesafhængigt og kan ændres for at frembringe et spektrum af energier mellem valensbåndet og ledningsbåndet. Det er også kendt som kvantebegrænsningseffekten.

Bandgaps afhænger også af trykket. Bandgab kan være enten direkte eller indirekte, afhængigt af den elektroniske båndstruktur.

Matematisk fortolkning

Klassisk er forholdet mellem sandsynlighederne for, at to tilstande med en energiforskel ΔE vil blive besat af en elektron, givet ved Boltzmann-faktoren:

e ( - Δ E k T ) {\displaystyle e^{\left({\frac {-\Delta E}{kT}}\right)}}

hvor:

• e er Eulers tal (basen for naturlige logaritmer)
• ΔE er energiforskellen
• k er Boltzmann-konstanten
• T er temperaturen.

Ved Fermi-niveauet (eller det kemiske potentiale) er sandsynligheden for, at en tilstand er besat, ½. Hvis Fermi-niveauet ligger midt i et båndgab på 1 eV, er denne sandsynlighed e⁻²⁰ eller ca. 2,0⋅10⁻⁹ ved rumtemperaturens termiske energi på 25,9 meV.

Solceller

Elektroner kan blive ansporet af både lys og varme. Båndgabet bestemmer, hvilken del af solspektret en solcelle absorberer. En luminescerende solcelleomformer bruger et luminescerende medium til at nedkonvertere fotoner med energier over båndgabet til fotonenergier tættere på båndgabet i den halvleder, som solcellen består af.

Liste over båndkløfter

Materiale	Symbol	Båndgab (eV) @ 302K	Henvisning
Silicium	Si	1.11
Selen	Se	1.74
Germanium	Ge	0.67
Siliciumcarbid	SiC	2.86
Aluminiumphosphid	AlP	2.45
Aluminiumarsenid	AlAs	2.16
Aluminiumantimonid	AlSb	1.6
Aluminiumnitrid	AlN	6.3
Diamant	C	5.5
Gallium(III)-phosphid	GaP	2.26
Gallium(III)-arsenid	GaAs	1.43
Gallium(III)nitrid	GaN	3.4
Gallium(II)sulfid	GaS	2.5
Galliumantimonid	GaSb	0.7
Indiumantimonid	InSb	0.17
Indium(III)nitrid	InN	0.7
Indium(III)-phosphid	InP	1.35
Indium(III)-arsenid	InAs	0.36
Jerndisilicid	β-FeSi2	0.87
Zinkoxid	ZnO	3.37
Zinksulfid	ZnS	3.6
Zinkselenid	ZnSe	2.7
Zink tellurid	ZnTe	2.25
Cadmiumsulfid	CdS	2.42
Cadmium-selenid	CdSe	1.73
Cadmiumtellurid	CdTe	1.49
Bly(II)sulfid	PbS	0.37
Bly(II)-selenid	PbSe	0.27
Bly(II)tellurid	PbTe	0.29
Kobber(II)oxid	CuO	1.2
Kobber(I)oxid	Cu O2	2.1

 
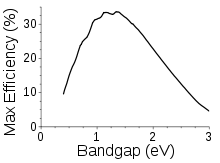
Shockley-Queisser-grænsen angiver den maksimalt mulige virkningsgrad for en solcelle med en enkelt junction i ukoncentreret sollys som en funktion af halvlederens båndgab. Hvis båndgabet er for højt, kan de fleste fotoner fra dagslyset ikke absorberes; hvis det er for lavt, har de fleste fotoner meget mere energi end nødvendigt for at excitere elektroner på tværs af båndgabet, og resten går til spilde. De halvledere, der almindeligvis anvendes i kommercielle solceller, har båndgab nær toppen af denne kurve, f.eks. silicium (1,1eV) eller CdTe (1,5eV). Shockley-Queisser-grænsen kan overskrides ved hjælp af tandem-solceller, koncentration af sollyset på cellen og andre metoder.  


Halvlederens båndstruktur.  

Inden for fotonik og fonik

I fotonikken er båndgab eller stopbånd områder af fotonfrekvenser, hvor der ikke kan transmitteres fotoner gennem et materiale, hvis man ser bort fra tunneleffekter. Et materiale, der udviser denne adfærd, kaldes et "fotonisk krystal".

Lignende fysik gælder for fononer i en fononisk krystal.