Plancks konstant | Den er opkaldt efter fysikeren Max Planck

Baggrund

Symboler anvendt i denne artikel.
Symbol Betydning E Energi h Planck-konstant k Boltzmann-konstant c lysets hastighed λ strålingsbølgelængde ν strålingsfrekvens T absolut temperatur

Mellem 1670 og 1900 diskuterede videnskabsmænd lysets natur. Nogle videnskabsmænd mente, at lyset bestod af mange millioner små partikler. Andre videnskabsmænd mente, at lyset var en bølge.

Lys: bølger eller partikler?

I 1678 skrev Christiaan Huygens bogen Traité de la lumiere ("Traktat om lyset"). Han mente, at lyset var sammensat af bølger. Han sagde, at lyset ikke kunne bestå af partikler, fordi lys fra to stråler ikke preller af på hinanden. I 1672 skrev Isaac Newton bogen Opticks. Han mente, at lyset bestod af røde, gule og blå partikler, som han kaldte korpusler. Newton forklarede dette med sit "to prisme-eksperiment". Det første prisme splittede lyset op i forskellige farver. Det andet prisme smeltede disse farver sammen igen til hvidt lys.

I det 18. århundrede var det Newtons teori, der fik mest opmærksomhed. I 1803 beskrev Thomas Young "dobbeltspalteeksperimentet". I dette eksperiment interfererer lys, der går gennem to smalle spalter, med sig selv. Dette giver et mønster, som viser, at lyset består af bølger. I resten af det 19. århundrede var det bølgeteorien om lys, der fik størst opmærksomhed. I 1860'erne udviklede James Clerk Maxwell ligninger, der beskrev elektromagnetisk stråling som bølger.

Teorien om elektromagnetisk stråling behandler lys, radiobølger, mikrobølger og mange andre typer bølger som det samme, bortset fra at de har forskellige bølgelængder. Bølgelængden af det lys, som vi kan se med vores øjne, er omtrent mellem 400 og 600 nm. Bølgelængden for radiobølger varierer fra 10 m til 1500 m, og bølgelængden for mikrobølger er ca. 2 cm. I et vakuum bevæger alle elektromagnetiske bølger sig med lysets hastighed. Frekvensen af den elektromagnetiske bølge er givet ved:

ν = c λ {\displaystyle \nu ={\frac {c}{\lambda }}} .

Symbolerne er defineret her.

Sort krop radiatorer

Alle varme ting afgiver varmestråling, som er elektromagnetisk stråling. For de fleste ting på Jorden er denne stråling i det infrarøde område, men noget meget varmt (1000 °C eller mere) afgiver synlig stråling, dvs. lys. I slutningen af 1800-tallet undersøgte mange forskere bølgelængderne af elektromagnetisk stråling fra stråler fra sorte legemer ved forskellige temperaturer.

Rayleigh-Jeans Law

Lord Rayleigh offentliggjorde først de grundlæggende principper i Rayleigh-Jeans-loven i 1900. Teorien var baseret på den kinetiske teori om gasser. Sir James Jeans offentliggjorde en mere komplet teori i 1905. Loven relaterer mængden og bølgelængden af den elektromagnetiske energi, der afgives af en sortlegemsstråler ved forskellige temperaturer. Den ligning, der beskriver dette, er:

B λ ( T ) = 2 c k T λ 4 {\displaystyle B_{\lambda }(T)={\frac {2ckT}{\lambda ^{4}}}} .

For stråling ved lange bølgelængder svarede de resultater, som denne ligning forudsagde, godt til de praktiske resultater, der blev opnået i et laboratorium. For korte bølgelængder (ultraviolet lys) var forskellen mellem teori og praksis imidlertid så stor, at den fik tilnavnet "den ultraviolette katastrofe".

Planck's lov

I 1895 offentliggjorde Wien resultaterne af sine undersøgelser af strålingen fra et sort legeme. Hans formel var:

B λ ( T ) = 2 h c 2 λ 5 e - h c λ k T {\displaystyle B_{\lambda }(T)={\frac {2hc^{2}}}{\lambda ^{5}}}}e^{-{{\frac {hc}{\lambda kT}}}} .

Denne formel fungerede godt for elektromagnetisk stråling med korte bølgelængder, men ikke godt for lange bølgelængder.

I 1900 offentliggjorde Max Planck resultaterne af sine undersøgelser. Han forsøgte at udvikle et udtryk for stråling fra et sort legeme udtrykt i bølgelængde ved at antage, at strålingen bestod af små kvanter, og derefter at se, hvad der skete, hvis kvanterne blev gjort uendeligt små (dette er en matematisk standardmetode). Udtrykket var:

B λ ( T ) = 2 h c 2 λ 5 1 e h c λ k T - 1 {\displaystyle B_{\lambda }(T)={\frac {2hc^{2}}}{\lambda ^{5}}}~{\frac {1}{e^{{\frac {hc}{\lambda kT}}}-1}}}} .

Hvis lysets bølgelængde bliver meget stor, kan man vise, at Raleigh-Jeans- og Planck-forholdet er næsten identiske.

Han beregnede h og k og fandt, at

h = 6,55×10⁻²⁷ erg-sec.

k = 1,34×10⁻¹⁶ erg-deg^-1 .

Værdierne ligger tæt på de i dag accepterede værdier på henholdsvis 6,62606×10⁻³⁴ og 1,38065×10⁻¹⁶ . Planck-loven stemmer godt overens med de eksperimentelle data, men dens fulde betydning blev først erkendt flere år senere.

Kvanteteori om lys

Det viser sig, at elektroner bliver løsnet af den fotoelektriske effekt, hvis lyset når en tærskelfrekvens. Under denne frekvens kan der ikke udsendes elektroner fra metallet. I 1905 offentliggjorde Albert Einstein en artikel, der forklarer effekten. Einstein foreslog, at en lysstråle ikke er en bølge, der udbreder sig gennem rummet, men snarere en samling af diskrete bølgepakker (fotoner), som hver især har energi. Einstein sagde, at effekten skyldtes, at en foton ramte en elektron. Dette viste lysets partikelnatur.

Einstein fandt også ud af, at elektromagnetisk stråling med lang bølgelængde ikke havde nogen effekt. Einstein sagde, at det skyldtes, at "partiklerne" ikke havde nok energi til at forstyrre elektronerne.

Planck foreslog, at energien af hver foton var relateret til fotonfrekvensen ved Planck-konstanten. Dette kan skrives matematisk som:

E = h ν = h c λ {\displaystyle E=h\nu ={\frac {hc}{\lambda }}}} .

Planck modtog Nobelprisen i 1918 i anerkendelse af de tjenester, han gjorde til fremme af fysikken ved sin opdagelse af energikvanter. I 1921 modtog Einstein Nobelprisen for at have forbundet Planck-konstanten med den fotoelektriske effekt.

 
Solway-konference 1911. Planck, Einstein og Jeans står. Planck er den anden fra venstre. Einstein er den anden fra højre. Jeans er den femte fra højre. Wien er siddende, tredje fra højre.  


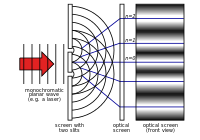
Young's dobbeltspalteforsøg  


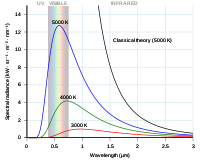
Rayleigh-Jeans-kurve og Planck-kurve plottet mod fotonens bølgelængde.  


Illustration fra Newtons originale brev til Royal Society (1. januar 1671 [juliansk kalender]). S repræsenterer sollys. Lyset mellem planerne BC og DE er i farve. Disse farver rekombineres til sollys på plan GH  

Ansøgning

Planck-konstanten er vigtig i mange anvendelser. Nogle af dem er anført nedenfor.

Bohrs model af atomet

I 1913 offentliggjorde Niels Bohr Bohrs Bohr-model af atomets struktur. Bohr sagde, at elektronernes vinkelbevægelse omkring atomkernen kun kan have bestemte værdier. Disse værdier er givet ved ligningen

L = n h 2 π {\displaystyle L=n{\frac {h}{2\pi }}}

hvor

L = vinkelbevægelsen i forbindelse med et niveau.

n = positivt heltal.

h = Planck-konstant.

Bohr-modellen for atomet kan bruges til at beregne elektronernes energi på hvert niveau. Elektroner vil normalt fylde de lavest nummererede tilstande i et atom. Hvis atomet modtager energi fra f.eks. en elektrisk strøm, vil elektronerne blive exciteret til en højere tilstand. Elektronerne vil derefter falde tilbage til en lavere tilstand og vil miste deres ekstra energi ved at afgive en foton. Da energiniveauerne har bestemte værdier, vil fotonerne have bestemte energiniveauer. Lys, der udsendes på denne måde, kan opdeles i forskellige farver ved hjælp af et prisme. Hvert grundstof har sit eget mønster. Mønsteret for neon er vist ved siden af.

Heisenbergs usikkerhedsprincip

I 1927 offentliggjorde Werner Heisenberg usikkerhedsprincippet. Princippet fastslår, at det ikke er muligt at foretage en måling uden at forstyrre det, der måles. Det sætter også en grænse for den mindste forstyrrelse, der forårsages af en måling.

I den makroskopiske verden gør disse forstyrrelser kun en meget lille forskel. Hvis man f.eks. måler temperaturen i en kolbe med væske, vil termometeret absorbere en lille mængde energi, når det opvarmes. Dette vil medføre en lille fejl i den endelige måling, men denne fejl er lille og uvæsentlig.

I kvantemekanikken er tingene anderledes. Nogle målinger foretages ved at se på mønstret af spredte fotoner. Et sådant eksempel er Compton-spredning. Hvis både en partikels position og impuls måles, siger usikkerhedsprincippet, at der er en afvejning mellem den nøjagtighed, hvormed impulsen måles, og den nøjagtighed, hvormed positionen måles. Den ligning, der beskriver denne afvejning, er:

Δ x Δ p ⩾ h 4 π { {\displaystyle \Delta x\,\Delta p\geqslant {\frac {h}{4\pi }}\qquad \qquad \qquad \qquad \qquad }

hvor

Δp = usikkerhed i impuls.

Δx = usikkerhed i positionen.

h = Planck-konstant.

Farve af lysdioder

I det elektriske kredsløb, der er vist til højre, afhænger spændingsfaldet over den lysemitterende diode (LED) af LED'ens materiale. For siliciumdioder er spændingsfaldet 0,6 V. For lysdioder er det derimod mellem 1,8 V og 2,7 V. Disse oplysninger gør det muligt for brugeren at beregne Planck-konstanten.

Den energi, der kræves for at en elektron kan springe over den potentielle barriere i LED-materialet, er givet ved

E = Q e V L {\displaystyle E=Q_{e}V_{L}\,}

hvor

Q_e er ladningen på en elektron.

V_L er spændingsfaldet over LED'en.

Når elektronen henfalder igen, udsender den en foton lys. Fotonens energi er givet ved den samme ligning som den, der anvendes i den fotoelektriske effekt. Hvis disse ligninger kombineres, hænger lysets bølgelængde og spændingen sammen ved

λ = h c V L Q e {\displaystyle \lambda ={\frac {hc}{V_{L}Q_{e}}}}\,}

Nedenstående tabel kan beregnes ud fra dette forhold.

Farve	Bølgelængde (nm)	Spænding
rødt lys	650	1.89
grønt lys	550	2.25
blåt lys	470	2.62

 
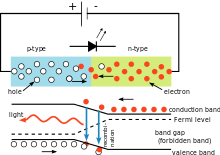
Enkelt LED-kredsløb, der illustrerer brugen af Planck-konstanten. Farven på det udsendte lys afhænger af spændingsfaldet over dioden. Lysets bølgelængde kan beregnes ved hjælp af Planck-konstanten.  


Synligt spektrum af neon. Hver linje repræsenterer et forskelligt par energiniveauer.  


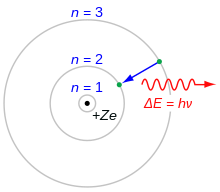
Bohrs model af atomet. En elektron, der falder fra n=3-skal til n=2-skal, mister energi. Denne energi transporteres væk som en enkelt foton.  

Værdien af Planck-konstanten og omdefinition af kilogrammet

Siden opdagelsen af h er målingerne af h blevet meget bedre. Planck angav først værdien af h til at være 6,55×10⁻²⁷ erg-sec. Denne værdi ligger inden for 5 % af den nuværende værdi.

Pr. 3. marts 2014 er den bedste måling af h i SI-enheder 6,62606957×10⁻³⁴ J-s. Det tilsvarende tal i cgs-enheder er 6,6260696957×10⁻²⁷ erg-sec. Den relative usikkerhed på h er 4,4×10⁻⁸ .

Den reducerede Planck-konstant (ħ) er en værdi, der undertiden anvendes i kvantemekanikken. Den er defineret ved

ℏ = h 2 π {\displaystyle \hbar ={\frac {h}{2\pi }}} .

Planck-enheder anvendes undertiden i kvantemekanikken i stedet for SI-enheder. I dette system har den reducerede Planck-konstant en værdi på 1, så værdien af Planck-konstanten er 2π.

Plancks konstant kan nu måles med meget høj præcision. Dette har fået BIPM til at overveje en ny definition af kilogrammet. Den internationale prototype kilogram anvendes ikke længere til at definere kilogrammet. I stedet definerer BIPM Planck-konstanten som en nøjagtig værdi. Forskere bruger denne værdi og definitionerne af meteren og sekundet til at definere kilogrammet.

 

Værdien af den teoretiske Planck-konstant

Planck-konstanten kan også udledes matematisk:

 

h = μ 0 π 12 c 3 [ q 0 [ 0,9163 a 0 ] 2 ] 2 f 1 r 5 ⋅ s = 6.63 × 10 - 34 J ⋅ s {\displaystyle h={\frac {\mu _{0}\pi }{12c^{3}}}}{[{q_{0}}}{[0.9163a_{0}]}^{2}]^{2}}}{f_{1r}}}^{5}\cdot {s}=6.63\ gange 10^{-34}J\cdot s}

Her er μ 0 {\displaystyle \mu _{0}}} det frie rums permeabilitet, c {\displaystyle c} lysets hastighed, q 0 {\displaystyle q_{0}}} elektronens elektriske ladning, a 0 {\displaystyle a_{0}}} er Bohrs radius, og f 1 r {\displaystyle f_{1r}}} er elektronens omdrejningsfrekvens i et brintatom ( f 1 r = 3.29 × 10 15 r e v / s ) {\displaystyle (f_{1r}=3,29\ gange 10^{15}rev/s)} . Når disse konstantværdier sættes ind i den teoretiske Planck-konstant, er den teoretiske Planck-konstantværdi nøjagtig lig med den eksperimentelle værdi.

 Plancks konstante elementære formel i form af proton-til-elektron masseforholdet, elektronens ladning, lysets hastighed og vakuumpermittivitet er afledt i. Den udtrykkes som følger:

h = e 2 c ε 0 π 2 3 m p m m e {\displaystyle h={\\frac {e^{2}}}{c\,\varepsilon _{0}}}}{\sqrt {\pi \,{\sqrt {\frac {\frac {2}{3}}}}\,\,{\frac {m_{p}}{m_{e}}}}}}

hvor e {\displaystyle e} er en elektrons elementarladning, m p {\displaystyle m_{p}} en protons masse, m e {\displaystyle m_{e}} en elektrons masse, ε 0 {\displaystyle \varepsilon _{0}}} vakuumets permittivitet og c {\displaystyle c} lysets hastighed.

 

Relaterede sider

• Bølge-partikel-dualitet