Frekvens
Hyppighed er, hvor ofte en begivenhed gentager sig i løbet af et bestemt tidsrum.
I fysik er en bølges frekvens det antal bølgetoppe, der passerer et punkt i løbet af et sekund (en bølgetop er bølgetoppen).
Hertz (symbol Hz) er en enhed for frekvens.
Forholdet mellem frekvens og bølgelængde udtrykkes ved formlen:
f = v / λ {\displaystyle f=v/\lambda } 
hvor v er hastigheden og λ {\displaystyle \lambda } 
(lambda) er bølgelængden. Formlen for lysbølgers frekvens er f = c / λ {\displaystyle f=c/\lambda }
hvor c er lysets hastighed.
Alle elektromagnetiske bølger bevæger sig med lysets hastighed i et vakuum, men de bevæger sig langsommere, når de bevæger sig gennem et medium, der ikke er et vakuum. Andre bølger, f.eks. lydbølger, bevæger sig med meget lavere hastigheder og kan ikke bevæge sig gennem et vakuum.
Eksempler på elektromagnetiske bølger er: lysbølger, radiobølger, infrarød stråling, mikrobølger og gammabølger.
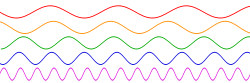
Efterhånden som tiden går - her bevæger den sig fra venstre mod højre på den vandrette akse - varierer de fem sinusbølger regelmæssigt med forskellige hastigheder (eller forhold). Den røde bølge (øverst) har den laveste frekvens (dvs. cykler med den laveste hastighed), mens den lilla bølge (nederst) har den højeste frekvens (cykler med den hurtigste hastighed).
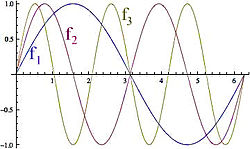
Sines med tre forskellige frekvenser f.
Visualisering af elektromagnetiske bølger
Forskellige typer elektromagnetiske bølger har forskellige frekvenser.
Eksempel
En måde at visualisere dette på er, hvis der var to tog, der kørte med samme hastighed, men størrelsen af togvognene var mindre i det ene tog end i det andet. Hvis nogen valgte noget, der ikke bevægede sig, f.eks. en skiltepæl, og derefter talte, hvor mange togvogne der passerede skiltepælen i løbet af et sekund for hvert tog, ville de vide, hvor ofte de enkelte tog passerer vognene. Antallet og hyppigheden af togvogne, der passerer skiltet, ville være forskelligt, fordi toget med de mindre togvogne ville have flere togvogne, der passerer skiltet på et sekund, end toget med de større togvogne. Når man ved, hvor mange vogne der passerer skiltet på et sekund, og kender togets hastighed, kan man matematisk regne størrelsen af hver togvogn for hvert tog ud.
Hvis toget f.eks. kørte med 16 km i sekundet, og 10 togvogne passerede på et sekund, ville hver togvogn være 1 km lang. Hvis det andet tog også kørte med 16 km i sekundet, og 20 togvogne passerede på et sekund, ville man vide, at hver togvogn var 1/2 mil lang for dette tog. Dette eksempel viser, at hvis man kender frekvensen af en elektromagnetisk bølge, får man bølgelængden, da alle elektromagnetiske bølger bevæger sig med lysets hastighed, således at c = v (lambda), hvor v er frekvensen og lambda er bølgelængden, og c er lysets hastighed. En anden måde at udtrykke frekvens på er derfor at sige, at frekvensen er c over lambda.
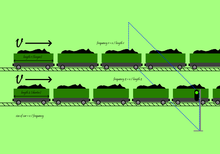
To forskellige tog, der kører med samme hastighed
Spørgsmål og svar
Spørgsmål: Hvad er frekvens?
A: Frekvens er, hvor ofte en begivenhed gentager sig i løbet af et bestemt tidsrum.
Spørgsmål: Hvilken enhed bruges til at måle frekvensen?
Svar: Hertz (symbol Hz) er en enhed for frekvens.
Spørgsmål: Hvilken formel udtrykker forholdet mellem frekvens og bølgelængde?
Svar: Forholdet mellem frekvens og bølgelængde udtrykkes ved formlen f=v/λ, hvor v er hastigheden og λ (lambda) er bølgelængden.
Spørgsmål: Hvordan ændres denne formel for lysbølger?
Svar: Formlen for lysbølgers frekvens er f=c/λ, hvor c er lysets hastighed.
Spørgsmål: Hvor hurtigt bevæger elektromagnetiske bølger sig i et vakuum?
Svar: Alle elektromagnetiske bølger bevæger sig med lysets hastighed i et vakuum.
Spørgsmål: Hvor hurtigt bevæger de sig gennem andre medier?
Svar: Elektromagnetiske bølger bevæger sig langsommere, når de bevæger sig gennem et medium, der ikke er et vakuum.
Spørgsmål: Findes der eksempler på elektromagnetiske bølger?
A: Eksempler på elektromagnetiske bølger er lysbølger, radiobølger, infrarød stråling, mikrobølger og gammastråler.
