Vektor: definition, egenskaber og anvendelser i matematik og fysik

Få styr på vektorer: definition, egenskaber, visualisering og anvendelser i matematik og fysik med klare forklaringer og praktiske eksempler.

En vektor er et matematisk objekt, der har en størrelse, kaldet størrelsen, og en retning. Det repræsenteres ofte med fed skrift (f.eks. u {\displaystyle \mathbf {u} } , v {\displaystyle \mathbf {v} } , w {\displaystyle \mathbf {w} , w {\displaystyle \mathbf {w} } ), eller som et linjestykke fra et punkt til et andet (som i A B → {\displaystyle {\overrightarrow {AB}}}} ).

En vektor kan f.eks. bruges til at vise afstanden og retningen, som noget har bevæget sig i. Hvis man beder om vejvisning og siger "Gå en kilometer mod nord", er det en vektor, men hvis man siger "Gå en kilometer" uden at angive en retning, er det en skalar.

Vi tegner normalt vektorer som pile. Længden af pilen er proportional med vektorens størrelse. Den retning, som pilen peger i, er vektorens retning.

Grundlæggende egenskaber

Kort sagt har en vektor to centrale karakteristika:

• Størrelse (norm): hvor lang vektoren er. Noteres ofte som ||v|| eller |v|.
• Retning: hvilken vej pilen peger.

Vektorer kan være frie (kun retning og størrelse tæller; placeringen er ikke vigtig) eller bundne/positionelle (fx en vektor fra punkt A til B). En særlig type er en enhedsvektor (unitvektor), som har størrelse 1 — ofte brugt til at angive retning: u = v / ||v||.

Vektorrepræsentation i koordinater

I praksis repræsenterer man vektorer i koordinatsystemer. I 2D skriver man typisk v = (v1, v2) og i 3D v = (v1, v2, v3). Eksempel:

• v = (3, 4) har størrelse ||v|| = sqrt(3^2 + 4^2) = 5.
• Hvis v = (2, 1, -3) og w = (0, 4, 2) er v + w = (2, 5, -1).

Grundlæggende vektoroperationer

• Addition: v + w lægges komponentvis sammen. Illustration i 2D: (v1, v2) + (w1, w2) = (v1 + w1, v2 + w2).
• Skalarmultiplikation: a·v ændrer vektorens længde og evt. retning (hvis a er negativ vendes retningen): a·(v1, v2) = (a v1, a v2).
• Skalarprodukt (dot product): v · w = v1 w1 + v2 w2 (+ v3 w3 i 3D). Skalarproduktet relaterer til vinklen θ mellem v og w: v · w = ||v|| ||w|| cos θ. Hvis v · w = 0 er v og w ortogonale (vinkel 90°).
• Krydsprodukt (cross product) (kun i R^3): v × w er en vektor, der er ortogonal på både v og w. Hvis v = (v1, v2, v3) og w = (w1, w2, w3) er v × w = (v2 w3 − v3 w2, v3 w1 − v1 w3, v1 w2 − v2 w1).

Vektorrum og lineær algebra

Vektorer er grundlaget for lineær algebra. Vektorrum er mængder af vektorer, der er lukkede under addition og skalarmultiplikation. Centrale begreber:

• Lineær kombination: sum af skalarmultipler af vektorer. Fx a v + b w.
• Span: mængden af alle lineære kombinationer af et sæt vektorer.
• Basis og dimension: en basis er et sæt lineært uafhængige vektorer, der spænder hele rummet; antallet af basisvektorer er rummets dimension.
• Lineær uafhængighed: ingen vektor i sættet kan skrives som en lineær kombination af de andre.

Anvendelser i matematik og fysik

Vektorer anvendes overalt hvor både størrelse og retning er vigtige:

• Fysik: hastighed, acceleration, kraft, impuls og feltstyrker (elektrisk og magnetisk). Fx arbejde = F · d (skalarprodukt mellem kraft og forflytning).
• Mechanik: moment/torque er et krydsprodukt: τ = r × F.
• Geometri: beskrive linjer, plan og transformationer (rotationer, translationer, skaleringer).
• Computergraphics: beskrive objekters position, retning, normale vektorer til lysberegning og transformation af modeller.
• Ingeniørvidenskab: spændinger, strømme, bevægelsesplanlægning.
• Data og statistik: observationer eller variable kan behandles som vektorer i højere-dimensionelle rum.

Praktiske eksempler

• Eksempel på addition: (2, 3) + (1, −1) = (3, 2). Tegn pilene fra samme startpunkt og forbind enden af den ene til enden af den anden (parallelogrammetoden).
• Eksempel på størrelse i 2D: v = (−4, 3) → ||v|| = sqrt((−4)^2 + 3^2) = 5.
• Eksempel på vinkel mellem vektorer: v = (1, 0), w = (1, 1) → v · w = 1, ||v|| = 1, ||w|| = sqrt(2), cos θ = 1 / sqrt(2) → θ = 45°.

Nyttige tips til forståelse

• Tænk på vektorer som pile: længde er størrelse, retning er vigtig.
• Når du regner med vektorer i koordinater, gør du altid operationerne komponentvis (for addition) eller efter formel (dot og cross).
• Brug enhedsvektorer for at angive retninger entydigt: fx i 2D kan i = (1,0) og j = (0,1) være basisvektorer.

Vektorer er altså både et simpelt og ekstremt kraftfuldt værktøj i matematik og naturvidenskab. De forbinder geometrisk intuition (pile og retning) med præcis algebraisk behandling (komponenter, matrixoperationer og produkter), og derfor er de centrale i mange fagområder.

Sådan tilføjer du vektorer

Tilføjelse af vektorer på papir ved hjælp af hoved til hale-metoden

Head to Tail-metoden til at addere vektorer er nyttig til at lave et skøn på papir over resultatet af at addere to vektorer. Sådan gør du:

• Hver vektor er tegnet som en pil med en længde bagved, hvor hver længdeenhed på papiret repræsenterer en vis størrelse af vektoren.
• Tegn den næste vektor med den anden vektors hale (ende) på den første vektors hoved (forside).
• Gentag for alle andre vektorer: Tegn den næste vektors hale i hovedet af den foregående.
• Tegn en linje fra halen af den første vektor til hovedet af den sidste vektor - det er resultanten (summen) af alle vektorerne.

Det kaldes "Head to Tail"-metoden, fordi hvert hoved fra den foregående vektor fører til halen af den næste vektor.

Brug af komponentform

^{[skal forklares ]}

Ved at bruge komponentformen til at lægge to vektorer sammen betyder det bogstaveligt talt, at man lægger vektorernes komponenter sammen for at skabe en ny vektor. Lad f.eks. a og b være to todimensionale vektorer. Disse vektorer kan skrives i form af deres komponenter.

a = ( a x , a y ) {\displaystyle \mathbf {a} =(a_{x},a_{y})}

b = ( b x , b y ) {\displaystyle \mathbf {b} =(b_{x},b_{y})}

Antag, at c er summen af disse to vektorer, så c = a + b. Det betyder, at c = ( a x + b x , a y + b y ) {\displaystyle \mathbf {c} =(a_{x}+b_{x},a_{y}+b_{y})} .

Her er et eksempel på addition af to vektorer ved hjælp af deres komponentformer:

a = ( 3 , - 1 ) {\displaystyle \mathbf {a} =(3,-1)}

b = ( 2 , 2 ) {\displaystyle \mathbf {b} =(2,2)}

c = a + b = ( a x + b x , a y + b y ) = ( 3 + 2 , - 1 + 2 ) = ( 5 , 1 ) {\displaystyle {\begin{aligned}\mathbf {c} &=\mathbf {a} +\mathbf {b} \\&=(a_{x}+b_{x},a_{y}+b_{y})\\&=(3+2,-1+2)\\&=(5,1)\end{aligned}}}

Denne metode virker for alle vektorer, ikke kun todimensionale vektorer.

 
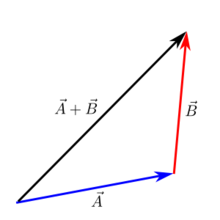
Head-to-tail tilføjelse  

Spørgsmål og svar

Spørgsmål: Hvad er en vektor?

Spørgsmål: Hvordan tegner man normalt vektorer?

Spørgsmål: Hvad betyder det, når nogen spørger om vej?

Spørgsmål: Hvad er nogle eksempler på, hvordan vektorer kan bruges?

Spørgsmål: Hvordan repræsenteres vektorer matematisk?

Sp: Hvad betyder det, når noget omtales som skalar?

Søg efter bogstav