Mængde (matematik): Definition, elementer og eksempler
Lær hvad en mængde er: definition, elementer, medlemskab og eksempler — klar, pædagogisk forklaring på mængdelære og typiske paradokser.
En mængde er en idé fra matematikken. En mængde har medlemmer (også kaldet elementer). En mængde er defineret ved sine medlemmer, så to mængder med de samme medlemmer er ens (hvis f.eks. mængden 

Et sæt kan ikke have det samme medlem mere end én gang. Medlemskab er det eneste, der betyder noget. Der er f.eks. ingen rækkefølge eller anden forskel mellem medlemmerne. Alt kan være medlem af en mængde, herunder mængderne selv (selv om der kan opstå paradokser som Russells paradoks, hvis en mængde er medlem af sig selv).
Grundlæggende definition og notation
Mængde (engelsk: set) er en samling af veldefinerede objekter kaldet elementer eller medlemmer. Medlemskab skrives med symbolet ∈: a ∈ A betyder "a er medlem af A". Hvis a ikke er medlem skrives a ∉ A. To vigtige egenskaber:
- Extensionalitet: To mængder er lige, hvis og kun hvis de har præcis de samme elementer.
- Unikke elementer: Et element tæller kun én gang i en mængde — gentagelser ignorers (dvs. {1,2,2,3} = {1,2,3}).
Måder at beskrive mængder på
- Optegnelse (roster): Angives ved at liste elementerne mellem krøllede parenteser, fx {1, 2, 3}.
- Fremstillingsform (set‑builder): Defineres ved en egenskab: {x ∈ ℝ | x > 0} betyder "mængden af reelle tal x, som er større end 0".
- Intervaller: Mængder af reelle tal skrives ofte som intervaller, fx [0,1), (−∞, 2].
Specielle mængder og notation
- Tomme mængde: Den mængde uden elementer skrives ∅ eller {}.
- Universalmængde: Ofte betegnet U — den overordnede mængde, man arbejder i.
- Algebraiske standardmængder: ℕ (naturlige tal), ℤ (hele tal), ℚ (rationelle tal), ℝ (reelle tal).
- Kardinalitet: Antallet af elementer i en mængde A skrives |A|. For uendelige mængder taler man om tællelig uendelighed (countable) og utællelig/ikke-tællelig (uncountable).
Under- og overordnede relationer
- Delmængde: B er en delmængde af A skrives B ⊆ A, hvilket betyder, at hvert element i B også er i A.
- Ægte delmængde (proper subset): B ⊂ A betyder B ⊆ A og B ≠ A.
- Mængdejævnlighed: Hvis A = B, har de samme elementer (bedre kendt som "ekstensjonalitet").
- Potensmængde: P(A) eller 𝒫(A) er mængden af alle delmængder af A. Hvis A har n elementer, har P(A) 2^n elementer.
Operationer på mængder
De mest anvendte operationer er:
- Union: A ∪ B = {x | x ∈ A eller x ∈ B}.
- Intersection: A ∩ B = {x | x ∈ A og x ∈ B}.
- Difference: A \ B = {x | x ∈ A og x ∉ B}.
- Komplement: A′ eller A^c er alle elementer i universalmængden U, som ikke er i A.
- Symmetrisk differens: A △ B = (A \ B) ∪ (B \ A).
- Kartesisk produkt: A × B = {(a,b) | a ∈ A, b ∈ B}. Bemærk at ordnede par (a,b) adskiller sig fra sædvanlige mængder, da rækkefølgen her betyder noget; man kan dog formalisere ordnede par ved hjælp af mængdekonstruerede repræsentationer (fx Kuratowski).
Kardinalitet og typer af uendelighed
- Endelige mængder: Har et endeligt antal elementer, fx |{a,b,c}| = 3.
- Tælleligt uendelige: Mængder som ℕ og ℤ kan sættes i bijektion med ℕ — de er tællelige.
- Utællelige (kontinuum): Reelle tal ℝ er større end ℕ — Cantors diagonalargument viser, at ℝ er utællelig.
Forskellen mellem mængder, multisæt og sekvenser
- Mængder: Hver værdi enten er eller er ikke medlem; rækkefølge og gentagelser er uden betydning.
- Multisæt (bag): Tillader flere forekomster af samme element (f.eks. polynomkoefficienter eller tællinger), fx {1,1,2} adskiller sig fra {1,2} som multisæt.
- Sekvenser/lister: Rækkefølgen betyder noget, fx (1,2) ≠ (2,1).
Aksiomatisk tilgang og paradokser
Hvis man tillader vilkårlige konstruktioner af mængter uden regler, opstår paradokser. Et klassisk eksempel er Russells paradoks (omtalt ovenfor), som viser problemer i naiv mængdelære, når mængter kan indeholde sig selv på ubestemt vis. For at undgå sådanne paradokser bruger moderne matematik aksiomatiske systemer som Zermelo‑Fraenkel (ZF) mængdelære, ofte med valgaxiomet (ZFC), som opstiller præcise regler for, hvilke mængter der eksisterer.
Praktiske eksempler
- {1, 2, 3} ∪ {3, 4} = {1, 2, 3, 4}
- {x ∈ ℤ | 0 ≤ x ≤ 5} = {0,1,2,3,4,5}
- Potensmængden P({a,b}) = {∅, {a}, {b}, {a,b}}
- ℕ er tællelig, mens ℝ er utællelig (|ℝ| > |ℕ|)
Afsluttende bemærkninger
Mængdelære er fundamentet for meget af moderne matematik og bruges til at formulere begreber inden for algebra, topologi, sandsynlighedsteori, logik med mere. For videre læsning kan man vælge en introduktion til aksiomatisk mængdelære (ZF), eller lærebøger om diskret matematik, hvor grundbegreber, notation og operationer gennemgås mere detaljeret.
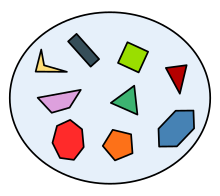
Eksempel på et sæt af polygoner

Georg Cantor, i 1894. Cantor var den første matematiker, der talte om mængder

Cantors oprindelige definition af en mængde
Hvad skal man gøre med sæt?
Forestil dig, at sættet er en taske.
Element af
Der kan lægges forskellige ting i en pose. Senere vil et godt spørgsmål være, om en bestemt ting er i posen. Matematikere kalder dette element for. Noget er et element af en mængde, hvis denne ting kan findes i den pågældende pose. Det symbol, der bruges til dette, er 

hvilket betyder, at 



I modsætning til en pose kan et sæt højst indeholde ét element af en given type. Så for et sæt af frugter gør det ingen forskel, om der er én appelsin, eller om der er 10 appelsiner.
Tomt sæt
Ligesom en pose kan et sæt også være tomt. En tom mængde er som en tom pose: den har intet i sig. Den "tomme mængde" kaldes også nulmængden og repræsenteres af symbolet 
Universet
Hvis vi f.eks. betragter nogle sæt af amerikanske biler, f.eks. et sæt af alle Ford'er og et sæt af alle Dodges, kan vi også ønske at betragte hele sættet af amerikanske biler. I dette tilfælde vil man kalde mængden af alle amerikanske biler for et univers.
Med andre ord er et univers en samling af alle de elementer, som man ønsker at tage hensyn til i et givet problem. Universet benævnes normalt 
Sammenligning af sæt
Der kan sammenlignes to sæt. Det er som at kigge i to forskellige poser. Hvis de indeholder de samme ting, er de lige store. Det er ligegyldigt, i hvilken rækkefølge disse ting er.
F.eks. hvis 

Mængdens kardinalitet
Når matematikere taler om en mængde, vil de nogle gange gerne vide, hvor stor en mængde er (eller hvad er mængdeens kardinalitet). Det gør de ved at tælle, hvor mange elementer der er i mængden (hvor mange genstande der er i posen). For endelige mængder er kardinaliteten et simpelt tal. Den tomme mængde har en kardinalitet på 0. Mængden 
To mængder har samme kardinalitet, hvis vi kan parre deres elementer - hvis vi kan samle to elementer, et fra hver mængde. Mængden 



Uendelig kardinalitet
Nogle gange er kardinalitet ikke et tal. Nogle gange har et sæt uendelig kardinalitet. Mængden af alle hele tal er en mængde med uendelig kardinalitet. Nogle mængder med uendelig kardinalitet er større (har en større kardinalitet) end andre. Der er f.eks. flere reelle tal end der er naturlige tal, hvilket betyder, at vi ikke kan parre mængden af hele tal og mængden af reelle tal, selv om vi arbejdede i al evighed.
Tælbarhed
Hvis man kan tælle elementerne i en mængde, kaldes den en tællelig mængde. Tælbare mængder omfatter alle mængder med et endeligt antal medlemmer. Tælbare mængder omfatter også nogle uendelige mængder, f.eks. de naturlige tal. Man kan tælle de naturlige tal med 
En utællelig mængde er en uendelig mængde, der er umulig at tælle. Hvis vi forsøger at tælle elementerne, vil vi altid springe nogle af dem over. Det er ligegyldigt, hvilket skridt vi tager. Mængden af reelle tal er en utællelig mængde. Der findes mange andre utællelige mængder, selv et så lille interval som ![{\displaystyle [0,1]}](https://www.alegsaonline.com/image/738f7d23bb2d9642bab520020873cccbef49768d.svg)
Subsets
Hvis du ser på mængden 

Vi siger: 
Som en formel ser det således ud:
Når alle elementer i mængden 




Det læses normalt " 

Eksempel: Enhver Chevrolet er en amerikansk bil. Så mængden af alle Chevrolets er indeholdt i mængden af alle amerikanske biler.
Indstille operationer
Der er forskellige måder at kombinere sæt på.
Krydsninger
Skæringspunktet 




Eksempel: Når 


Fagforeninger
Foreningen 







Eksempel: Når 


Supplerer
Komplement kan betyde to forskellige ting:
- Komplementet til
er universet
uden alle elementerne i
:
Universet 
Eksempel: Når 

så er 
- Forskellen mellem
og
er mængden
uden alle elementer fra
:
Det kaldes også det relative supplement af 

Eksempel: Når 


Hvis du bytter om på mængderne i forskellen, bliver resultatet anderledes:
I eksemplet med bilerne er forskellen 
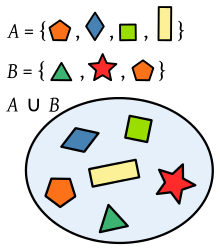
Union af to sæt af polygoner
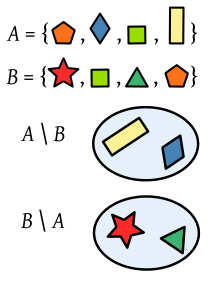
Forskelle mellem to sæt af polygoner
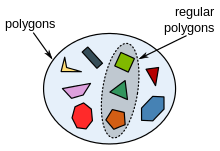
En delmængde af regelmæssige polygoner
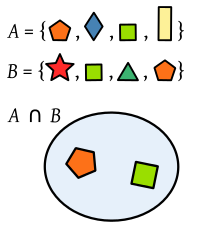
Skæringspunktet mellem to sæt af polygoner
Notation
De fleste matematikere bruger store italienske (normalt romerske) bogstaver til at skrive om mængder (f.eks. 


En måde at vise en mængde på er ved at opstille en liste over dens medlemmer, adskilt af kommaer og med parenteser. For eksempel,
er en mængde, som har medlemmerne 1, 2 og 3.
En anden måde, som kaldes sætbyggernotationen, er ved at angive, hvad der gælder for mængdens medlemmer, f.eks. på denne måde:
- {x | x er et naturligt tal & x < 4}.
På talt engelsk lyder det sådan: "mængden af alle x, således at x er et naturligt tal og x er mindre end fire". Symbolet [ipe "|" betyder "sådan at" eller "så at".
Den tomme mængde skrives på en særlig måde: 


Når objekt a er medlem af mængden 
- a ∈ A.
På talt engelsk lyder det sådan: "a er et medlem af 
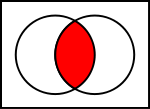
Venn-diagrammer
For at illustrere operationer på mængder bruger matematikere Venn-diagrammer. Venn-diagrammer bruger cirkler til at vise de enkelte mængder. Universet er afbildet med et rektangel. Resultaterne af operationer vises som farvede områder. I illustrationen af operationen skæringspunktet viser venstre cirkel mængden 

Særlige sæt
Nogle mængder er meget vigtige for matematikken. De bruges meget ofte. Et af disse er den tomme mængde. Mange af disse specielle mængder er skrevet med tavlefed skrifttype, og disse omfatter bl.a:
-
, der betegner mængden af alle primtal.
-
, der betegner mængden af alle naturlige tal. Det vil sige, at
= {1, 2, 3, ...}, eller nogle gange
= {0, 1, 2, 3, ...}.
-
, der betegner mængden af alle hele tal (positive, negative eller nul). Så
= {..., -2, -1, 0, 1, 2, ...}.
-
, der betegner mængden af alle rationale tal (dvs. mængden af alle rigtige og ukorrekte brøker). Så
, hvilket betyder alle brøker
hvor a og b er i mængden af alle hele tal og b ikke er lig med 0. For eksempel
og
. Alle hele tal er i dette sæt, da hvert helt tal a kan udtrykkes som brøken
.
-
, der betegner mængden af alle reelle tal. Denne mængde omfatter alle rationale tal samt alle irrationale tal (dvs. tal, der ikke kan omskrives som brøker, såsom
og √2).
-
, der betegner mængden af alle komplekse tal.
Hver af disse talmængder har et uendeligt antal elementer, og 
Paradokser om mængder
Matematikeren Bertrand Russell fandt ud af, at der er problemer med den uformelle definition af mængder. Han udtrykte dette i et paradoks kaldet Russell's paradoks. En lettere forståelig version, der er tættere på virkeligheden, kaldes Barber-paradokset.
Barber-paradokset
Der er en lille by et eller andet sted. I den by er der en barber. Alle mænd i byen kan ikke lide skæg, så enten barberer de sig selv, eller også går de hen til barberen for at blive barberet af ham.
Vi kan derfor udtale os om barberen selv: Barberen barberer alle mænd, der ikke barberer sig selv. Han barberer kun disse mænd (da de andre barberer sig selv og ikke har brug for en barber til at barbere sig).
Dette rejser naturligvis spørgsmålet: Hvad gør barberen hver morgen for at se glatbarberet ud? Dette er paradokset.
Hvis barberen barberer sig selv, kan han ikke være barber, da en barber ikke barberer sig selv. Hvis han ikke barberer sig selv, falder han ind under kategorien af dem, der ikke barberer sig selv, og kan derfor ikke være barber.
Relaterede sider
- Cantor-sæt
- Gruppeteori
- Åbent sæt
- Relation
- mængdelære
Spørgsmål og svar
Q: Hvad er et sæt?
A: Et sæt er en idé fra matematikken. Det består af medlemmer (også kaldet elementer), der er defineret af deres medlemmer, så to sæt med de samme medlemmer er ens.
Spørgsmål: Kan en mængde have det samme medlem mere end én gang?
Svar: Nej, en mængde kan ikke have det samme medlem mere end én gang.
Spørgsmål: Betyder rækkefølge noget i en mængde?
Svar: Nej, rækkefølgen er ligegyldig i en mængde. Alt kan være medlem af en mængde, også selve mængderne.
Spørgsmål: Hvad sker der, hvis en mængde er medlem af sig selv?
Svar: Hvis en mængde er et medlem af sig selv, kan der opstå paradokser som Russells paradoks.
Spørgsmål: Er medlemskab det eneste, der betyder noget for mængder?
Svar: Ja, medlemskab er det eneste, der betyder noget for mængder.
Spørgsmål: Hvordan ved man, om to mængder er lige store?
Svar: To mængder er lige store, hvis de har de samme medlemmer.
Søge