Trigonometriske funktioner – definition og guide til sinus, cosinus og tangent
Lær trigonometriske funktioner: enkel guide til sinus, cosinus og tangent med forklaringer, formler og anvendelser — perfekt til studerende og hurtig repetition.
I matematik er de trigonometriske funktioner et sæt funktioner, som relaterer vinkler til siderne i en retvinklet trekant. Der findes mange trigonometriske funktioner, hvoraf de 3 mest almindelige er sinus, cosinus og tangent, efterfulgt af kotangent, sekant og kosekant. De tre sidstnævnte kaldes reciprokke trigonometriske funktioner, fordi de fungerer som reciprokke af andre funktioner. Sekant og kosecant anvendes sjældent.
Definitioner i en retvinklet trekant
- Sinus (sin): forholdet mellem den modstående katete og hypotenusen. Formel: sin(v) = modstående / hypotenuse.
- Cosinus (cos): forholdet mellem den hosliggende katete og hypotenusen. Formel: cos(v) = hosliggende / hypotenuse.
- Tangent (tan): forholdet mellem den modstående og den hosliggende katete. Formel: tan(v) = modstående / hosliggende = sin(v) / cos(v).
Unitcircle (enhedscirklen)
Trigonometriske funktioner kan også forstås via en enhedscirkel (cirkel med radius 1) med centrum i (0,0). For en vinkel v målt fra positiv x-akse gælder:
- cos(v) er x-koordinaten af punktet på cirklen.
- sin(v) er y-koordinaten af punktet på cirklen.
- tan(v) = sin(v)/cos(v) svarer til hældningen af linjen fra origo til punktet.
Domæne, værdimængde og perioder
- Domæne: sin og cos er defineret for alle reelle tal (hele talinjen). Tan er ikke defineret hvor cos(v) = 0 (fx v = π/2 + kπ).
- Værdimængde: sin(v) og cos(v) varierer i intervallet [-1, 1]. Tan(v) kan være alle reelle tal (−∞ til ∞), og har lodrette asymptoter ved de steder, hvor cos(v)=0.
- Perioder: sin og cos har periode 2π (360°). Tangent har periode π (180°).
Vigtige identiteter
- Pythagoræisk identitet: sin^2(v) + cos^2(v) = 1.
- Forhold: tan(v) = sin(v)/cos(v).
- Reciprokke funktioner: kotangent (cot) = cos/sin, sekant (sec) = 1/cos, kosekant (csc) = 1/sin.
- Summen- og differensformler: sin(a ± b) = sin a cos b ± cos a sin b; cos(a ± b) = cos a cos b ∓ sin a sin b.
- Dobbeltvinkel: sin(2a) = 2 sin a cos a; cos(2a) = cos^2 a − sin^2 a.
Specielle vinkler (hyppigt brugte værdier)
- v = 0°: sin = 0, cos = 1
- v = 30°: sin = 1/2, cos = √3/2
- v = 45°: sin = cos = √2/2
- v = 60°: sin = √3/2, cos = 1/2
- v = 90°: sin = 1, cos = 0
Inverterede funktioner
Der findes også inverse funktioner: arcsin, arccos og arctan, som bruges til at finde vinkler ud fra en trigonometrisk værdi. Bemærk, at disse funktioner normalt begrænses til et principalområde for at være entydige (fx arcsin : [−1,1] → [−π/2, π/2]).
Differentiation og integration (kort)
- d/dx sin x = cos x
- d/dx cos x = −sin x
- d/dx tan x = sec^2 x (hvor defineret)
- Integraler: ∫ sin x dx = −cos x + C, ∫ cos x dx = sin x + C, ∫ tan x dx = −ln|cos x| + C
Grafisk forståelse
Sinus- og cosinusfunktionernes grafer er bølgeformede: de har amplitude (maksimumsværdi) 1, periode 2π og skifter mellem top og bund symmetrisk. Tangensgrafen gentager sig hver π og har lodrette asymptoter ved værdier, hvor cos = 0.
Anvendelser
Trigonometriske funktioner bruges overalt i matematik, fysik og teknik: analyser af bølger og svingninger, vibrations- og lydanalyse, signalbehandling (Fourier-analyse), navigation, ingeniørberegninger og i geometriske beregninger, når vinkler og afstande indgår.
Praktisk regneeksempel
Givet en retvinklet trekant med hypotenuse 10 og en modstående katete på 6, beregnes:
- sin(v) = 6/10 = 0,6
- cos(v) = √(1 − sin^2(v)) = √(1 − 0,36) = √0,64 = 0,8
- tan(v) = sin(v)/cos(v) = 0,6/0,8 = 0,75
Disse grundlæggende regler og identiteter gør trigonometriske funktioner til stærke værktøjer til at forbinde vinkler og længder samt til at beskrive periodiske fænomener.
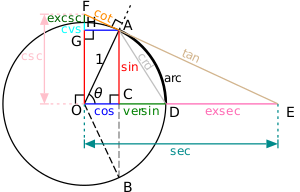
Alle trigonometriske funktioner for en hvilken som helst vinkel kan konstrueres ved hjælp af en cirkel med centrum i O og radius 1.

Trigonometriske funktioner: Sinus , cosinus , tangent , kosecant , sekant , kotangent
Definition
De trigonometriske funktioner kaldes undertiden også cirkelfunktioner. De er funktioner af en vinkel; de er vigtige, når man studerer trekanter, blandt mange andre anvendelser. Trigonometriske funktioner defineres almindeligvis som forhold mellem to sider af en retvinklet trekant, der indeholder vinklen, og kan tilsvarende defineres som længderne af forskellige linjestykker fra en enhedscirkel (en cirkel med radius 1).
Definitioner af retvinklede trekanter
For at definere de trigonometriske funktioner for vinklen A skal du starte med en retvinklet trekant, som indeholder vinklen A:
Vi bruger følgende navne for siderne i trekanten:
- Hypotenusen er den side, der er modsat den rette vinkel, eller defineret som den længste side i en retvinklet trekant, i dette tilfælde h.
- Den modsatte side er den side, der er modsat den vinkel, som vi er interesseret i, i dette tilfælde a.
- Den tilstødende side er den side, der er i kontakt med den vinkel, vi er interesseret i, og den rette vinkel, deraf navnet. I dette tilfælde er den tilstødende side b.
Alle trekanter antages at eksistere i euklidisk geometri, således at de indvendige vinkler i hver trekant summerer til π radianer (eller 180°); for en retvinklet trekant er de to ikke-højre vinkler derfor mellem nul og π/2 radianer. Læseren skal være opmærksom på, at de følgende definitioner strengt taget kun definerer de trigonometriske funktioner for vinkler i dette område. Vi udvider dem til hele sættet af reelle argumenter ved at bruge enhedscirklen eller ved at kræve visse symmetrier og at de skal være periodiske funktioner.
1) Sinus af en vinkel er forholdet mellem længden af den modsatte side og længden af hypotenusen. I vores tilfælde
sin A = modsatte hypotenuse = a h . {\displaystyle \sin A={\frac {\textrm {\textrm {modsat}}}{\textrm {hypotenuse}}}}={\frac {a}{h}}}. }
Bemærk, at dette forhold ikke afhænger af den valgte retvinklede trekant, så længe den indeholder vinklen A, da alle disse trekanter er ens.
Mængden af nulpunkter for sinus (dvs. de værdier af x {\displaystyle x}

{ n π | n ∈ Z } . {\displaystyle \left\{n\pi {\big |}n\in \mathbb {Z} \right\}. }
2) En vinkels cosinus er forholdet mellem længden af den tilstødende side og hypotenusenes længde. I vores tilfælde
cos A = tilstødende hypotenuse = b h . {\displaystyle \cos A={\frac {\textrm {\textrm {adjacent}}}{\textrm {hypotenuse}}}}={\frac {b}{h}}}. }
Mængden af nuller af cosinus er
{ π 2 + n π | n ∈ Z } . {\displaystyle \left\{{{\frac {\pi }{2}}}+n\pi {\bigg |}n\in \mathbb {Z} \right\}. }
3) Tangenten til en vinkel er forholdet mellem længden af den modsatte side og længden af den tilstødende side. I vores tilfælde
tan A = modsat tilstødende = a b . {\displaystyle \tan A={\frac {\textrm {\textrm {modsat}}}{\textrm {nærliggende}}}}={\frac {a}{b}}}. }
Mængden af tangentens nulpunkt er
{ n π | n ∈ Z } . {\displaystyle \left\{n\pi {\big |}n\in \mathbb {Z} \right\}. }
Det samme sæt af sinusfunktionen siden
tan A = sin A cos A . {\displaystyle \tan A={\frac {\sin A}{\cos A}}. }
De resterende tre funktioner kan bedst defineres ved hjælp af de tre ovennævnte funktioner.
4) Kosecanten csc(A) er den multiplikative omvendte af sin(A), dvs. forholdet mellem hypotenusens længde og den modsatte sides længde:
csc A = hypotenuse modsat = h a {\displaystyle \csc A={\frac {\textrm {hypotenuse}}}{\textrm {opposite}}}}={\frac {h}{a}}}}
5) Sekanten sec(A) er den multiplikative inverse af cos(A), dvs. forholdet mellem hypotenusens længde og den tilstødende sides længde:
sec A = hypotenuse tilstødende = h b {\displaystyle \sec A={\frac {\textrm {hypotenuse}}{\textrm {adjacent}}}}={\frac {h}{b}}}}
6) Kotangenten cot(A) er den multiplikative omvendte af tan(A), dvs. forholdet mellem længden af den tilstødende side og længden af den modsatte side:
cot A = tilstødende modsat = b a {\displaystyle \cot A={\frac {\textrm {adjacent}}{\textrm {opposite}}}}={\frac {b}{a}}}}
Definitioner ved hjælp af potenserier
Man kan også definere de trigonometriske funktioner ved hjælp af potensrækker:
sin x = x - x - x 3 3 3 ! + x 5 5 ! - x 7 7 ! + ⋯ = ∑ n = 0 ∞ ( - 1 n ( - 1 ) x 2 n + 1 ( 2 n + 1 ) ! {\displaystyle \sin x=x-{\frac {x^{3}}}{3!}}+{\frac {x^{5}}}{5!}}-{\frac {x^{7}}}{7!}}+\cdots =\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n+1}}}{(2n+1)!}}}
cos x = 1 - x 2 2 2 ! + x 4 4 ! - x 6 6 ! + ⋯ = ∑ n = 0 ∞ ( - 1 ) n x 2 n x 2 n ( 2 n ) ! {\displaystyle \cos x=1-{\frac {x^{2}}}{2!}}+{\frac {x^{4}}}{4!}}-{\frac {x^{6}}}{6!}}+\cdots =\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n}}}{(2n)!}}}
og definere tangent, kotangent, sekant og kosecant ved hjælp af identiteter, se nedenfor.
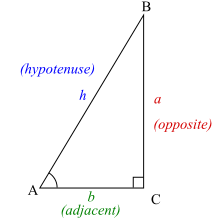
En retvinklet trekant indeholder altid en vinkel på 90° (π/2 radianer), her mærket C. Vinklerne A og B kan variere. Trigonometriske funktioner angiver forholdet mellem sidelængderne og de indvendige vinkler i en retvinklet trekant.
Identiteter
Nogle vigtige identiteter:
tan x = sin x cos x {\displaystyle \tan x={\frac {\\sin x}{\cos x}}}
cot x = cos x sin x {\displaystyle \cot x={\frac {\cos x}{\sin x}}}
sec x = 1 cos x {\displaystyle \sec x={\frac {1}{\cos x}}}
csc x = 1 sin x {\displaystyle \csc x={\frac {1}{\sin x}}}
sin 2 x + cos 2 x = 1 {\displaystyle \sin ^{2}x+\cos ^{2}x=1}
sin 2 x = 2 sin x cos x {\displaystyle \sin 2x=2\sin x\cos x\cos x}
cos 2 x = cos x cos x cos x - sin x sin x = cos 2 x - sin 2 x = 2 cos 2 x - 1 = 1 - 2 sin 2 x {\displaystyle \cos 2x=\cos x\cos x\cos x\cos x-\sin x\sin x\sin x=\cos ^{2}x-\sin ^{2}x=2\cos ^{2}x-1=1-2\sin ^{2}x}
tan 2 x = 2 tan x 1 - tan 2 x {\displaystyle \tan 2x={\frac {2\tan x}{1-\tan ^{2}x}}}}
sin ( x ± y ) = sin x cos y ± cos x sin y {\displaystyle \sin \left(x\pm y\right)=\sin x\cos y\pm \cos x\sin y}
cos ( x ± y ) = cos x cos y ∓ sin x sin y {\displaystyle \cos \left(x\pm y\right)=\cos x\cos y\mp \sin x\sin y}
tan ( x ± y ) = tan x ± tan y 1 ∓ tan x tan y {\displaystyle \tan \left(x\pm y\right)={\frac {\tan x\pm \tan y}{1\mp \tan x\tan x\tan y}}} 
Hyperbolske funktioner
De hyperbolske funktioner ligner de trigonometriske funktioner, idet de har meget ens egenskaber. De er defineret ud fra den eksponentielle funktion, som er baseret på konstanten e.
- Hyperbolisk sinus:
sinh x = e x - e - x 2 = e 2 x - 1 2 e x = 1 - e - 2 x 2 e - x . {\displaystyle \sinh x={\frac {e^{x}-e^{-x}}}{2}}}={\frac {e^{2x}-1}{2e^{x}}}}={\frac {1-e^{-2x}}}{2e^{-x}}}. }
- Hyperbolisk cosinus:
cosh x = e x + e - x 2 = e 2 x + 1 2 e x = 1 + e - 2 x 2 e - x . {\displaystyle \cosh x={\frac {e^{x}+e^{-x}}}{2}}}={\frac {e^{2x}+1}{2e^{x}}}={\frac {1+e^{-2x}}}{2e^{-x}}}. }
- Hyperbolisk tangent:
tanh x = sinh x cosh x = e x - e - x e x + e - x = e 2 x - 1 e 2 x + 1 = 1 - e - 2 x 1 + e - 2 x . {\displaystyle \tanh x={\frac {\sinh x}{\cosh x}}={\frac {e^{x}-e^{-x}}}{e^{x}+e^{-x}}}}={\frac {e^{2x}-1}{e^{2x}+1}}}={\frac {1-e^{-2x}}}{1+e^{-2x}}}. }
- Hyperbolisk cotangent:
coth x = cosh x sinh x = e x + e - x e x - e - x = e 2 x + 1 e 2 x - 1 = 1 + e - 2 x 1 - e - 2 x , x ≠ 0. {\displaystyle \coth x={\frac {\cosh x}{\sinh x}}={\frac {e^{x}+e^{-x}}}{e^{x}-e^{-x}}}}={\frac {e^{2x}+1}{e^{2x}-1}}}={\frac {1+e^{-2x}}}{1-e^{-2x}}}},\qkvad x\neq 0.}
- Hyperbolisk sekant:
sech x = 1 cosh x = 2 e x + e - x = 2 e x e 2 x e 2 x + 1 = 2 e - x 1 + e - 2 x . {\displaystyle \operatornavn {sech} \,x={\frac {1}{\cosh x}}}={\frac {2}{e^{x}+e^{-x}}}}={\frac {2e^{{x}}}{e^{2x}}+1}}}={\frac {2e^{-x}}{1+e^{-2x}}}}. }
- Hyperbolisk kosecant:
csch x = 1 sinh x = 2 e x - e - x = 2 e x e 2 x e 2 x - 1 = 2 e - x 1 - e - 2 x , x ≠ 0. {\displaystyle \operatorname {csch} \,x={\frac {1}{\sinh x}}}={\frac {2}{e^{x}-e^{-x}}}}={\frac {2e^{{x}}}{e^{2x}}-1}}={\frac {2e^{-x}}{1-e^{-2x}}}},\qquad x\neq 0.} 
Relaterede sider
Søge






















