Frekvensfordeling: Definition, typer og eksempler i statistik
Frekvensfordeling forklaret: definition, typer og konkrete eksempler — forstå diskrete og kontinuerte data, histogrammer og hyppighedstabeller for bedre statistisk indsigt.
I statistik er en frekvensfordeling en liste over de værdier, som en variabel har i en stikprøve. Det er normalt en liste, der er ordnet efter mængde. Den viser antallet af gange, hver værdi forekommer. Hvis 100 personer f.eks. vurderer deres enighed med et udsagn på en fempunkts Likert-skala, hvor 1 angiver stærk enighed og 5 stærk uenighed, kan frekvensfordelingen af deres svar f.eks. se således ud:
- 1: 30 svar (absolut hyppighed)
- 2: 25 svar
- 3: 20 svar
- 4: 15 svar
- 5: 10 svar
Denne enkle tabel har to ulemper. Når en variabel kan antage kontinuerte værdier i stedet for diskrete værdier, eller når antallet af mulige værdier er for stort, er det vanskeligt, hvis det ikke er umuligt, at konstruere tabellen. I sådanne tilfælde anvendes et lidt andet skema baseret på værdispektret. Hvis vi f.eks. betragter højden af eleverne i en klasse, kan hyppighedstabellen se ud som nedenfor.
Typer af frekvensfordelinger
- Absolut hyppighed: Det antal observationer, der falder i en given kategori eller værdi (fx 30 personer valgte 1).
- Relativ hyppighed: Andelen af observationer i forhold til totalen, ofte angivet som en brøk eller procent. Formel: relativ hyppighed = absolut hyppighed / n.
- Akkumuleret (kumulativ) hyppighed: Summen af absolutte hyppigheder op til og med en given kategori. Bruges til at finde percentiler og medianen.
- Gruppet (interval-) frekvensfordeling: Bruges for kontinuerte data ved at gruppere værdier i klasser (fx 150–159 cm, 160–169 cm).
Hvordan man laver en frekvensfordeling
- Beslut om variablen er diskret eller kontinuert.
- Tæl observationerne for hver unik værdi (diskret) eller i hvert interval (kontinuert).
- Beregn relative hyppigheder (og evt. procentsatser) ved at dividere med totalen n.
- Beregn akkumulerede hyppigheder hvis relevant (fx for at bestemme median eller percentiler).
- For grupperede data: vælg antal klasser og klassebredde. En tommelfingerregel er 5–20 klasser; Sturges' regel foreslår k ≈ 1 + log2(n) som en startværdi.
Eksempel på grupperet frekvensfordeling (højder)
Antag en klasse med 20 elever fordelt i disse klasser:
- 150–159 cm: 4 elever (midtpunkt 154,5)
- 160–169 cm: 8 elever (midtpunkt 164,5)
- 170–179 cm: 6 elever (midtpunkt 174,5)
- 180–189 cm: 2 elever (midtpunkt 184,5)
Estimeret gennemsnit for grupperede data beregnes ved at gange hvert klasses midtpunkt med klassens hyppighed, summere og dividere med n:
Gennemsnit ≈ (154,5·4 + 164,5·8 + 174,5·6 + 184,5·2) / 20 = 3350 / 20 = 167,5 cm
Grafiske fremstillinger
- Søjlediagram (bar chart): Velegnet til diskrete kategorier (fx Likert-skala). Højde på søjler viser absolut eller relativ hyppighed.
- Histogram: Bruges til grupperede kontinuerte data. Søjlerne berører hinanden; areal svarer til hyppighed.
- Frekvenspolygon: Linje, som forbinder midtpunkterne af histogrammets søjler — nyttig til sammenligning af fordelinger.
- Ogive (kumulativ frekvenskurve): Viser akkumuleret relativ eller absolut hyppighed og bruges til at aflæse percentiler.
Anvendelser og praktiske råd
- Frekvensfordelinger er grundlaget for beskrivende statistik: de afslører form (symmetri/skævhed), antal toppe (modalitet) og eventuelle outliers.
- Ved store datasæt anbefales grupperede fordelinger for at gøre mønstre tydelige.
- Vælg klassebredde, så klasserne bliver meningsfulde og hver klasse får et passende antal observationer. For smalle klasser kan skabe støj; for brede klasser mister man information.
- Ved rapportering: medtag altid n (antal observationer) og angiv om hyppigheder er absolutte eller relative (procenter) for klarhed.
Afsluttende bemærkninger
En korrekt udarbejdet frekvensfordeling gør data mere overskuelige og er ofte det første skridt i dataanalyse. Fra en simpel tabel over Likert-svar til grupperede fordelinger af kontinuerte målinger giver frekvensfordelinger vigtig indsigt i datastrukturen og danner grundlag for videre analyse som beregning af middelværdi, median, varians og grafiske fremstillinger.

Dette er Kinas befolkningspyramide for år 2005.
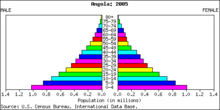
Eksempel på en (absolut) frekvensfordeling. Dette er befolkningspyramiden for Angola for 2005.
Applikationer
Det er meget nemmere at administrere og arbejde med frekvenstabellerede data end at arbejde med rå data. Der findes enkle algoritmer til at beregne median, middelværdi (statistik), standardafvigelse osv. fra disse tabeller.
Statistisk hypotesetestning er baseret på vurderingen af forskelle og ligheder mellem frekvensfordelinger. Denne vurdering omfatter mål for central tendens eller gennemsnit, f.eks. middelværdi og median, og mål for variabilitet eller statistisk spredning, f.eks. standardafvigelse eller varians.
En frekvensfordeling siges at være skæv, når dens gennemsnit og median er forskellige. En frekvensfordelings kurtose er koncentrationen af scoringer ved middelværdien, eller hvor stor en spids fordelingen er, hvis den afbildes grafisk - f.eks. i et histogram. Hvis fordelingen er mere toppet end normalfordelingen, siges den at være leptokurtisk; hvis den er mindre toppet, siges den at være platykurtisk.
Frekvensfordelinger bruges også i frekvensanalyser til at knække koder og henviser til den relative hyppighed af bogstaver i forskellige sprog.
| ||||||||||||||||||||||||
| ||||||||||||||||||||||||
| ||||||||||||||||||||||||
| ||||||||||||||||||||||||
| ||||||||||||||||||||||||
| ||||||||||||||||||||||||
| ||||||||||||||||||||||||
|
Spørgsmål og svar
Spørgsmål: Hvad er en frekvensfordeling?
A: En frekvensfordeling er en liste over de værdier, som en variabel antager i en stikprøve, ordnet efter mængde. Den viser, hvor mange gange hver værdi forekommer.
Spørgsmål: Hvordan kan frekvensfordelingen af svarene på en fempunkts Likert-skala se ud?
Svar: Frekvensfordelingen af svarene på en fempunkts Likert-skala kan ligne en simpel tabel, der viser antallet af personer, der har vurderet hvert punkt på skalaen.
Sp: Hvad er to ulemper ved at bruge denne type tabel?
A: To ulemper ved at bruge denne type tabel er, at det kan være vanskeligt eller endog umuligt at bruge den, når der er tale om kontinuerte værdier, eller når der er for mange mulige værdier.
Spørgsmål: Hvordan er denne ordning anderledes, når der er tale om kontinuerlige værdier eller et stort antal mulige værdier?
Svar: Når der er tale om kontinuerlige værdier eller et stort antal mulige værdier, kan der i stedet anvendes en lidt anderledes ordning baseret på værdispænd.
Spørgsmål: Hvordan kan en hyppighedstabel for elevernes højde se ud?
Svar: Hyppighedstabellen for elevhøjder kan vise intervaller, og hvor mange elever der falder inden for hvert interval.
Spørgsmål: Hvilke oplysninger giver frekvensfordelingen?
Svar: Frekvensfordelingen giver oplysninger om, hvor ofte visse variabler forekommer i stikprøver, og hvordan de er fordelt på tværs af disse stikprøver.
Søge