Lineær regression | en måde at se på, hvordan noget ændrer sig, når andre ting ændrer sig ved hjælp af matematik
Lineær regression er en måde at se på, hvordan noget ændrer sig, når andre ting ændrer sig, ved hjælp af matematik. En lineær regression bruger en afhængig variabel og en eller flere forklarende variabler til at skabe en lige linje. Denne lige linje er kendt som en "regressionslinje".
Lineær regression var den første af mange måder at udføre regressionsanalyse på. Det skyldes, at modeller, der afhænger lineært af deres ukendte parametre, er lettere at tilpasse end modeller, der er ikke-lineært relateret til deres parametre. En anden fordel ved lineær regression er, at de statistiske egenskaber ved de resulterende estimatorer er lettere at bestemme.
Lineær regression har mange praktiske anvendelsesmuligheder. De fleste anvendelser falder ind under en af følgende to brede kategorier:
- Lineær regression kan bruges til at tilpasse en forudsigelsesmodel til et sæt observerede værdier (data). Dette er nyttigt, hvis målet er forudsigelse, prognose eller reduktion. Hvis der efter udviklingen af en sådan model gives en yderligere værdi af X uden den tilhørende værdi af y, kan den tilpassede model anvendes til at lave en forudsagt værdi af y (skrevet som
- Med en variabel y og en række variabler X1 , ..., Xp , der kan være relateret til y, kan lineær regressionsanalyse anvendes til at kvantificere styrken af forholdet mellem y og Xj , til at vurdere, hvilken Xj der slet ikke har nogen sammenhæng med y, og til at identificere, hvilke delmængder af Xj der indeholder overflødige oplysninger om y.
Lineære regressionsmodeller forsøger at gøre den lodrette afstand mellem linjen og datapunkterne (dvs. residualerne) så lille som muligt. Dette kaldes "tilpasning af linjen til dataene". Ofte forsøger lineære regressionsmodeller at minimere summen af residualernes kvadrater (mindste kvadrater), men der findes også andre måder at tilpasse på. De omfatter minimering af "manglende tilpasning" i en anden norm (som ved regression med mindste absolutte afvigelser) eller minimering af en straffet version af tabsfunktionen for mindste kvadrater som ved ridge-regression. Den mindste kvadraters metode kan også bruges til at tilpasse modeller, der ikke er lineære. Som skitseret ovenfor er udtrykkene "mindste kvadraters" og "lineær model" tæt forbundet, men de er ikke synonymer.
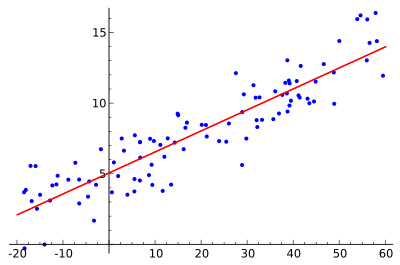
Ideen er at finde den røde kurve, og de blå punkter er de faktiske prøver. Med lineær regression kan alle punkter forbindes ved hjælp af en enkelt, lige linje. I dette eksempel anvendes simpel lineær regression, hvor kvadratet på afstanden mellem den røde linje og hvert prøvepunkt minimeres.
Anvendelse
Økonomi
Lineær regression er det vigtigste analytiske værktøj inden for økonomi. Det bruges f.eks. til at gætte forbrugsudgifter, udgifter til faste investeringer, lagerinvesteringer, køb af et lands eksportvarer, udgifter til import, efterspørgsel efter likvide aktiver, efterspørgsel efter arbejdskraft og arbejdsudbud.
Relaterede sider
- Kurvetilpasning
- Logistisk regression
- Almindelige mindste kvadrater
Spørgsmål og svar
Spørgsmål: Hvad er lineær regression?
A: Lineær regression er en måde at se på, hvordan noget ændrer sig, når andre ting ændrer sig, ved hjælp af matematik. Den bruger en afhængig variabel og en eller flere forklarende variabler til at skabe en lige linje, kendt som "regressionslinjen".
Spørgsmål: Hvad er fordelene ved lineær regression?
Svar: De modeller, der afhænger lineært af deres ukendte parametre, er lettere at tilpasse end modeller, der er ikke-lineært afhængige af deres parametre. Desuden er de statistiske egenskaber ved de resulterende estimatorer lettere at bestemme.
Spørgsmål: Hvad er nogle praktiske anvendelser af lineær regression?
Svar: Lineær regression kan bruges til at tilpasse en forudsigelsesmodel til observerede værdier (data) med henblik på at foretage forudsigelser, prognoser eller reduktioner. Den kan også bruges til at kvantificere styrken af sammenhænge mellem variabler og identificere delmængder af data, der indeholder overflødige oplysninger om en anden variabel.
Spørgsmål: Hvordan forsøger lineære regressionsmodeller at minimere fejl?
Svar: Lineære regressionsmodeller forsøger at gøre den lodrette afstand mellem linjen og datapunkterne (residualerne) så lille som muligt. Dette gøres ved at minimere enten summen af residualernes kvadrater (mindste kvadrater), manglende tilpasning i en anden norm (mindste absolutte afvigelser) eller ved at minimere en straffet version af mindste kvadraters tabsfunktion (ridge-regression).
Spørgsmål: Er det muligt for lineære regressionsmodeller ikke at være baseret på mindste kvadrater?
Svar: Ja, det er muligt, at lineære regressionsmodeller ikke er baseret på mindste kvadraters metode, men i stedet anvender metoder som f.eks. minimering af manglende tilpasning i en anden norm (mindste absolutte afvigelser) eller minimering af en straffet version af mindste kvadraters tabsfunktion (ridge-regression).
Spørgsmål: Er "lineær model" og "mindste kvadrater" synonymer?
Svar: Nej, de er ikke synonymer. Selv om de er tæt forbundet, henviser "lineær model" specifikt til at bruge en lige linje, mens "mindste kvadraters" specifikt henviser til at forsøge at minimere fejl ved at sikre, at der er minimal lodret afstand mellem linjen og datapunkterne.
Søge
