AlegsaOnline.com

Venn-diagram: Definition, historie og anvendelser i logik, statistik og datalogi

Venn-diagram: Få klar definition, historisk baggrund og praktiske anvendelser i logik, statistik og datalogi — lær at illustrere mængder, relationer og sandsynlighed.

Forfatter: Leandro Alegsa

08-01-2026

Et Venn-diagram er et diagram, der viser den logiske sammenhæng mellem mængder. De blev populariseret af John Venn i 1880'erne og er nu meget udbredt. De bruges til at undervise i elementær mængdelære og til at illustrere enkle mængdeforhold inden for sandsynlighed, logik, statistik, lingvistik og datalogi. I et Venn-diagram anvendes lukkede kurver tegnet på et plan til at repræsentere mængder. Meget ofte er disse kurver cirkler eller ellipser.

Lignende idéer var blevet foreslået før Venn. Christian Weise i 1712 (Nucleus Logicoe Wiesianoe) og Leonhard Euler (Breve til en tysk prinsesse) i 1768 kom f.eks. med lignende idéer. Idéen blev populariseret af Venn i Symbolic Logic, kapitel V "Diagrammatic Representation", 1881.

Hvad viser et Venn-diagram?

Et Venn-diagram deler planet i områder, hvor hver kurve repræsenterer en mængde. De enkelte områder svarer til kombinationer af medlemsskaber:

Forening (A ∪ B): alle elementer, der er i mindst én af mængderne.
Snit (A ∩ B): elementer, der er i begge mængder samtidigt.
Differens (A \ B): elementer i A, men ikke i B.
Komplement (A^c): elementer udenfor A i universet under betragtning.

For to mængder tegnes normalt to overlappende cirkler; for tre mængder tre overlappende cirkler, som tilsammen deler planet i otte (2^3) disjunkte regioner. Generelt findes der 2^n mulige regioner for n mængder, og et fuldt Venn-diagram viser alle disse regioner — også dem, som kan være tomme.

Forskellen mellem Venn- og Euler-diagram

Det er vigtigt at skelne mellem Venn-diagrammer og Euler-diagrammer. Et Euler-diagram viser kun de faktisk eksisterende forhold mellem mængderne (tomme intersectioner udelades), mens et Venn-diagram formelt viser alle mulige kombinationer for de valgte mængder, uanset om nogle af dem er tomme. Derfor kan Venn-diagrammer være mere systematiske til at vise alle logiske tilfælde, mens Euler-diagrammer ofte er enklere og mere præcise, når nogle kombinationer ikke forekommer.

Anvendelser

Venn-diagrammer bruges i mange fag og sammenhænge:

Uddannelse og logik: Til at illustrere logiske relationer, sætningsstruktur i syllogismer og mængdelæreforklaringer.
Sandsynlighed: Hjælper med at visualisere begivenheder og beregne sandsynligheder, f.eks. P(A ∪ B) = P(A) + P(B) − P(A ∩ B).
Statistik og datavidenskab: Bruges i explorativ dataanalyse til at vise overlap mellem datasæt, krydsklasser eller funktioner.
Datalogi: Visualisering af mængder i databaser, bitmasks, søgeresultater og logiske operationer (AND, OR, NOT).
Lingvistik: Til at vise semantiske overlap mellem begreber, sætningskonstruktioner eller fonologiske klasser.
Praktiske anvendelser: Bruges i beslutningstagning, kravspecifikation, markedssegmentering og til at forklare komplekse overlap til ikke-specialister.

Udvidelser og varianter

Når antallet af mængder vokser, bliver det vanskeligt at tegne klare cirkler, der viser alle 2^n regioner. For n > 3 anvendes ofte andre kurver eller mere avancerede konstruktioner:

Symmetriske Venn-diagrammer (ofte konstrueret med polygoner eller specielle kurver) for 4, 5 eller flere mængder.
Area-proportionale Venn-diagrammer, hvor arealet af hvert område svarer til mængdernes kardinaliteter eller sandsynligheder — nyttigt når man vil sammenligne størrelser visuelt.
Interaktive og digitale værktøjer, som kan fremhæve regioner og vise talværdier dynamisk.

Begrænsninger

Selvom Venn-diagrammer er intuitive, har de også begrænsninger:

De repræsenterer ikke altid størrelser korrekt, medmindre de er lavet area-proportionale.
De bliver hurtigt uoverskuelige ved mange mængder (n stort), og informationstæthed kan bli' høj.
Visuelle overlap kan være misvisende, hvis kurver ikke er præcist konstruerede.

Hvordan læser man et Venn-diagram?

Følgende fremgangsmåde hjælper til at aflæse et diagram korrekt:

Identificer hver cirkel/kurve og dens tilsvarende mængde (etiket).
Find områder, hvor kurver overlapper — disse svarer til snit.
Læg mærke til områder udenfor alle kurver — det er komplementet ift. det betragtede univers.
Ved tre mængder: tæl eller angiv elementer i hver af de otte områder (A kun, B kun, C kun, A∩B kun osv.).

Venn-diagrammer er et enkelt, visuelt og effektivt redskab til at tænke systematisk over mængder, relationer og logik. De kombinerer pædagogisk klarhed med praktisk anvendelighed i mange fagområder, men bør anvendes med opmærksomhed på deres begrænsninger og på, hvordan arealer fortolkes.

Glasmosaikvindue i Cambridge, hvor John Venn studerede. Det viser et Venn-diagram.

Eksempel

I det følgende eksempel anvendes to sæt, A og B, som her er repræsenteret som farvede cirkler. Den orange cirkel, sæt A, repræsenterer alle levende væsener, der er tobenede. Den blå cirkel, sæt B, repræsenterer de levende væsener, der kan flyve. Hver enkelt type væsen kan forestilles som et punkt et sted i diagrammet. Levende væsener, der både kan flyve og har to ben - f.eks. papegøjer - er således i begge sæt og svarer derfor til punkter i det område, hvor de blå og orange cirkler overlapper hinanden. Dette område indeholder alle (og kun) sådanne levende væsener.

Mennesker og pingviner er tobenede og befinder sig derfor i den orange cirkel, men da de ikke kan flyve, befinder de sig i den venstre del af den orange cirkel, hvor den ikke overlapper med den blå cirkel. Myg har seks ben og kan flyve, så punktet for myg er i den del af den blå cirkel, som ikke overlapper den orange cirkel. Skabninger, der ikke har to ben og ikke kan flyve (f.eks. hvaler og edderkopper), ville alle være repræsenteret af punkter uden for begge cirkler.

Det kombinerede område af mængderne A og B kaldes foreningen af A og B, angivet ved A ∪ B. Foreningen indeholder i dette tilfælde alle levende væsener, der enten er tobenede eller kan flyve (eller begge dele). Området i både A og B, hvor de to sæt overlapper hinanden, kaldes skæringspunktet mellem A og B, angivet ved A ∩ B. For eksempel er skæringspunktet mellem de to sæt ikke tomt, fordi der er punkter, der repræsenterer væsener, som er i både den orange og den blå cirkel.

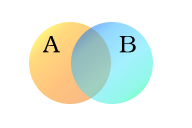
Sæt A (væsener med to ben) og B (væsener, der kan flyve)

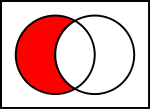
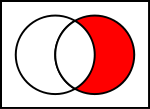
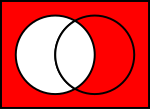
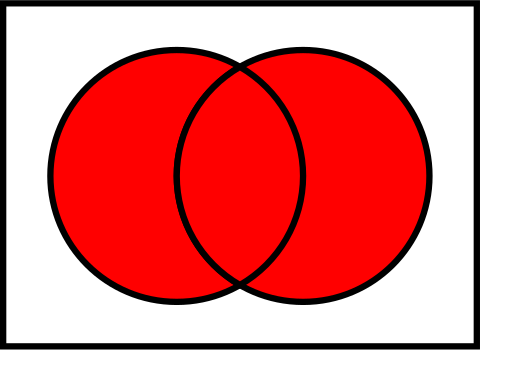
Venn-diagrammer af almindelige operationer på mængder

I illustrationerne nedenfor viser den venstre cirkel sæt A {\displaystyle A} $A$ og den højre cirkel sæt B {\displaystyle B} $B$ . Resultaterne af operationerne er vist som farvede områder.

Relaterede sider

Eksklusiv disjunktion
Inkluderende disjunktion

Spørgsmål og svar

Sp: Hvad er et Venn-diagram?

A: Et Venn-diagram er et diagram, der viser den logiske sammenhæng mellem mængder. Det bruger lukkede kurver tegnet på et plan, normalt cirkler eller ellipser, til at repræsentere mængder.

Sp: Hvem har gjort Venn-diagrammer populære?

Svar: John Venn populariserede Venn-diagrammer i 1880'erne.

Spørgsmål: Hvad bruges de til?

A: De bruges til at undervise i elementær mængdelære og til at illustrere enkle mængdeforhold inden for sandsynlighed, logik, statistik, lingvistik og datalogi.

Spørgsmål: Hvem foreslog lignende idéer før John Venn?

A: Christian Weise foreslog lignende idéer i 1712 med sin Nucleus Logicoe Wiesianoe, og Leonhard Euler foreslog dem i Breve til en tysk prinsesse i 1768.

Sp: Hvornår udgav John Venn Symbolic Logic?

Svar: John Venn udgav Symbolic Logic i 1881.

Spørgsmål: I hvilket kapitel af Symbolic Logic blev ideen om et Venn-diagram populariseret af John Venn?

Svar: John Venn gjorde ideen om et Venn-diagram populær i kapitel 5 "Diagrammatic Representation" i Symbolic Logic.

Spørgsmål: Hvordan blev disse idéer repræsenteret før opfindelsen af den moderne version af Venn-diagrammet?

A: Før opfindelsen af den moderne version af V enn-diagrammet blev disse idéer repræsenteret ved hjælp af lukkede kurver tegnet på et plan, f.eks. cirkler eller ellipser.