Punktprodukt

Definition

Punktproduktet af to vektorer a = [a₁ , a₂ , ..., a_n ] og b = [b₁ , b₂ , ..., b_n ] er defineret som:

a ⋅ b = ∑ i = 1 n a i b i = a 1 b 1 + a 2 b 2 + ⋯ + a n b n {\displaystyle \mathbf {a} \cdot \mathbf {b} =\sum _{i=1}^{n}a_{i}b_{i}b_{i}=a_{1}b_{1}+a_{2}b_{2}+\cdots +a_{n}b_{n}}

hvor Σ betegner summationsnotation (summen af alle termerne) og n er dimensionen af vektorrummet.

I dimension 2 er prikproduktet af vektorerne [a,b] og [c,d] ac + bd. På samme måde er prikproduktet af vektorerne [a,b,c] og [d,e,f] i dimension 3 ad + be + cf. F.eks. er prikproduktet af to tredimensionale vektorer [1, 3, -5] og [4, -2, -1]

[ 1 , 3 , - 5 ] ⋅ [ 4 , - 2 , - 1 ] = ( 1 × 4 ) + ( 3 × ( - 2 ) ) + ( ( ( - 5 ) × ( - 1 ) ) = ( 4 ) - ( 6 ) + ( 5 ) = 3. {\displaystyle [1,3,-5]\cdot [4,-2,-1]=(1\ gange 4)+(3\ gange (-2))+((-5)\ gange (-1))=(4)-(6)+(5)=3.}

Geometrisk fortolkning

I euklidisk geometri er punktproduktet, længden og vinklen relateret til hinanden. For en vektor a er prikproduktet a - a kvadratet på længden af a, eller

a ⋅ a = ‖ a ‖ a ‖ 2 {\displaystyle {\mathbf {a} \cdot \mathbf {a} }=\left\|\mathbf {a} \right\|^{2}}}

hvor ||a||| angiver længden (størrelsen) af a. Mere generelt, hvis b er en anden vektor

a ⋅ b = ‖ a ‖ ‖ ‖ b ‖ cos θ {\displaystyle \mathbf {a} \cdot \mathbf {b} =\left\|\mathbf {a} \right\|\,\left\||\mathbf {b} \right\|\cos \theta \,}

hvor ||a|| og ||b|| betegner længden af a og b, og θ er vinklen mellem dem.

Denne formel kan omformuleres til at bestemme størrelsen af vinklen mellem to vektorer, der ikke er nul:

θ = arccos ( a ⋅ b ‖ a ‖ ‖ ‖ b ‖ ) {\displaystyle \theta =\arccos \left({\frac {{\mathbf {a}}}\cdot {\mathbf {b}}}{\left\|{\mathbf {a}}}\right\|\left\|{\mathbf {b}}}right\|}}}\right)}

Man kan også først omdanne vektorerne til enhedsvektorer ved at dividere dem med deres størrelsesorden:

a ^ = a ‖ a ‖ a ‖ {\displaystyle {\boldsymbol {\hat {a}}}={\frac {\mathbf {a}}{\left\|{{\mathbf {a}}\right\}}}

så er vinklen θ givet ved

θ = arccos ( a ^ ⋅ b ^ ) {\displaystyle \theta =\arccos({\boldsymbol {\hat {a}}}}\cdot {\boldsymbol {\hat {b}}}})}

Da cosinus af 90° er nul, er prikproduktet af to ortogonale (vinkelrette) vektorer altid nul. Desuden kan to vektorer kun betragtes som ortogonale, hvis og kun hvis deres punktprodukt er nul, og de begge har en længde, der ikke er nul. Denne egenskab giver en enkel metode til at teste betingelsen om ortogonalitet.

Nogle gange bruges disse egenskaber også til at definere prikproduktet, især i 2 og 3 dimensioner; denne definition svarer til ovenstående. I højere dimensioner kan formlen anvendes til at definere begrebet vinkel.

De geometriske egenskaber afhænger af, at grundlaget er ortonormalt, dvs. at det består af parvis vinkelrette vektorer med en enhedslængde.

Skalar projektion

Hvis både a og b har længde 1 (dvs. de er enhedsvektorer), er deres punktprodukt blot cosinus af vinklen mellem dem.

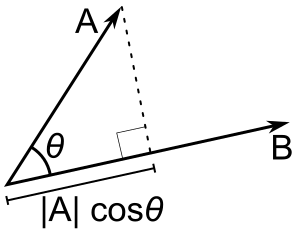
Hvis kun b er en enhedsvektor, giver prikproduktet a - b |a| cos(θ), dvs. størrelsen af projektionen af a i b's retning, med et minustegn, hvis retningen er modsat. Dette kaldes den skalære projektion af a på b eller den skalære komponent af a i retning af b (se figuren). Denne egenskab ved punktproduktet har flere nyttige anvendelser (se f.eks. næste afsnit).

Hvis hverken a eller b er en enhedsvektor, vil størrelsen af projektionen af a i retning af b f.eks. være a - (b / |b|), da enhedsvektoren i retning af b er b / |b|.

Rotation

En rotation af den ortonormale basis, som vektoren a er repræsenteret ved, opnås ved at multiplicere a med en rotationsmatrix R. Denne matrixmultiplikation er blot en kompakt repræsentation af en række punktprodukter.

Lad f.eks.

• B₁ = {x, y, z} og B₂ = {u, v, w} er to forskellige ortonormale baser af det samme rum R³ , hvor B₂ opnås ved blot at rotere B₁ ,
• a₁ = (a_x , a_y , a_z ) repræsenterer vektor a i form af B₁ ,
• a₂ = (a_u , a_v , a_w ) repræsenterer den samme vektor i form af den drejede basis B₂ ,
• u₁ , v₁ , w₁ er de roterede basisvektorer u, v, w repræsenteret ved B₁ .

Derefter foretages rotationen fra B₁ til B₂ på følgende måde:

a 2 = R a 1 = [ u x u y u z v x v y v z w x w y w z ] [ a x a y a z ] = [ u 1 ⋅ a 1 v 1 ⋅ a 1 w 1 ⋅ a 1 w 1 ⋅ a 1 ] = [ a u a v a w ] . {\displaystyle {\mathbf {a}}_{2}={\mathbf {Ra}}_{1}={\begin{bmatrix}u_{x}&u_{y}&u_{z}\\v_{x}&v_{y}&v_{z}\\w_{x}&w_{y}&w_{z}\end{bmatrix}}{\begin{bmatrix}a_{x}\\a_{y}\\a_{z}\end{bmatrix}}={\begin{bmatrix}{\mathbf {u}}_{1}\cdot {\mathbf {a}}_{1}\\{\mathbf {v}}_{1}\cdot {\mathbf {a}}}_{1}\\{mathbf {w}}_{1}\cdot {\mathbf {a}}}_{1}\end{bmatrix}}}={{begin{bmatrix}a_{u}\a_{v}\\\a_{w}\end{bmatrix}}}. }

Bemærk, at rotationsmatrixen R er sammensat ved at bruge de roterede basisvektorer u₁ , v₁ , v₁ som rækker, og disse vektorer er enhedsvektorer. Ra₁ består pr. definition af en række punktprodukter mellem hver af de tre rækker i R og vektor a₁ . Hvert af disse punktprodukter bestemmer en skalarisk komponent af a i retning af en roteret basisvektor (se foregående afsnit).

Hvis₁ er en rækkevektor i stedet for en kolonnevektor, skal R indeholde de roterede basisvektorer i sine kolonner og skal eftermultiplicere₁ :

a 2 = a 1 R = [ a x a y a z ] [ u x v x w x x u y v y w y u z v z w z ] = [ u 1 ⋅ a 1 v 1 ⋅ a 1 v 1 ⋅ a 1 w 1 ⋅ a 1 ] = [ a u a v a w ] . {\displaystyle {\mathbf {a}}}_{2}={\mathbf {a}}_{1}{\mathbf {R}}={\begin{bmatrix}a_{x}&a_{y}}&a_{z}\end{bmatrix}}{\begin{bmatrix}u_{x}&v_{x}&w_{x}\\u_{y}&v_{y}&w_{y}\\u_{z}&v_{z}&w_{z}\end{bmatrix}}}={\begin{bmatrix}{\mathbf {u}}_{1}\cdot {\mathbf {a}}_{1}&{\mathbf {v}}}_{1}\cdot {\mathbf {a}}_{1}&{\mathbf {w}}_{1}\cdot {\mathbf {a}}_{1}\end{bmatrix}}={\begin{bmatrix}a_{u}&a_{v}&a_{w}\end{bmatrix}}. }

A - B = |A| |B| cos(θ). |A| cos(θ) er den skalare projektion af A på B.

Fysik

I fysik er størrelsen en skalar i fysisk forstand, dvs. en fysisk størrelse uafhængig af koordinatsystemet, der udtrykkes som produktet af en numerisk værdi og en fysisk enhed, ikke blot et tal. Punktproduktet er også en skalar i denne forstand, givet ved formlen, uafhængigt af koordinatsystemet. Eksempel:

• Mekanisk arbejde er prikproduktet af kraft- og forskydningsvektorer.
• Magnetisk flux er prikproduktet af magnetfeltet og arealvektorerne.
• Volumenstrømmen er prikproduktet af væskehastigheden og arealvektorerne.

Egenskaber

Følgende egenskaber gælder, hvis a, b og c er reelle vektorer, og r er en skalar.

Punktproduktet er kommutativt:

a ⋅ b = b ⋅ a . {\displaystyle \mathbf {a} \cdot \mathbf {b} =\mathbf {b} \cdot \mathbf {a} . }

Punktproduktet er distributivt over vektoraddition:

a ⋅ ( b + c ) = a ⋅ b + a ⋅ c . {\displaystyle \mathbf {a} \cdot (\mathbf {b} +\mathbf {c} )=\mathbf {a} \cdot \mathbf {b} +\mathbf {a} \cdot \mathbf {c} . }

Punktproduktet er bilineært:

a ⋅ ( r b + c ) = r ( a ⋅ b ) + ( a ⋅ c ) . {\displaystyle \mathbf {a} \cdot (r\mathbf {b} +\mathbf {c} )=r(\mathbf {a} \cdot \mathbf {b} )+(\mathbf {a} \cdot \mathbf {c} ). }

Når det multipliceres med en skalarværdi, opfylder punktproduktet:

( c 1 a ) ⋅ ( c 2 b ) = ( c 1 c 2 ) ( a ⋅ b ) {\displaystyle (c_{1}\mathbf {a} )\cdot (c_{2}\mathbf {b} )=(c_{1}c_{2})(\mathbf {a} \cdot \mathbf {b} )}

(de to sidste egenskaber følger af de to første).

To vektorer a og b, der ikke er nul, er vinkelrette, hvis og kun hvis a - b = 0.

I modsætning til multiplikation af almindelige tal, hvor hvis ab = ac, så er b altid lig med c, medmindre a er nul, følger punktproduktet ikke annulleringsloven:

Hvis a - b = a - c og a ≠ 0, så kan vi skrive: a - (b - c) = 0 ved distributivloven; resultatet ovenfor siger, at dette blot betyder, at a er vinkelret på (b - c), hvilket stadig tillader (b - c) ≠ 0, og derfor b ≠ c.

Forudsat at basen er ortonormal, er prikproduktet invariant under isometriske ændringer af basen: rotationer, refleksioner og kombinationer, idet oprindelsen holdes fast. Ovennævnte geometriske fortolkning er baseret på denne egenskab. Med andre ord er punktproduktet for et ortonormalt rum med et vilkårligt antal dimensioner invariant under en koordinattransformation baseret på en ortogonal matrix. Dette svarer til følgende to betingelser:

• Det nye grundlag er igen ortonormalt (dvs. det er ortonormalt udtrykt i det gamle grundlag).
• De nye basisvektorer har samme længde som de gamle (dvs. enhedslængde i forhold til den gamle basis).

Hvis a og b er funktioner, er den afledte af a - b a' - b + a - b'

Tredobbelt produktudvidelse

Dette er en meget nyttig identitet (også kendt som Lagranges formel), der involverer punkt- og krydsprodukterne. Den skrives som

a × ( b × c ) = b ( a ⋅ c ) - c ( a ⋅ b ) {\displaystyle \mathbf {a} \times (\mathbf {b} \times \mathbf {c} )=\mathbf {b} (\mathbf {a} \cdot \mathbf {c} )-\mathbf {c} (\mathbf {a} \cdot \mathbf {b} )}

som er lettere at huske som "BAC minus CAB", idet man skal huske, hvilke vektorer der er prikket sammen. Denne formel bruges ofte til at forenkle vektorberegninger i fysik.

Bevis for den geometriske fortolkning

Overvej elementet i R ⁿ

v = v 1 e ^ 1 + v 2 e ^ 2 + . . . + v n e ^ n . {\displaystyle \mathbf {v} =v_{1}\mathbf {\hat {e}} _{1}+v_{2}\mathbf {\hat {e}}} _{2}+...+v_{n}\mathbf {\hat {e}} _{n}.\,}

Gentagen anvendelse af Pythagoras sætning giver for længden |v|

| v | 2 = v 1 2 + v 2 2 2 + . . . + v n 2 . {\displaystyle |\mathbf {v} |^{2}=v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2}.\,}

Men det er det samme som

v ⋅ v = v 1 2 + v 2 2 2 + . . . + v n 2 2 , {\displaystyle \mathbf {v} \cdot \mathbf {v} =v_{1}^{2}+v_{2}^{2}+v_{2}^{2}+...+v_{n}^{2},\,}

Vi kan derfor konkludere, at hvis man tager prikproduktet af en vektor v med sig selv, får man vektorens længde i kvadrat.

Lemma 1

v ⋅ v = | v | 2 . {\displaystyle \mathbf {v} \cdot \mathbf {v} =|\mathbf {v} |^{2}.\,}

Betragt nu to vektorer a og b, der udgår fra oprindelsen og er adskilt af en vinkel θ. En tredje vektor c kan defineres som

c = d e f a - b . {\displaystyle \mathbf {c} \ {\stackrel {\mathrm {def} }{=}}}\\ \mathbf {a} -\mathbf {b} .\,}

hvilket giver en trekant med siderne a, b og c. I henhold til cosinusloven har vi

| c | 2 = | a | 2 + | b | 2 - 2 | a | | b | cos θ . {\displaystyle |\mathbf {c} |^{2}=|\mathbf {a} |^{2}+|\mathbf {b} |^{2}-2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,}

Ved at erstatte de kvadrerede længder med punktprodukter i henhold til Lemma 1 får vi

c ⋅ c = a ⋅ a + b ⋅ b - 2 | a | | | b | cos θ . {\displaystyle \mathbf {c} \cdot \mathbf {c} =\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,} (1)

Men da c ≡ a - b, har vi også

c ⋅ c = ( a - b ) ⋅ ( a - b ) {\displaystyle \mathbf {c} \cdot \mathbf {c} =(\mathbf {a} -\mathbf {b} )\cdot (\mathbf {a} -\mathbf {b} )\,} ,

som i henhold til fordelingsloven udvider sig til

c ⋅ c = a ⋅ a + b ⋅ b - 2 ( a ⋅ b ) . {\displaystyle \mathbf {c} \cdot \mathbf {c} =\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2(\mathbf {a} \cdot \mathbf {b} ).\,} (2)

Ved at samle de to c - c ligninger, (1) og (2), får vi

a ⋅ a + b ⋅ b - 2 ( a ⋅ b ) = a ⋅ a + b ⋅ b - 2 | a | | | b | cos θ . {\displaystyle \mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2(\mathbf {a} \cdot \mathbf {b} )=\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,}

Hvis man trækker a - a + b - b fra begge sider og dividerer med -2, får man

a ⋅ b = | a | | b | cos θ . {\displaystyle \mathbf {a} \cdot \mathbf {b} =|\mathbf {a} ||\mathbf {b} |\cos \theta .\,}

Q.E.D.

Generalisering

Det indre produkt generaliserer prikproduktet til abstrakte vektorrum og er normalt angivet ved ⟨ a , b ⟩ {\displaystyle \langle \mathbf {a} \,,\mathbf {b} \rangle } . På grund af den geometriske fortolkning af prikproduktet er normen ||a||| for en vektor a i et sådant indre produktrum defineret som

‖ a ‖ = ⟨ a , a ⟩ {\displaystyle \|\mathbf {a} \|={\sqrt {\langle \mathbf {a} \,,\mathbf {a} \rangle }}}

således at den generaliserer længden, og vinklen θ mellem to vektorer a og b ved

cos θ = ⟨ a , b ⟩ ‖ a ‖ ‖ ‖ b ‖ . {\displaystyle \cos {\theta }={\frac {\langle \mathbf {a} \,,\mathbf {b} \rangle }{\\|\\mathbf {a} \|\|,\|\\mathbf {b} \|}}. }

To vektorer betragtes som ortogonale, hvis deres indre produkt er nul.

⟨ a , b ⟩ = 0. {\displaystyle \langle \mathbf {a} \,,\mathbf {b} \rangle =0.}

For vektorer med komplekse indgange ville den givne definition af prikproduktet føre til helt andre geometriske egenskaber. F.eks. kan en vektors prikprodukt med sig selv være et vilkårligt komplekst tal og kan være nul, uden at vektoren er nulvektor; dette ville igen have alvorlige konsekvenser for begreber som længde og vinkel. Mange geometriske egenskaber kan reddes, på bekostning af at opgive de symmetriske og bilineære egenskaber ved skalarproduktet, ved alternativt at definere

a ⋅ b = ∑ a i b i ¯ {\displaystyle \mathbf {a} \cdot \mathbf {b} =\sum {a_{i}{\overline {b_{i}}}}}

hvor b_i er det komplekse konjugat af b_i . Så skalarproduktet af enhver vektor med sig selv er et ikke-negativt reelt tal, og det er ikke nul, undtagen for nulvektoren. Dette skalarprodukt er imidlertid ikke lineært i b (men snarere konjugeret lineært), og skalarproduktet er heller ikke symmetrisk, da

a ⋅ b = b ⋅ a ¯ {\\displaystyle \mathbf {a} \cdot \mathbf {b} ={\overline {\mathbf {b} \cdot \mathbf {a} }}}} .

Denne type skalarprodukt er ikke desto mindre ganske nyttig og fører til begreberne hermitisk form og generelle indre produktrum.

Det indre Frobenius-produkt generaliserer prikproduktet til matricer. Det er defineret som summen af produkterne af de tilsvarende komponenter af to matricer af samme størrelse.

Generalisering til tensorer

Punktproduktet mellem en tensor af orden n og en tensor af orden m er en tensor af orden n+m-2. Punktproduktet beregnes ved at multiplicere og summere over et enkelt indeks i begge tensorer. Hvis A {\displaystyle \mathbf {A} } og B {\displaystyle \mathbf {B} } er to tensorer med elementrepræsentation A i j ... k ℓ ... {\displaystyle A_{ij\dots }^{k\ell \dots }} og B m n ... p ... i {\displaystyle B_{mn\dots }^{p{\dots }i}}} er elementerne i punktproduktet A ⋅ B {\displaystyle \mathbf {A} \cdot \mathbf {B} } er givet ved

A i j ... k ℓ ... B m n ... p ... i = ∑ i = 1 n A i j ... k ... k ℓ ... B m n ... p ... i {\displaystyle A_{ij\dots }^{k\ell \dots }B_{mn\dots }^{p{\dots }i}=\sum _{i=1}^{n}A_{ij\dots }^{k\ell \dots }B_{mn\dots }^{p{\dots }i}}

Denne definition kan naturligvis reduceres til det almindelige vektorpunktprodukt, når det anvendes på vektorer, og til matrixmultiplikation, når det anvendes på matricer.

Lejlighedsvis bruges et dobbelt punktprodukt til at repræsentere multiplikation og summering på tværs af to indekser. Det dobbelte punktprodukt mellem to tensorer af 2. orden er et skalarprodukt.

Relaterede sider

• Cauchy-Schwarz-ulighed
• Krydsende produkt
• Matrixmultiplikation
• Fysik