Hvad er dimensioner? Definition, typer og eksempler (1D–4D)
Lær hvad dimensioner er — definition, typer og klare eksempler fra 1D til 4D. Forstå rum, vektorrum, frihedsgrader og tid forklaret enkelt og visuelt.
Dimensioner er den måde, vi beskriver, måler og oplever verden på — både i daglig tale og i matematik og fysik. I almindelighed tænker vi på dimensioner som retninger eller frihedsgrader: op–ned, højre–venstre, frem–tilbage, men begrebet rækker videre og kan også omfatte størrelser som varmt og koldt, hvor længt noget er, hvor tungt det er, og mere abstrakte begreber fra matematik og fysik. En nyttig måde at definere en dimension på er som antallet af frihedsgrader — altså hvor mange uafhængige måder et objekt kan bevæge sig eller beskrives på i et givet rum. Begrebet bruges i flere sammenhænge, og der findes derfor forskellige definitioner, afhængig af om man taler om geometri, algebra, fysik eller topologi.
Dimension i matematik: vektorrum og basis
I et vektorrum 
vektorerne er "pile" med retninger) er dimensionen af , også skrevet som 
, lig med kardinaliteten (antallet af vektorer) i en basis af . En basis er et sæt uafhængige vektorer, der kan kombineres lineært for at danne alle vektorer i rummet — derfor angiver antallet af basisvektorer, hvor mange uafhængige retninger rummet har.
Rumlige dimensioner: 1D, 2D og 3D
De fleste genstande i vores hverdag beskrives med tre rumlige dimensioner, som ofte kaldes længde, bredde og dybde. Matematikere kalder dette et euklidisk rum. Her er nogle konkrete eksempler:
- 1D (éndimensionelt): En linje eller kurve. Et punkt på linjen kan beskrives med én koordinat (fx x). Frihedsgrader: 1.
- 2D (todimensionelt): Et plan som et stykke papir eller en skærm. Et punkt beskrives med to koordinater (x, y). Eksempler: kort, tegninger, billeder.
- 3D (tredimensionelt): Rummet omkring os — objekter med højde, bredde og dybde. Et punkt beskrives med (x, y, z). De fleste fysiske objekter har tre rumlige frihedsgrader.
4D og mere: tid, rumtid og abstrakte rum
I fysikken tilføjes ofte en fjerde dimension, 4D, nemlig tid. Når man kombinerer tid og rum, ender man med en fire-dimensionel model kaldet rumtid, hvor en begivenheds placering angives ved både sted og tidspunkt. I relativitetsteorien er dette den naturlige måde at beskrive hændelser på, fordi tid og rum er tæt forbundne og kan påvirkes af bevægelse og tyngdekraft.
Udover 4D findes i matematikken og fysikken også rum med vilkårligt mange dimensioner: f.eks. tilstandsrum i mekanik, funktionsrum i analyse eller højdimensionelle vektorrum i datalogi og statistik.
Andre betydninger af "dimension"
Begrebet bruges også i andre sammenhænge:
- Fysiske enheds-dimensioner: I fysik taler man om dimensioner som længde (L), tid (T), masse (M), elektrisk strøm (I), temperatur (varme), stofmængde og lysstyrke — disse bestemmer enhederne i fysiske ligninger (SI-systemet).
- Topologisk og fraktal dimension: Dimension kan være et mål for kompleksitet. En fraktal kan have ikke-hele (fraktal) dimension målt fx via Hausdorff-dimension, hvilket beskriver, hvordan et objekts mål skalerer med længdeskalaen.
- Praktisk brug: I teknik og statistisk analyse beskrives data ofte som punkter i et højdimensionelt rum (fx et datasæt med mange variable), hvor hver variabel er en "dimension".
Position, måling og frihedsgrader
Dimensioner bruges til at angive position: Afstanden til et punkt måles i koordinatrumets komponenter — i rumlige tilfælde i længde, bredde og højde. Antallet af uafhængige koordinater svarer til antallet af frihedsgrader og dermed til dimensionen. Hvis et objekt er bundet af en begrænsning (fx er fastgjort til en skinnesnor), reduceres dets frihedsgrader, og dermed den effektive dimension, der beskriver dets bevægelse.
Korte, konkrete eksempler
- En bil, der kører langs en vej: bevægelsen kan beskrives som 1D langs vejens længde.
- En robotarm i et plan: positionen af armens ende beskrives i 2D.
- Et æble i rummet: position i 3D (x, y, z).
- En begivenhed (fx et lynnedslag): kræver 3 rumlige koordinater + 1 tid, altså 4D for fuld beskrivelse.
Sammenfattende kan man sige, at "dimension" altid handler om, hvor mange uafhængige tal eller retninger der er nødvendige for at beskrive noget fuldstændigt — hvad enten det er en linje, et fysisk system, et abstrakt vektorrum eller en temperaturmåling. Valget af definition afhænger af den konkrete anvendelse: geomtri, algebra, fysik eller dataanalyse.
Et diagram over de første fire rumlige dimensioner.
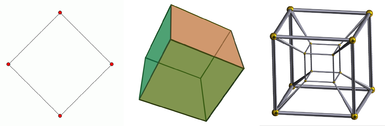
Fra venstre til højre: kvadratet, terningen og tesseraktet. Firkanten er et 2-dimensionelt objekt, terningen er et 3-dimensionelt objekt, og tesseraktet er et 4-dimensionelt objekt. Et 1-dimensionelt objekt er blot en linje. Der gives en projektion af terningen, da den ses på en todimensional skærm. Det samme gælder for tesseraktet, som desuden kun kan vises som en projektion, selv i et tredimensionelt rum.
Andre dimensioner
I den moderne videnskab bruger man andre dimensioner. Dimensioner som temperatur og vægt kan bruges til at vise, hvor noget befinder sig i mindre enkle rum. Forskere studerer disse dimensioner med dimensionsanalyse.
Matematikere bruger også dimensioner. I matematikken er dimensioner mere generelle. Dimensioner i matematik måler måske ikke ting i verden. Reglerne for aritmetik med dimensioner i matematik kan være anderledes end de sædvanlige aritmetiske regler.
Dimensioner og vektorer
Vektorer bruges til at vise afstande og retninger. Vektorer bruges ofte inden for teknik og videnskab og nogle gange også i matematik.
En vektor er en liste af tal. Der er et tal for hver dimension. Der findes aritmetiske regler for vektorer.
Hvis Jane f.eks. ønsker at kende Sally's position, kan Sally give Jane en vektor, der viser positionen. Hvis Jane og Sally befinder sig i verden, er der tre dimensioner. Derfor giver Sally Jane en liste med tre tal for at vise hendes position. De tre tal i den vektor, som Sally giver Jane, kan være følgende:
- Sally's afstand nord for Jane
- Sallys afstand øst for Jane
- Sally's højde over Jane
Relaterede sider
- 3D
- Hypercube, generalisering af kvadrat og terning ud over tre dimensioner
- Minkowski rumtid, en fire-dimensionel mangfoldighed
- Rum-tid
Spørgsmål og svar
Q: Hvad er en dimension?
A: En dimension er en måde at måle, se og opleve verden på ved hjælp af begreber som op og ned, fra højre til venstre, fra ryg til front, fra varmt til koldt, hvor tungt og hvor langt. Det kan også defineres som frihedsgrader eller den måde, et objekt kan bevæge sig på i et bestemt rum.
Spørgsmål: Hvordan definerer matematikere det euklidiske rum?
A: Matematikere definerer det euklidiske rum som værende specificeret af tre dimensioner, der normalt kaldes længde, bredde og dybde.
Spørgsmål: Hvad er antallet af vektorer i et vektorrum?
Svar: Antallet af vektorer i et vektorrum er lig med kardinaliteten (eller antallet af vektorer) af dets basissæt.
Spørgsmål: Hvor mange dimensioner anvendes til at måle position?
Svar: Der anvendes tre dimensioner (længde, bredde og højde) til at måle position. I nogle tilfælde kan der anvendes en fjerde (4D) dimension - tid - til at vise en begivenheds position i tid og rum.
Spørgsmål: Hvad betyder dim(V)?
A: Dim(V) henviser til dimensionen af V, som er lig med kardinaliteten (eller antallet af vektorer) af dens basissæt eller lig med antallet af retlinieretninger, som den har.
Spørgsmål: Er der én definition, der opfylder alle begreber i forbindelse med dimensioner?
Svar: Nej, der findes ikke en enkelt definition, der kan opfylde alle begreber i forbindelse med dimensioner.
Søge