Magnetisk moment (dipolmoment): Hvad er det? Definition og eksempler
Forstå magnetisk moment (dipolmoment): klar definition, fysiske principper og konkrete eksempler på magneter, strømme, partikler og molekyler.
Magnetens magnetiske moment er en størrelse, der bestemmer den kraft, som magneten kan udøve på elektriske strømme, og det moment, som et magnetfelt vil udøve på den. En elektrisk strømsløjfe, en stangmagnet, en elektron, et molekyle og en planet har alle et magnetisk moment.
Både det magnetiske moment og det magnetiske felt kan betragtes som vektorer med en størrelse og en retning. Retningen af det magnetiske moment peger fra en magnetens syd- til nordpol. Det magnetiske felt, som en magnet frembringer, er også proportionalt med dens magnetiske moment. Mere præcist henviser udtrykket magnetisk moment normalt til et systems magnetiske dipolmoment, som giver det første udtryk i multipoludvidelsen af et generelt magnetfelt. Dipolkomponenten af et objekts magnetfelt er symmetrisk omkring det magnetiske dipolmoment og aftager som den omvendte terning af afstanden fra objektet.
Definition og formler
Det magnetiske dipolmoment betegnes ofte med symbolet μ og måles i SI-enheden A·m² (ampere gange kvadratmeter), som også kan skrives som joule per tesla (J/T). Nogle nyttige formler:
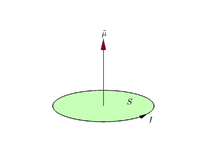
- For en flad sløjfe med strøm: μ = I·A·n, hvor I er strømmen, A er sløjfens areal og n er normalvektoren (retningen givet af højre-håndsregel).
- For en spole med N viklinger: μ = N·I·A.
- For et roterende ladet partikel (orbitalt moment): μ = (q/2m)·L, hvor q er ladningen, m massen og L det mekaniske vinkelmoment. For spindmoment indgår ofte en g-faktor, så μ = g (q/2m) S.
- Potentiel energi af en dipol i et eksternt felt: U = −μ · B.
- Drejningsmoment på en dipol i et felt: τ = μ × B (giver tendens til at dreje dipolen, så μ kommer i samme retning som B).
Retning: højre-håndsregel og poler
Retningen af μ kan bestemmes ved højre-håndsreglen: hvis fingrene følger strømmens retning i en sløjfe, peger tommelfingeren i retningen af μ (og dermed mod nordpolen på magneten). For atomare partikler svarer retningen til deres samlede magnetiske moment fra spin og orbital bevægelse.
Magnetfelt fra en dipol
Det magnetiske felt langt fra en dipol kan tilnærmes af dipolfeltet. På vektornedskrevet form for et punkt i afstand r fra dipolen er
B(r) = (μ0 / 4π r³) [3(μ · r̂) r̂ − μ],
hvor μ0 er vakuumpermeabiliteten og r̂ er enhedsvektoren i r- retningen. På dipolens akse (θ = 0) forenkles udtrykket til
B = (μ0 / 4π) · (2μ / r³).
Bemærk at feltet falder som 1/r³, hvilket betyder, at dipolkomponenten dominerer langt fra kilden, men bliver hurtigt svagere med afstand.
Eksempler og størrelsesordener
- En simpel strømførende loop: en kvadratisk sløjfe med side 0,1 m og strøm I = 1 A har μ = I·A = 1·(0,1·0,1) = 0,01 A·m².
- Elektronens magnetiske moment (på grund af spin) har størrelsesordenen Bohr-magnetonen: μB ≈ 9,274×10⁻²⁴ J/T.
- Jordens magnetiske dipolmoment er cirka 8×10²² A·m² (stort tal — derfor kan Jorden påvirke kompasser over meget store afstande).
Måling og anvendelser
Magnetiske momenter måles med forskellige teknikker, fx:
- Magnetometre (fluxgate, SQUID) til bestemmelser af store og små magnetmomenter.
- Stern–Gerlach-eksperimentet, som adskiller partikler efter deres magnetiske moment (kvantemåling).
- Drejningsmoment-magnetometri, hvor man måler den vinkel eller kraft et felt udøver på et prøvemateriale.
Anvendelser hvor forståelse af magnetisk moment er central: kompas og navigation, elmotorer, generatorer, magnetisk dataopbevaring, MRI-billeddannelse og grundforskning i atom- og materialevidenskab.
Bemærkninger og forskel til elektrisk dipolmoment
Det magnetiske dipolmoment er forskelligt fra det elektriske dipolmoment: et elektrisk dipolmomet beskriver separation af positive og negative ladninger og skaber elektriske felter, mens det magnetiske dipolmomet opstår fra bevægelser af ladninger (strømme) eller partikelspins og skaber magnetfelter. I mange materialer kan microskopiske magnetiske momenter addere sig og give en makroskopisk magnetisering (magnetic moment per volumen).
Samlet set er det magnetiske dipolmoment et centralt begreb i både klassisk og kvantemekanisk beskrivelse af magnetisme: det bestemmer feltet langt fra kilden, hvordan kilden interagerer med eksterne magnetfelter (drejningsmoment og energi), og hvordan materialer og partikler reagerer i magnetiske miljøer.
To definitioner af moment
I lærebøgerne anvendes to komplementære metoder til at definere magnetiske momenter. I lærebøger fra før 1930'erne blev de defineret ved hjælp af magnetiske poler. De fleste nyere lærebøger definerer dem ved hjælp af ampèriske strømme.
Definition af magnetisk pol
Fysikere fremstiller kilder til magnetiske momenter i materialer som poler. Nord- og sydpolerne er en analogi til de positive og negative ladninger i elektrostatikken. Tænk på en stangmagnet, som har magnetiske poler af samme størrelse, men med modsat polaritet. Hver pol er kilde til en magnetisk kraft, som svækkes med afstanden. Da de magnetiske poler altid er parvis, ophæver deres kræfter delvist hinanden, fordi den ene pol trækker, mens den anden frastøder. Denne ophævelse er størst, når polerne er tæt på hinanden, dvs. når stangmagneten er kort. Den magnetiske kraft, som en stangmagnet frembringer i et givet punkt i rummet, afhænger derfor af to faktorer: af både polernes styrke p {\displaystyle p}

m = p l . {\displaystyle \mathbf {m} =p\mathbf {l} . }
Den peger i retning fra syd til nordpolen. Analogien med elektriske dipoler bør ikke gå for vidt, da magnetiske dipoler er forbundet med vinkelmoment (se Magnetisk moment og vinkelmoment). Ikke desto mindre er magnetiske poler meget nyttige i magnetostatiske beregninger, især i forbindelse med ferromagneter. Praktikere, der anvender den magnetiske poltilgang, repræsenterer generelt det magnetiske felt ved hjælp af det irroterende felt H {\displaystyle \mathbf {H} } 

Definition af strømkredsløbet
Lad os antage, at en plan lukket sløjfe fører en elektrisk strøm I {\displaystyle I}








m = I S . {\displaystyle \mathbf {m} =I\mathbf {S} . }
Konventionelt er retningen af vektorområdet givet ved hjælp af reglen om højrehåndsgreb (man krøller højre hånds fingre i strømretningen rundt om løkken, når håndfladen "rører" løkkens yderkant, og den lige tommelfinger angiver retningen af vektorområdet og dermed det magnetiske moment).
Hvis løkken ikke er plan, er momentet givet som
m = I2 ∫ r × d r . {\displaystyle \mathbf {m} ={\frac {I}{2}}}\int \mathbf {r} \times {\rm {\rm {d}}}\mathbf {r} . }
I det mest generelle tilfælde med en vilkårlig strømfordeling i rummet kan det magnetiske moment for en sådan fordeling findes ud fra følgende ligning:
m = 12∫ r × J d V , {\displaystyle \mathbf {m} ={\frac {1}{2}}}\int \mathbf {r} \times \mathbf {J} \,{\rm {d}}}V,}
hvor r {\displaystyle \mathbf {r} }

Ovenstående ligning kan bruges til at beregne det magnetiske moment af en hvilken som helst samling af bevægelige ladninger, f.eks. et roterende ladet fast stof, ved at erstatte
J = ρ v , {\displaystyle \mathbf {J} =\rho \mathbf {v} ,}
hvor ρ {\displaystyle \rho }

F.eks. er det magnetiske moment, der frembringes af en elektrisk ladning, der bevæger sig langs en cirkulær bane, følgende
m = q 12r × v {\displaystyle \mathbf {m} ={\frac {1}{2}}}\,q\,q\,\mathbf {r} \times \mathbf {v} } } 
hvor r {\displaystyle \mathbf {r} }


Praktikere, der anvender strømsløjfe-modellen, repræsenterer generelt det magnetiske felt ved hjælp af det solenoidale felt B {\displaystyle \mathbf {B} } 

Magnetisk moment i en solenoide
En generalisering af ovenstående strømsløjfe er en multi-turn spole eller solenoide. Dens moment er vektorsummen af momenterne for de enkelte vindinger. Hvis solenoiden har N {\displaystyle N} 
m = N I S . {\displaystyle \mathbf {m} =NI\mathbf {S} . }
.svg.png)
3D-billede af en magnetventil.
Moment m {\displaystyle \mathbf {m} }


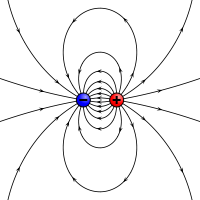
En elektrostatisk analog til et magnetisk moment: to modsatrettede ladninger adskilt af en finite afstand.
Enheder
Enheden for magnetisk moment er ikke en basisenhed i det internationale enhedssystem (SI), og den kan repræsenteres på mere end én måde. I definitionen af strømsløjfen måles arealet f.eks. i kvadratmeter, og I {\displaystyle I}


A m = 2N.m T -1 . {\displaystyle \,{\text{A m}}}^{2}=\,{\text{N.m T}}^{-1}. }
I CGS-systemet findes der flere forskellige sæt elektromagnetiske enheder, hvoraf de vigtigste er ESU, Gaussian og EMU. Blandt disse er der to alternative (ikke-ækvivalente) enheder for det magnetiske dipolmoment i CGS:
(ESU CGS) 1 statA-cm² = 3,33564095×10-14 (m-A2 eller N.m/T)
og (hyppigere anvendt)
(EMU CGS og Gaussian-CGS) 1 erg/G = 1 abA-cm² = 10-3 (m-A2 eller N.m/T).
Forholdet mellem disse to ikke-ækvivalente CGS-enheder (EMU/ESU) er nøjagtigt lig med lysets hastighed i det frie rum, udtrykt i cm/s.
Alle formler i denne artikel er korrekte i SI-enheder, men i andre enhedssystemer kan det være nødvendigt at ændre formlerne i andre enhedssystemer. I SI-enheder har f.eks. en strømsløjfe med strømmen I og arealet A et magnetisk moment I×A (se nedenfor), men i Gauss-enheder er det magnetiske moment I×A/c.
| Intrinsiske magnetiske momenter og spins hos nogle elementarpartikler | ||
| Partikel | Magnetisk dipolmoment i SI-enheder (10 −27J/T) | Spinkvantetal (dimensionsløst) |
| -9284.764 | 1/2 | |
| proton | 14.106067 | 1/2 |
| neutron | -9.66236 | 1/2 |
| myon | -44.904478 | 1/2 |
| deuteron | 4.3307346 | 1 |
| triton | 15.046094 | 1/2 |
For forholdet mellem begreberne magnetisk moment og magnetisering, se magnetisering.
Spørgsmål og svar
Q: Hvad er det magnetiske moment for en magnet?
A: En magnets magnetiske moment er en størrelse, der bestemmer den kraft, som magneten kan udøve på elektriske strømme, og det drejningsmoment, som et magnetfelt vil udøve på den.
Q: Hvilke objekter har magnetiske momenter?
A: En sløjfe af elektrisk strøm, en stangmagnet, en elektron, et molekyle og en planet har alle magnetiske momenter.
Q: Hvordan kan man betragte både det magnetiske moment og det magnetiske felt?
A: Både det magnetiske moment og magnetfeltet kan betragtes som vektorer, der har en størrelse og en retning.
Q: Hvilken retning peger det magnetiske moment i en magnet?
A: Retningen af det magnetiske moment peger fra sydpolen til nordpolen på en magnet.
Q: Hvad er forholdet mellem det magnetiske moment og magnetfeltet i en magnet?
A: Det magnetiske felt, der produceres af en magnet, er proportionalt med dens magnetiske moment.
Q: Hvad refererer udtrykket magnetisk moment normalt til?
A: Mere præcist refererer udtrykket magnetisk moment normalt til et systems magnetiske dipolmoment, som producerer det første udtryk i multipoludvidelsen af et generelt magnetfelt.
Q: Hvordan opfører dipolkomponenten i et objekts magnetfelt sig, når afstanden fra objektet øges?
A: Dipolkomponenten i et objekts magnetfelt er symmetrisk omkring retningen af dets magnetiske dipolmoment og aftager som den inverse terning af afstanden fra objektet.
Søge