Harmonisk række

Historie

Det faktum, at den harmoniske serie divergerer, blev først bevist i det 14. århundrede af Nicole Oresme, men blev glemt. Beviserne blev givet i det 17. århundrede af Pietro Mengoli, Johann Bernoulli og Jacob Bernoulli.

Harmoniske sekvenser er blevet anvendt af arkitekter. I baroktiden brugte arkitekter dem i proportionerne i grundplaner, elevationer og i forholdet mellem arkitektoniske detaljer i kirker og paladser.

 

Divergens

Der findes flere velkendte beviser for divergensen af den harmoniske serie. Et par af dem er angivet nedenfor.

Sammenligningstest

En måde at bevise divergens på er at sammenligne den harmoniske serie med en anden divergent serie, hvor hver nævner er erstattet med den næststørste potens af to:

1 + 1 2 + 1 3 + 1 4 + 1 5 + 1 6 + 1 6 + 1 7 + 1 8 + 1 9 + ⋯ ≥ 1 + 1 2 + 1 4 + 1 4 + 1 4 + 1 8 + 1 8 + 1 8 + 1 8 + 1 8 + 1 8 + 1 8 + 1 16 + ⋯ {\displaystyle {\begin{aligned}&{}1+{\frac {1}{2}}}+{\frac {1}{3}}}+{\frac {1}{4}}}+{\frac {1}{5}}}+{\frac {1}{6}}}+{\frac {1}{7}}}+{\frac {1}{8}}}+{\frac {1}{9}}}+\cdots \\[12pt]\geq {}&1+{\frac {1}{2}}}+{\frac {1}{\color {red}{\mathbf {4} }}}+{\frac {1}{4}}}+{\frac {1}{\color {red}{\mathbf {8} }}}+{\frac {1}{{\color {red}{\mathbf {8} }}}+{\frac {1}{{\color {red}{\mathbf {8}} }}}+{\frac {1}{8}}}+{\frac {1}{\color {red}{\mathbf {16} }}}+\cdots \end{aligned}}}}

Hver term i den harmoniske serie er større end eller lig med den tilsvarende term i den anden serie, og derfor må summen af den harmoniske serie være større end eller lig med summen af den anden serie. Summen af den anden serie er imidlertid uendelig:

1 + ( 1 2 ) + ( 1 4 + 1 4 ) + ( 1 8 + 1 8 + 1 8 + 1 8 + 1 8 ) + ( 1 16 + ⋯ + 1 16 ) + ⋯ = 1 + 1 2 + 1 2 + 1 2 + 1 2 + 1 2 + 1 2 + ⋯ = ∞ {\displaystyle {\begin{aligned}&{}1+\left({\frac {1}{2}}}\right)+\left({\frac {1}{4}}}\!+\!{\frac {1}{4}}}\right)+\left({\frac {1}{8}}}\!+\!{\frac {1}{8}}}\!+\!{\frac {1}{8}}}\!+\!{\frac {1}{8}}}}\right)+\left({\frac {1}{16}}}}\!+\!\cdots \!+\!{\frac {1}{16}}}\right)+\cdots \\[12pt]={}&1+{\frac {1}{2}}}+{\frac {1}{2}}}+{\frac {1}{2}}}+{\frac {1}{2}}}+{\frac {1}{2}}+\cdots =\infty \end{aligned}}}

Heraf følger (ved sammenligningstesten), at summen af de harmoniske serier også må være uendelig. Mere præcist beviser ovenstående sammenligning, at

∑ n = 1 2 k 1 1 n ≥ 1 + k 2 {\displaystyle \sum _{n=1}^{2^{k}}}{\frac {1}{n}}{n}}\geq 1+{{\frac {k}{2}}}}

for hvert positivt heltal k.

Dette bevis, som blev foreslået af Nicole Oresme omkring 1350, anses for at være et højdepunkt i middelalderens matematik. Det er stadig et standardbevis, der undervises i matematikundervisning i dag.

Integralprøve

Det er muligt at bevise, at den harmoniske serie divergerer ved at sammenligne dens sum med et ukorrekt integral. Overvej den rektangulære opstilling, der er vist i figuren til højre. Hvert rektangel er 1 enhed bredt og

1/n enheder høj, så det samlede areal af det uendelige antal rektangler er summen af de harmoniske serier:

arealet af rektangler = 1 + 1 2 + 1 3 + 1 4 + 1 4 + 1 5 + ⋯ {\displaystyle {\begin{array}{c}{\text{area of}}\\{\text{rectangles}}\{end{array}}}=1+{{\frac {1}{2}}}+{\frac {1}{3}}}+{\frac {1}{4}}}+{\frac {1}{5}}+\cdots }

Det samlede areal under kurven y =

1/x fra 1 til uendelig er givet ved et divergerende ukorrekt integral:

areal under kurven = ∫ 1 ∞ 1 x d x = ∞ . {\displaystyle {\begin{array}{c}{{\text{areal under}}}{\text{kurve}}\end{array}}}=\int _{1}^{\infty }{\frac {1}{x}}}\,dx=\infty .}

Da dette areal er helt indeholdt i rektanglerne, må det samlede areal af rektanglerne også være uendeligt. Dette beviser, at

∑ n = 1 k 1 1 n > ∫ 1 k + 1 1 1 1 x d x = ln ( k + 1 ) . {\displaystyle \sum _{n=1}^{k}{\frac {1}{n}}}>\int _{1}^{k+1}{\frac {1}{x}}}\,dx=\ln(k+1).}

Generaliseringen af dette argument er kendt som den såkaldte integralprøve.

 
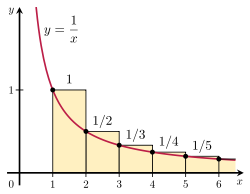
Illustration af den integrale test.  

Divergenshastighed

Den harmoniske serie divergerer meget langsomt. F.eks. er summen af de første 10 termer på⁴³ mindre end 100. Det skyldes, at seriens partielle summer har logaritmisk vækst. Især,

∑ n = 1 k 1 n = ln k + γ + ε k ≤ ( ln k ) + 1 {\displaystyle \sum _{n=1}^{k}{\frac {1}{n}}}=\ln k+\gamma +\varepsilon _{k}\leq (\ln k)+1}

hvor γ er Euler-Mascheroni-konstanten og ε_k ~

1/2k, som nærmer sig 0, når k går mod uendeligt. Leonhard Euler beviste både dette og at summen, der kun omfatter de reciprokke primtal af primtal, også divergerer, dvs:

∑ p primtal 1 p = 1 2 + 1 3 + 1 5 + 1 7 + 1 11 + 1 13 + 1 17 + ⋯ = ∞ . {\displaystyle \sum _{p{\text{ prime }}}{\frac {1}{p}}}={\frac {1}{2}}}+{\frac {1}{3}}}+{\frac {1}{5}}}+{\frac {1}{7}}+{\frac {1}{11}}+{\frac {1}{13}}+{\frac {1}{17}}+\cdots =\infty .}
 

Delvise summer

De første tredive harmoniske tal
n	Delsummen af den harmoniske serie, Hn
	udtrykt som en brøkdel		decimal	relativ størrelse
1	1		~1	1
2	3	/2	~1.5	1.5
3	11	/6	~1.83333	1.83333
4	25	/12	~2.08333	2.08333
5	137	/60	~2.28333	2.28333
6	49	/20	~2.45	2.45
7	363	/140	~2.59286	2.59286
8	761	/280	~2.71786	2.71786
9	7129	/2520	~2.82897	2.82897
10	7381	/2520	~2.92897	2.92897
11	83711	/27720	~3.01988	3.01988
12	86021	/27720	~3.10321	3.10321
13	1145993	/360360	~3.18013	3.18013
14	1171733	/360360	~3.25156	3.25156
15	1195757	/360360	~3.31823	3.31823
16	2436559	/720720	~3.38073	3.38073
17	42142223	/12252240	~3.43955	3.43955
18	14274301	/4084080	~3.49511	3.49511
19	275295799	/77597520	~3.54774	3.54774
20	55835135	/15519504	~3.59774	3.59774
21	18858053	/5173168	~3.64536	3.64536
22	19093197	/5173168	~3.69081	3.69081
23	444316699	/118982864	~3.73429	3.73429
24	1347822955	/356948592	~3.77596	3.77596
25	34052522467	/8923714800	~3.81596	3.81596
26	34395742267	/8923714800	~3.85442	3.85442
27	312536252003	/80313433200	~3.89146	3.89146
28	315404588903	/80313433200	~3.92717	3.92717
29	9227046511387	/2329089562800	~3.96165	3.96165
30	9304682830147	/2329089562800	~3.99499	3.99499

De endeløse partielle summer af divergerende harmoniske serier,

H n = ∑ k = 1 n 1 k , {\displaystyle H_{n}=\sum _{k=1}^{n}{\frac {1}{k}}},}

kaldes harmoniske tal.

Forskellen mellem H_n og ln n konvergerer mod Euler-Mascheroni-konstanten. Forskellen mellem to harmoniske tal er aldrig et helt tal. Ingen harmoniske tal er hele tal, undtagen H₁ = 1.

 

Relaterede serier

Skiftende harmoniske serier

Serien

∑ n = 1 ∞ ( - 1 ) n + 1 n = 1 - 1 2 + 1 3 - 1 4 + 1 5 - ⋯ {\displaystyle \sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}}{n}}=1-{\frac {1}{2}}}+{\frac {1}{3}}}-{\frac {1}{4}}}+{\frac {1}{5}}}-\cdots }

er kendt som den vekslende harmoniske serie. Denne serie konvergerer ved hjælp af den vekslende serietest. Især er summen lig med den naturlige logaritme af 2:

1 - 1 2 + 1 3 - 1 4 + 1 5 - ⋯ = ln 2. {\displaystyle 1-{\frac {1}{2}}}+{\frac {1}{3}}}-{\frac {1}{4}}}+{\frac {1}{5}}}-\cdots =\ln 2.}

Den vekslende harmoniske serie er, selv om den er betinget konvergent, ikke absolut konvergent: hvis termerne i serien omlægges systematisk, bliver summen generelt anderledes og, afhængigt af omlægningen, muligvis endda uendelig.

Den vekslende harmoniske serieformel er et specialtilfælde af Mercator-serien, Taylor-serien for den naturlige logaritme.

En beslægtet serie kan udledes af Taylor-serien for arktangenten:

∑ n = 0 ∞ ( - 1 ) n 2 n + 1 = 1 - 1 3 + 1 5 - 1 7 + ⋯ = π 4 . {\displaystyle \sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}}=1-{\frac {1}{3}}}+{\frac {1}{5}}}-{\frac {1}{7}}}+\cdots ={\frac {\pi }{4}}}.}

Dette er kendt som Leibniz-serien.

Generelle harmoniske serier

Den generelle harmoniske serie er af formen

∑ n = 0 ∞ 1 a n + b , {\displaystyle \sum _{n=0}^{\infty }{\frac {1}{an+b}}},}

hvor a ≠ 0 og b er reelle tal, og

b/a er ikke nul eller et negativt heltal.

Ved grænsesammenligningstesten med de harmoniske serier divergerer alle generelle harmoniske serier også.

p-serien

En generalisering af den harmoniske serie er p-serien (eller hyperharmoniske serie), defineret som

∑ n = 1 ∞ 1 n p {\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{p}}}}

for ethvert reelt tal p. Når p = 1, er p-serien den harmoniske serie, som er divergerende. Enten integralprøven eller Cauchy-kondensationsprøven viser, at p-serien konvergerer for alle p > 1 (i så fald kaldes den overharmonisk serie) og divergerer for alle p ≤ 1. Hvis p > 1, er summen af p-serierne ζ(p), dvs. Riemann-vetafunktionen evalueret ved p.

Problemet med at finde summen for p = 2 kaldes Basel-problemet; Leonhard Euler viste, at det er

π² /6. Værdien af summen for p = 3 kaldes Apérys konstant, da Roger Apéry har bevist, at det er et irrationelt tal.

ln-serien

Relateret til p-serien er ln-serien, der er defineret som

∑ n = 2 ∞ 1 n ( ln n ) p {\displaystyle \sum _{n=2}^{\infty }{\frac {1}{n(\ln n)^{p}}}}

for ethvert positivt reelt tal p. Dette kan vises ved hjælp af integralprøven, at det divergerer for p ≤ 1, men konvergerer for alle p > 1.

φ-serien

For enhver konveks, reelt værdifuld funktion φ, således at

lim sup u → 0 + φ ( u 2 ) φ ( u ) < 1 2 , {\displaystyle \limsup _{u\to 0^{+}}}{\frac {\varphi \left({\frac {u}{2}}\right)}{\varphi (u)}}<{\frac {1}{2}}},}

serien

∑ n = 1 ∞ φ ( 1 n ) {\displaystyle \sum _{n=1}^{\infty }\varphi \left({\frac {1}{n}}}}\right)}

er konvergent.

Tilfældige harmoniske serier

Den tilfældige harmoniske serie

∑ n = 1 ∞ s n n n , {\displaystyle \sum _{n=1}^{\infty }{\frac {s_{n}}}{n}},}

hvor s_n er uafhængige, identisk fordelte tilfældige variabler, der med samme sandsynlighed har værdierne +1 og -1

1/2, er et velkendt eksempel i sandsynlighedsteorien på en serie af tilfældige variabler, der konvergerer med sandsynligheden 1. Denne konvergens er en nem konsekvens af enten Kolmogorovs sætning om tre serier eller af den nært beslægtede Kolmogorovs maksimale ulighed. Byron Schmuland fra University of Alberta undersøgte yderligere egenskaberne ved den tilfældige harmoniske serie og viste, at den konvergerende serie er en tilfældig variabel med nogle interessante egenskaber. Især har sandsynlighedsdensitetsfunktionen for denne tilfældige variabel, der evalueres ved +2 eller -2, værdien 0,124999999999999999999999999999999999999999999999999999999999764 ..., hvilket afviger fra 1/8 med mindre end 10⁻⁴² . Schmulands artikel forklarer, hvorfor denne sandsynlighed er så tæt på, men ikke nøjagtigt 1/8. Den nøjagtige værdi af denne sandsynlighed er givet ved det uendelige cosinusproduktintegral C₂ divideret med π.

Udtømt harmonisk serie

Den udtømte harmoniske serie, hvor alle termer, hvor cifferet 9 forekommer et sted i nævneren, er fjernet, kan påvises at konvergere, og dens værdi er mindre end 80. Faktisk konvergerer serien, når alle termer, der indeholder en bestemt række af tal (i en hvilken som helst base), fjernes.

 
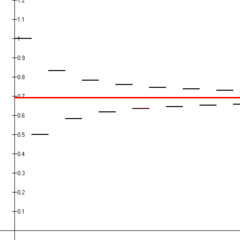
De første 14 partielle summer af den vekslende harmoniske serie (sorte linjesegmenter), der konvergerer mod den naturlige logaritme af 2 (rød linje).  

Applikationer

Den harmoniske serie kan være kontraintuitiv. Det skyldes, at det er en divergent serie, selv om seriens termer bliver mindre og går mod nul. Divergensen i den harmoniske serie er kilden til nogle paradokser.

• "Ormen på elastikken". Lad os antage, at en orm kravler langs et uendeligt elastisk 1-meter-gummibånd samtidig med, at gummibåndet strækkes ensartet. Hvis ormen bevæger sig 1 centimeter i minuttet, og båndet strækkes 1 meter i minuttet, vil ormen så nogensinde nå til enden af gummibåndet? Svaret er modsætningsvist nok "ja", for efter n minutter er forholdet mellem den afstand, som ormen tilbagelægger, og gummibåndets samlede længde

1 100 ∑ k = 1 n 1 1 k . {\displaystyle {\frac {\frac {1}{100}}}\sum _{k=1}^{n}{\frac {1}{k}}}.}

Da serien bliver vilkårligt stor, når n bliver større, må dette forhold til sidst overstige 1, hvilket betyder, at ormen når enden af gummibåndet. Den værdi af n, hvor dette sker, skal imidlertid være ekstremt stor: ca. e¹⁰⁰ , et tal, der overstiger 10⁴³ minutter (10³⁷ år). Selv om den harmoniske serie divergerer, sker det meget langsomt.

• Jeep-problemet drejer sig om, hvor meget brændstof der i alt kræves for at en bil med begrænset brændstofkapacitet kan krydse en ørken og efterlade brændstofdråber langs ruten. Den afstand, som bilen kan tilbagelægge med en given mængde brændstof, er relateret til de delvise summer af de harmoniske serier, som vokser logaritmisk. Det nødvendige brændstofbehov stiger således eksponentielt med den ønskede afstand.

• Block-stacking-problemet: Hvis man har en samling af identiske dominobrikker, er det muligt at stable dem på kanten af et bord, så de hænger over bordkanten uden at falde ned. Det kontraintuitive resultat er, at de kan stables på en sådan måde, at overhænget bliver så stort som ønsket. Det vil sige, forudsat at der er nok dominobrikker.

• En svømmer, der svømmer hurtigere, hver gang han eller hun rører svømmebassinets væg. Svømmeren begynder at krydse et 10-meter bassin med en hastighed på 2 m/s, og ved hver passage tilføjes yderligere 2 m/s til hastigheden. I teorien er svømmerens hastighed ubegrænset, men antallet af overskridelser af bassinet, der er nødvendige for at nå denne hastighed, bliver meget stort; for at nå lysets hastighed (hvis man ser bort fra den specielle relativitetsteori) skal svømmeren f.eks. krydse bassinet 150 millioner gange. I modsætning til dette store tal afhænger den tid, der er nødvendig for at nå en given hastighed, af summen af serierne ved et givet antal gennemløb af bassinet:

10 2 ∑ k = 1 n 1 1 k . {\displaystyle {\frac {\frac {10}{2}}}\sum _{k=1}^{n}{\frac {1}{k}}}.}

En beregning af summen viser, at den tid, der er nødvendig for at nå lysets hastighed, kun er 97 sekunder.

 
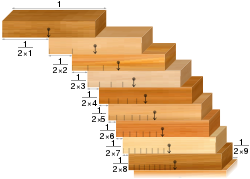
Problemet med stabling af blokke: blokke, der er opstillet i overensstemmelse med den harmoniske serie, danner broer over kløfter af vilkårlig bredde.  

Relaterede sider

• Harmonisk progression
• Liste over summen af reciprokaler