Sandsynlighedstæthedsfunktion | funktion, der karakteriserer enhver kontinuert sandsynlighedsfordeling

Inden for sandsynlighed og statistik er en sandsynlighedstæthedsfunktion en funktion, der karakteriserer enhver kontinuerlig sandsynlighedsfordeling. For en tilfældig variabel X skrives sandsynlighedsdensitetsfunktionen for X undertiden som f X ( x ) {\displaystyle f_{X}(x)} $f_{X}(x)$ . Integralet af sandsynlighedsdensitetsfunktionen i intervallet [ a , b ] {\displaystyle [a,b]} $[a,b]$ giver sandsynligheden for, at en given tilfældig variabel med den givne tæthed er indeholdt i det angivne interval. Sandsynlighedsdensitetsfunktionen er pr. definition ikke-negativ i hele sit område, hvor integralet summerer til 1.

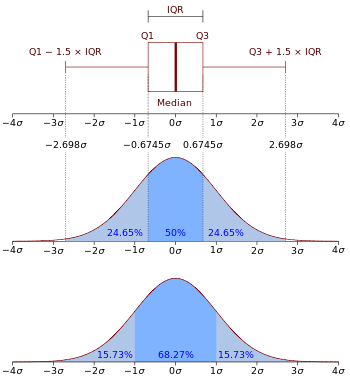
Boxplot og sandsynlighedsdensitetsfunktion for en normalfordeling N(0, σ2 ).

Sandsynlighedstæthed versus sandsynlighedsmassefunktion

Sandsynlighedsmassefunktionen er for en diskret sandsynlighedsfordeling det samme som sandsynlighedsdensitetsfunktionen er for en kontinuert sandsynlighedsfordeling. Sandsynlighedsdensitetsfunktionen er nødvendig for at kunne arbejde med kontinuerte fordelinger.

En tilfældig variabel med en kontinuert sandsynlighedsfordeling kan antage enhver værdi inden for denne fordeling. Hvis man kaster en terning, får man tallene 1 til 6 med en sandsynlighed på 1 6 {\displaystyle {\tfrac {\tfrac {1}{6}}}} ${\tfrac {1}{6}}$ , men dette er ikke en kontinuert funktion, da kun tallene 1 til 6 er mulige.

Derimod har to personer ikke samme højde eller vægt. Ved hjælp af en sandsynlighedstæthedsfunktion er det muligt at bestemme sandsynligheden for personer mellem 180 cm og 181 cm eller mellem 80 kg og 81 kg, selv om der er uendeligt mange værdier mellem disse to grænser.

Relaterede sider

Kumulativ fordelingsfunktion

Spørgsmål og svar

Spørgsmål: Hvad er en sandsynlighedstæthedsfunktion?

A: En sandsynlighedstæthedsfunktion er en funktion, der karakteriserer enhver kontinuerlig sandsynlighedsfordeling.

Spørgsmål: Hvordan skrives sandsynlighedsdensitetsfunktionen for en tilfældig variabel X?

Svar: Sandsynlighedsdensitetsfunktionen for X skrives undertiden som f_X(x).

Spørgsmål: Hvad repræsenterer integralet af sandsynlighedsdensitetsfunktionen?

Svar: Integralet af sandsynlighedsdensitetsfunktionen repræsenterer sandsynligheden for, at en given tilfældig variabel med den givne tæthed er indeholdt i et givet interval.

Spørgsmål: Er sandsynlighedsdensitetsfunktionen altid ikke-negativ i hele sit område?

Svar: Ja, pr. definition er sandsynlighedsdensitetsfunktionen ikke-negativ i hele sit område.

Spørgsmål: Kan integrering over et interval give summen 1?

Svar: Ja, integrering over et interval summerer til 1.

Sp: Hvilken type fordeling karakteriserer en sandsynlighedsdensitetsfunktion?

Svar: En sandsynlighedsdensitetsfunktion karakteriserer enhver kontinuert sandsynlighedsfordeling.