Snells lov: Definition og formel for lysets brydning

Snells lov: klar definition og formel for lysets brydning. Forstå sammenhængen mellem indfaldsvinkel, brydningsvinkel og brydningsindeks med forklaring og eksempler.

Forfatter: Leandro Alegsa

15-12-2025 13:37

Snells brydningslov beskriver, hvordan lys (eller andre bølger) ændrer retning, når det passerer fra ét gennemskueligt medium til et andet. Loven er en grundlæggende videnskabelig lov inden for optik og gælder også for andre bølgers brydning. Når lys går fra ét materiale til et andet (fx fra luft til glas), fastlægger Snells lov et entydigt forhold mellem indfaldsvinklen og brydningsvinklen.

Formel

Snells lov kan skrives som

sin θ 1 sin θ 2 = v 1 v 2 = n 2 n 1 {\displaystyle {\frac {\sin \theta _{1}}}{\sin \theta _{2}}}}={\frac {v_{1}}}{v_{2}}}}={\frac {n_{2}}{n_{1}}}} ${\frac {\sin \theta _{1}}{\sin \theta _{2}}}={\frac {v_{1}}{v_{2}}}={\frac {n_{2}}{n_{1}}}$

I mere kompakt form bruges oftest den velkendte skrivemåde

n1 · sin θ1 = n2 · sin θ2

hvor θ måles fra grænsenormalen (vinkelret på overfladen). Ovenstående billede/ ligning (beholdt ovenfor) viser samme relation.

Tolkning og enheder

Med hver θ {\displaystyle \theta } $\theta$ forstås vinklen målt fra normalen til grænsefladen. v {\displaystyle v} $v$ er lysets fasehastighed i det pågældende medium (SI-enhed: meter pr. sekund, m/s). n {\displaystyle n} betegner mediets brydningsindeks.

Brydningsindekset i et vakuum er defineret som 1, og lysets hastighed i vakuum er c {\displaystyle c} $c$ . For et materiale relateres brydningsindekset til vakuumhastigheden ved

v = c/n ${\frac {c}{n}}$ .

Eksempel på typiske brydningsindekser: luft ≈ 1,0003 (ofte approximeret som 1), almindeligt glas ≈ 1,5, diamant ≈ 2,42. Konstanten c er cirka 3·10^8 m/s.

Bevis og fysisk forklaring

Snells lov kan afledes fra flere synsvinkler:

Fermats princip: Lyd eller lys vælger den sti, der minimerer rejsetiden. Ved at formulere total rejsetid som funktion af brudpunktet på grænsefladen og sætte den afledte lig nul fås n1 sin θ1 = n2 sin θ2. Dette var den oprindelige varianterede metode til bevis.
Huygens' princip: Ved at betragte hver bølgefront som et sæt af punktkilder, som danner ny bølgefront i næste medium, kan man geometrisk udlede relationen mellem vinklerne.
Bølgeégenskaber: Ved kontinuitet af fase parallel med grænsefladen må bølgevektorerne opfylde en bevarelse af den parallelle komponent, hvilket fører til samme matematisk udtryk.

Særlige tilfælde og konsekvenser

Normal indfald: Hvis θ1 = 0 (lys rammer vinkelret på overfladen), går lyset videre uden afbøjning (θ2 = 0).
Total intern refleksion: Når lys går fra et tætere medium (højere n) til et tyndere (lavere n), findes en kritisk vinkel θc, hvor sin θc = n2 / n1 for n1 > n2. For indfaldsvinkler større end θc sker total intern refleksion, og ingen refrakteret (overført) bølge findes. Fx glas (n≈1,5) → luft (n≈1,0) giver θc ≈ arcsin(1/1,5) ≈ 41,8°.
Grazing incidence: For vinkler tæt på 90° (meget skråt indfald) nærmer den refrakterede vinkel sig 90° efter Snell’s lov.
Dispergerende materialer: Brydningsindekset afhænger almindeligvis af bølgelængden (n = n(λ)). Det forklarer f.eks. opløsning af hvidt lys i et prisme, hvor forskellige bølgelængder bøjes forskelligt (kromatisk dispersion).
Absorberende medier: For medier med absorption er brydningsindekset komplekst (n = n' + iκ). Snells lov kan da benyttes i kompleks form, men fortolkning af vinkler og amplitude ændres (der optræder dæmpning i det absorberende medium).

Eksempel

Tag lys fra luft (n1 ≈ 1,00) ind i glas (n2 ≈ 1,50) med indfaldsvinkel θ1 = 30°.

Efter Snell: sin θ2 = (n1 / n2) · sin θ1 = (1,00 / 1,50) · sin 30° = (0,6667) · 0,5 = 0,3333 → θ2 ≈ arcsin(0,3333) ≈ 19,5°.

Anvendelser

Design af linser og optiske instrumenter (kameraer, mikroskoper, teleskoper).
Prismetekknik og spektralanalyse (dispersionsudnyttelse).
Optiske fibre og total intern refleksion til datatransmission.
Øjenlægevidenskab (kontaktlinser, glasstyrke) og mange industrielle optiske målinger.

Vigtige bemærkninger

Vinkler skal måles i forhold til normalen (ikke i forhold til overfladen).
Snells lov gælder i sin klassiske form for homogene, isotrope og ikke-dispersive medier; hvis medierne er anisotrope eller ikke-lineære, kræves mere avanceret behandling.
For eksakt beregning af hastigheder og bølgeegenskaber i materialer med frekvensafhængigt n, må man tage hensyn til materialets dispersionrelation.

Snells lov er altså både enkel og kraftfuld: den forbinder geometrien af lysstråler med mediers elektromagnetiske egenskaber (gennem brydningsindekset) og er fundamentet for størstedelen af klassisk geometrisk optik.

Snells lov kan bevises ved hjælp af Fermats princip. Fermats princip siger, at lyset bevæger sig ad den vej, der tager mindst tid.

En lysstråle rammer et glasprisme og brydes

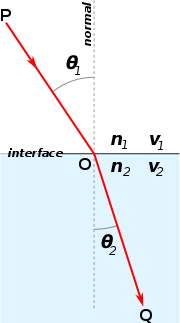
Lysets brydning ved grænsefladen mellem to medier med forskellige brydningsindeks, med n2 > n1

Historie

Ideen har en lang historie. Problemet har været genstand for opmærksomhed hos Hero af Alexandria, Ptolemæus, Ibn Sahl og Huygens. Ibn Sahl opdagede faktisk loven om brydning. I Traité de la Lumiere, 1678, viste Huygens, hvordan Snells lov om sinus kunne forklares ved eller afledes af lysets bølgenatur.

Spørgsmål og svar

Sp: Hvad er Snells lov om brydning?

A: Snells brydningslov er den videnskabelige lov om brydning af lys eller andre bølger. I optik siger den, at når lys passerer gennem forskellige materialer, ændres forholdet mellem sinus af indfalds- og brydningsvinklen ikke.

Spørgsmål: Hvordan kan Snells lov bevises?

Svar: Snells lov kan bevises ved hjælp af Fermats princip, som siger, at lyset bevæger sig ad den vej, der tager mindst mulig tid.

Spørgsmål: Hvad er Fermats princip?

A: Fermats princip siger, at lyset bevæger sig langs en vej, der tager mindst mulig tid.

Spørgsmål: Hvad er n og v i Snells lov?

Svar: n er et medies brydningsindeks, og v er lysets hastighed i det pågældende medium (målt i meter pr. sekund).

Sp: Hvad repræsenterer c i Snells lov?

Svar: c repræsenterer lysets hastighed i et vakuum, som har et brydningsindeks på 1.

Spørgsmål: Hvordan beregner man hastigheden, når en bølge passerer gennem et materiale med brydningsindeks n?

Svar: Hastigheden bliver c/n, når en bølge passerer gennem et materiale med et brydningsindeks n.

Søge