AlegsaOnline.com

Differentialregning: definition, historie og grundlæggende begreber

Lær differentialregning: klare definitioner, historisk baggrund og grundlæggende begreber for begyndere og viderekomne — fra Newton til Leibniz.

Forfatter: Leandro Alegsa

25-10-2025

Differentialregning, en gren af regnearket, er studiet af at bestemme, hvordan en variabel ændrer sig i forhold til en anden ved hjælp af funktioner. Kort sagt handler differentialregning om ændringshastigheder og om at beskrive, hvordan en funktion ændrer sig fra ét punkt til et andet uden at opdele kurven i uendeligt mange stykker. Det står i tæt forbindelse med integralregning, men fokuserer på øjeblikkelige ændringer i stedet for summering af små bidrag. Den moderne teori blev udviklet i 1670'erne og 1680'erne af Sir Isaac Newton og Gottfried Leibniz, som indførte de grundlæggende idéer og notationer.

Grundlæggende idé — differentialkvotienten

Differentialkvotienten (ofte kaldet derivatet) for en funktion f i punktet x beskriver den øjeblikkelige ændringshastighed af f ved x. Den formelle definition er givet ved grænseværdien

lim_h→0 (f(x+h) − f(x)) / h,

hvis denne grænseværdi eksisterer. Denne værdi skriver man typisk som f'(x), dy/dx eller Df(x).

Geometrisk og fysisk fortolkning

Geometrisk: f'(x) er hældningen af tangenten til grafen for f i punktet (x, f(x)).
Fysisk: Hvis f(t) beskriver en genstands position som funktion af tiden t, så er f'(t) genstandens hastighed på tidspunktet t.

Notationer

Der findes flere måder at skrive et derivat på, fx f'(x), df/dx eller Df(x). Newton brugte ofte prik-notationen (ḟ) til tidsderivater, mens Leibniz indførte dy/dx, som understreger "ændring i y divideret med ændring i x". Begge notationer er almindelige og nyttige i forskellige sammenhænge.

Vigtige egenskaber

Hvis en funktion er differentiabel i et punkt, er den også kontinuerlig i det punkt. Omvendt er kontinuitet ikke nok til differentiabilitet (fx har |x| et hjørne i 0 og er ikke differentiabel dér).
Man kan tage højere ordens derivater som f''(x), f'''(x) osv.; disse beskriver henholdsvis acceleration, ændring i acceleration osv. i fysiske anvendelser.

Regneregler (kort oversigt)

Konstant: (c)' = 0.
Potensregel: (x^n)' = n x^{n-1} for n ∈ ℝ (typisk n heltal i begyndelsen).
Sum og differens: (f+g)' = f' + g', (f−g)' = f' − g'.
Produktregel: (fg)' = f'g + fg'.
Kvotientregel: (f/g)' = (f'g − fg')/g^2, for g ≠ 0.
Kædereglen: Hvis y = f(u) og u = g(x), så dy/dx = (dy/du)·(du/dx). Denne regel er central ved sammensatte funktioner.

Nogle simple eksempler

f(x) = x^3 ⇒ f'(x) = 3x^2.
f(x) = sin x ⇒ f'(x) = cos x.
f(x) = e^x ⇒ f'(x) = e^x.
f(x) = a (konstant) ⇒ f'(x) = 0.

Hyppige anvendelser

Differentialregning bruges bredt i naturvidenskab, teknik, økonomi og statistik. Eksempler:

Bestemmelse af hastighed og acceleration i fysik.
Optimering: finde maksimum og minimum ved at sætte f'(x) = 0 og undersøge andenafledte.
Analyser af vækstrater i biologi og økonomi.
Linearisering og approksimation: brug af differentialer til at approksimere funktioner tæt på et punkt.

Historisk note

Udviklingen af differentialregning i slutningen af 1600-tallet revolutionerede matematik og naturvidenskab. Sir Isaac Newton og Gottfried Leibniz nåede uafhængigt frem til metoderne; Newton lagde vægt på anvendelser i mekanik og fluxioner, mens Leibniz introducerede den notation (dy/dx), som i høj grad lettede den videre udbygning og udbredelse af teorien. Der opstod historisk en strid om prioritet, men begge bidrag ventes i dag som grundlæggende for faget.

Afsluttende bemærkninger

Differentialregning giver et præcist sprog til at beskrive ændring. Når man lærer værktøjerne (definitionen via grænse, regneregler og fortolkninger), åbner det op for meget af moderne matematik og dens anvendelser. For videre læsning anbefales at arbejde med konkrete opgaver, grafiske fortolkninger og at studere sammenhængen mellem differential- og integralregning.

Baggrund

I modsætning til et tal som f.eks. 5 eller 200 kan en variabel ændre sin værdi. F.eks. er afstand og tid variabler. Ved et olympisk løb stiger afstanden fra startlinjen, efterhånden som personen løber. I mellemtiden måler et stopur eller et ur tiden, mens den stiger. Vi kan måle løberens gennemsnitshastighed, hvis vi dividerer den tilbagelagte distance med den tid, det tog. Men det siger ikke noget om, hvilken hastighed personen løb med præcis 1,5 sekund inde i løbet. Hvis vi havde afstanden på 1 sekund og afstanden på 2 sekunder, ville vi stadig kun have et gennemsnit, selv om det sandsynligvis ville være mere korrekt end gennemsnittet for hele løbet.

Indtil matematikken blev opfundet, var den eneste måde at regne dette ud på at skære tiden op i mindre og mindre stykker, så gennemsnitshastigheden over den mindre tid ville komme tættere og tættere på den faktiske hastighed på præcis 1,5 sekunder. Dette var en meget lang og besværlig proces, og den skulle udføres hver gang folk ville regne noget ud. Det er helt sikkert meget vanskeligere for en bilist at regne en bils hastighed ud ved kun at bruge dens kilometertæller (afstandsmåler) og ur - uden et speedometer.

Et meget lignende problem er at finde hældningen (hvor stejl den er) i et hvilket som helst punkt på en kurve. Hældningen af en ret linje er let at regne ud - den er simpelthen hvor meget den går opad (y eller lodret) divideret med hvor meget den går på tværs (x eller vandret). Hvis en linje er parallel med x-aksen, er dens hældning nul. Hvis en ret linje går gennem (x,y) = (2,10) og (4,18), går linjen 8 opad og 2 over, så dens hældning er 8 divideret med 2, hvilket er 4.

På en "kurve" er hældningen dog variabel (har forskellige værdier i forskellige punkter), fordi linjen bøjer sig. Men hvis kurven skulle skæres i meget, meget små stykker, ville kurven i punktet næsten ligne en meget kort ret linje. Så for at beregne dens hældning kan man tegne en ret linje gennem punktet med samme hældning som kurven i det pågældende punkt. Hvis det gøres helt rigtigt, vil den rette linje have samme hældning som kurven, og den kaldes en tangent. Men der er ingen måde at vide (uden beregning), om tangenten er nøjagtig rigtig, og vores øjne er ikke præcise nok til at være sikre på, om den er nøjagtig eller blot meget tæt på.

Newton og Leibniz fandt en måde at beregne hældningen (eller hastigheden i eksemplet med afstanden) nøjagtigt ved hjælp af enkle og logiske regler. De opdelte kurven i et uendeligt antal meget små stykker. Derefter valgte de punkter på hver side af det punkt, de var interesseret i, og udregnede tangenter ved hvert punkt. Efterhånden som punkterne kom tættere på hinanden i retning af det punkt, de var interesseret i, nærmede hældningen sig en bestemt værdi, efterhånden som tangenterne nærmede sig kurvens reelle hældning. De sagde, at denne særlige værdi, som den nærmede sig, var den faktiske hældning.

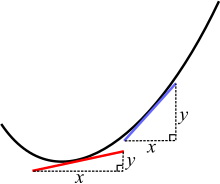
På en kurve har to forskellige punkter forskellige hældninger. Den røde og den blå linje er tangenter til kurven.

Sådan fungerer det

Lad os sige, at vi har en funktion y = f(x). f er en forkortelse for funktion, så denne ligning betyder "y er en funktion af x". Det fortæller os, at hvor højt y er på den lodrette akse, afhænger af, hvad x (den vandrette akse) er på det pågældende tidspunkt. Med ligningen y = x² ved vi f.eks., at hvis x er 1, vil y være 1; hvis x er 3, vil y være 9; hvis x er 20, vil y være 400.

Vælg et punkt A på kurven, og kald dets vandrette position x. Vælg derefter et andet punkt B på kurven, som ligger lidt længere på tværs end A, og kald dets vandrette position x + h. Det er ligegyldigt, hvor meget h er; det er et meget lille tal.

Så når vi går fra punkt A til punkt B, er den lodrette position gået fra f(x) til f(x + h), og den vandrette position er gået fra x til x + h. Husk nu, at hældningen er, hvor meget det går opad divideret med, hvor meget det går på tværs. Så hældningen vil være:

f ( x + h ) - f ( x ) h {\displaystyle {\frac {\frac {f(x+h)-f(x)}{h}}} ${\frac {f(x+h)-f(x)}{h}}$

Hvis du bringer B tættere og tættere på A - hvilket betyder, at h kommer tættere og tættere på 0 - så kommer vi tættere på at vide, hvad hældningen er i punktet A.

lim h → 0 f ( x + h ) - f ( x ) h {\displaystyle \lim _{h\rightarrow 0}{\frac {f(x+h)-f(x)}{h}}} $\lim _{h\rightarrow 0}{\frac {f(x+h)-f(x)}{h}}$

Lad os nu gå tilbage til y = x². Hældningen af dette kan bestemmes på følgende måde:

= lim h → 0 f ( x + h ) - f ( x ) h = lim h → 0 ( x + h ) 2 - ( x ) 2 h {\displaystyle {\begin{aligned}&=\lim _{h\rightarrow 0}{\frac {f(x+h)-f(x)}{h}}\\&&=\lim _{h\rightarrow 0}{\frac {(x+h)^{2}-(x)^{2}}}{h}}\end{aligned}}}} ${\begin{aligned}&=\lim _{h\rightarrow 0}{\frac {f(x+h)-f(x)}{h}}\\&=\lim _{h\rightarrow 0}{\frac {(x+h)^{2}-(x)^{2}}{h}}\end{aligned}}$

Ved at anvende binomialsatsen, som bl.a. siger, at ( x + y ) 2 = x 2 + 2 x y + y 2 {\displaystyle (x+y)^{2}=x^{2}+2xy+y^{2}}} $(x+y)^{2}=x^{2}+2xy+y^{2}$ , kan vi reducere udtrykket til:

= lim h → 0 x 2 + 2 x h + h 2 - x 2 h = lim h → 0 2 x h + h 2 h = lim h → 0 2 x + h = 2 x {\displaystyle {\begin{aligned}&=\lim _{h\rightarrow 0}{\frac {x^{2}+2xh+h^{2}-x^{2}}}{h}}\&=\lim _{h\rightarrow 0}{\frac {2xh+h^{2}}}{h}}\&=\lim _{h\rightarrow 0}2x+h\\&={\frac {}{}}2x\end{aligned}}}} ${\begin{aligned}&=\lim _{h\rightarrow 0}{\frac {x^{2}+2xh+h^{2}-x^{2}}{h}}\\&=\lim _{h\rightarrow 0}{\frac {2xh+h^{2}}{h}}\\&=\lim _{h\rightarrow 0}2x+h\\&={\frac {}{}}2x\end{aligned}}$

Vi ved altså uden at skulle tegne nogen tangentlinjer, at i ethvert punkt på kurven f(x) = x² vil den afledte f'(x) (markeret med apostrof) være 2x i ethvert punkt. Denne proces med at regne en hældning ud ved hjælp af grænser kaldes differentiering eller at finde den afledte.

Leibniz nåede frem til det samme resultat, men kaldte h "dx", hvilket betyder "en lillebitte mængde af x". Han kaldte den resulterende ændring af f(x) for "dy", hvilket betyder "en lillebitte mængde y". Leibniz' notation anvendes af flere bøger, fordi den er let at forstå, når ligningerne bliver mere komplicerede. I Leibniz' notation:

d y d x = f ′ ( x ) {\displaystyle {\frac {dy}{dx}}}=f'(x)} ${\frac {dy}{dx}}=f'(x)$

Et billede, der viser, hvad x og x + h betyder på kurven.

Regler

Ved hjælp af ovenstående system har matematikere udarbejdet regler, som altid fungerer, uanset hvilken funktion man ser på. (Bemærk: her er u {\displaystyle u} $u$ og v {\displaystyle v} $v$ begge funktioner af x {\displaystyle x} )

Betingelse	Funktion	Derivat	Eksempel	Derivat
Et tal i sig selv	y = a {\displaystyle y=a} $y=a$	d y d d x = 0 {\displaystyle {\frac {dy}{dx}}=0}} ${\frac {dy}{dx}}=0$	y = 3 {\displaystyle y=3} $y=3$	0 {\displaystyle 0} $0$
En lige linje	y = m x + c {\displaystyle y=mx+c} $y=mx+c$	d y d x = m {\displaystyle {\frac {dy}{dx}}=m} ${\frac {dy}{dx}}=m$	y = 3 x + 5 {\displaystyle y=3x+5} $y=3x+5$	3 {\displaystyle 3} $3$
x til potens af et tal	x a {\displaystyle x^{a}} $x^{a}$	d y d x = a x a a - 1 {\displaystyle {\frac {dy}{dx}}}=ax^{a-1}}} ${\frac {dy}{dx}}=ax^{a-1}$	x 12 {\displaystyle x^{12}} $x^{12}$	12 x 11 {\displaystyle 12x^{11}} $12x^{11}$
Et tal multipliceret med en funktion	y = c ⋅ u {\displaystyle y=c\cdot u} $y=c\cdot u$	d y d d x = c d u d d x {\displaystyle {\frac {\frac {dy}{dx}}}=c{\frac {du}{dx}}}} ${\frac {dy}{dx}}=c{\frac {du}{dx}}$	y = 3 ( x 2 + x ) {\displaystyle y=3(x^{{2}+x)} $y=3(x^{2}+x)$	3 ( 2 x + 1 ) {\displaystyle 3(2x+1)} $3(2x+1)$
En funktion plus en anden funktion	y = u + v {\displaystyle y=u+v} $y=u+v$	d y d x = d u d x + d v d x {\displaystyle {\frac {dy}{dx}}}={\frac {du}{dx}}}+{\frac {dv}{dx}}}} ${\frac {dy}{dx}}={\frac {du}{dx}}+{\frac {dv}{dx}}$	y = 3 x 2 + x {\displaystyle y=3x^{2}+{\sqrt {x}}} $y=3x^{2}+{\sqrt {x}}$	6 x + 1 2 x {\displaystyle 6x+{\frac {1}{2{\sqrt {x}}}}} $6x+{\frac {1}{2{\sqrt {x}}}}$
En funktion minus en anden funktion	y = u - v {\displaystyle y=u-v} $y=u-v$	d y d x = d u d x - d v d x {\displaystyle {\frac {dy}{dx}}}={\frac {du}{dx}}}}-{\frac {dv}{dx}}}} ${\frac {dy}{dx}}={\frac {du}{dx}}-{\frac {dv}{dx}}$	y = 3 x 2 - x {\displaystyle y=3x^{2}-{\sqrt {x}}} $y=3x^{2}-{\sqrt {x}}$	6 x - 1 2 x {\displaystyle 6x-{\frac {1}{2{\sqrt {x}}}}} $6x-{\frac {1}{2{\sqrt {x}}}}$
Produktregel En funktion ganget med en anden funktion	y = u ⋅ v {\displaystyle y=u\cdot v} $y=u\cdot v$	d y d x = d u d x v + u d v d x {\displaystyle {\frac {dy}{dx}}}={\frac {du}{dx}}}v+u{\frac {dv}{dx}}}} ${\frac {dy}{dx}}={\frac {du}{dx}}v+u{\frac {dv}{dx}}$	y = ( x 2 + x + 2 ) ( 3 x - 1 ) {\displaystyle y=(x^{2}+x+2)(3x-1)} $y=(x^{2}+x+2)(3x-1)$	( 3 x - 1 ) ( 2 x + 1 ) + 3 ( x 2 + x + x + 2 ) {\displaystyle (3x-1)(2x+1)+3(x^{2}+x+2)} $(3x-1)(2x+1)+3(x^{2}+x+2)$
Kvotientregel En funktion divideret med en anden funktion	y = u v {\displaystyle y={\frac {u}{v}}}} $y={\frac {u}{v}}$	d y d x = d u d x v - u d v d x v 2 {\displaystyle {\frac {\frac {dy}{dx}}}={\frac {{\frac {{\frac {du}{dx}}}v-u{\frac {dv}{dv}{dx}}}{v^{2}}}} ${\frac {dy}{dx}}={\frac {{\frac {du}{dx}}v-u{\frac {dv}{dx}}}{v^{2}}}$	y = x 2 + 2 x - 1 {\displaystyle y={{\frac {x^{2}+2}{x-1}}}} $y={\frac {x^{2}+2}{x-1}}$	2 x ( x - 1 ) - ( x 2 + 2 ) ( x - 1 ) 2 {\displaystyle {\frac {\frac {2x(x-1)-(x^{2}+2)}{(x-1)^{2}}}} ${\frac {2x(x-1)-(x^{2}+2)}{(x-1)^{2}}}$
Kædningsregel Anvendes til sammensatte funktioner	y = u ∘ v {\displaystyle y=u\circ v} $y=u\circ v$	d y d x = d y d u ⋅ d u d x {\displaystyle {\frac {dy}{dx}}}={\frac {dy}{du}}}\cdot {\frac {du}{dx}}}} ${\frac {dy}{dx}}={\frac {dy}{du}}\cdot {\frac {du}{dx}}$	y = 2 x - 1 {\displaystyle y={{\sqrt {2x-1}}}} $y={\sqrt {2x-1}}$	2 2 2 2 2 x - 1 = 1 2 x - 1 {\displaystyle {\frac {2}{2{\sqrt {2x-1}}}}={\frac {1}{\sqrt {2x-1}}}} ${\frac {2}{2{\sqrt {2x-1}}}}={\frac {1}{\sqrt {2x-1}}}$
En eksponentiel funktion	y = e x {\displaystyle {\frac {}{}}}y=e^{x}} ${\frac {}{}}y=e^{x}$	d y d x = e x {\displaystyle {\frac {dy}{dx}}}=e^{x}} ${\frac {dy}{dx}}=e^{x}$	y = e x {\displaystyle {\frac {}{}}}y=e^{x}} ${\frac {}{}}y=e^{x}$	e x {\displaystyle {\frac {}{}{}}e^{x}} ${\frac {}{}}e^{x}$

Relaterede sider

Derivat (matematik)
Differentialoperator
Ordinær differentialligning
Matematisk analyse

Spørgsmål og svar

Q: Hvad er differentialregning?

A: Differentialregning er en gren af regnearket, der undersøger ændringshastigheden for en variabel i forhold til en anden variabel ved hjælp af funktioner.

Q: Hvordan virker det?

A: Differentialregning giver os mulighed for at finde ud af, hvordan en form ændrer sig fra et punkt til det næste uden at skulle dele formen op i uendeligt mange stykker.

Spørgsmål: Hvem har udviklet differentialregning?

Svar: Differentialregning blev udviklet i 1670'erne og 1680'erne af Sir Isaac Newton og Gottfried Leibniz.

Spørgsmål: Hvad er integralregning?

Svar: Integralregning er det modsatte af differentialregning. Den bruges til at finde arealer under kurver og rumfang af faste legemer med krumme overflader.

Spørgsmål: Hvornår blev differentialregning udviklet?

Svar: Differentialregning blev udviklet i 1670'erne og 1680'erne af Sir Isaac Newton og Gottfried Leibniz.

Spørgsmål: Hvad er nogle anvendelser af differentialregning?

Svar: Nogle af differentialkalkuliens anvendelser omfatter beregning af hastighed, acceleration, maksimum- eller minimumsværdier, optimeringsproblemer, hældningsfelter osv.

Spørgsmål: Hvorfor bruger vi differentialregning i stedet for at opdele figurer i et uendeligt antal stykker?

A: Vi bruger differentialregning i stedet for, fordi det giver os mulighed for at finde ud af, hvordan en form ændrer sig fra et punkt til det næste uden at skulle dele formen op i et uendeligt antal stykker.