AlegsaOnline.com

Eksponentiel funktion (e^x): Definition, egenskaber og anvendelser

Lær eksponentiel funktion (e^x): klar definition, nøgleegenskaber, intuitiv forklaring og praktiske anvendelser inden for matematik, fysik og økonomi.

Forfatter: Leandro Alegsa

11-02-2026

I matematik er den eksponentielle funktion en funktion, der vokser hurtigere og hurtigere. Mere præcist er det funktionen $\exp(x)=e^{x}$ , hvor e er Eulers konstant, et irrationalt tal, der er ca. 2,71828.

Definition og notation

Eksponentiel funktion betegnes ofte som e^x eller exp(x). Dens definitionsmængde er alle reelle tal (x ∈ R), og værdimængden er de positive reelle tal (e^x > 0 for alle x).

Vigtige egenskaber

Derivata: d/dx e^x = e^x. Det betyder, at den afledte funktion er identisk med funktionen selv.
Integral: ∫ e^x dx = e^x + C. For sammensatte argumenter: ∫ e^{ax} dx = (1/a)e^{ax} + C.
Regneregler: e^{x+y} = e^x e^y, e^{0} = 1, e^{-x} = 1/e^x, (e^x)^k = e^{kx} og e^{x-y} = e^x / e^y.
Monotoni og kontinuitet: e^x er strengt voksende, kontinuerlig og differentiabel over hele R.
Grænseværdier: lim_{x→∞} e^x = ∞ og lim_{x→-∞} e^x = 0 (vandret asymptote y = 0 modtages fra venstre).
Inverterbar: Den inverse funktion er den naturlige logaritme ln(x), således at ln(e^x) = x for alle x og e^{ln y} = y for y > 0.

Alternative definitioner af e

Som grænse: e = lim_{n→∞} (1 + 1/n)^n.
Som sum af en række: e = ∑_{n=0}^{∞} 1/n! (hvor n! er n-fakultet).
Som den positive talværdi der gør, at funktionen a^x har afledt 1 i x = 0; for a = e fås d/dx e^x|_{x=0} = 1.

Taylor- og potensrække

Eksponentialfunktionen har en globalt konvergent potensrække omkring 0:

e^x = ∑_{n=0}^{∞} x^n / n! for alle x ∈ R (radius for konvergens er ∞).

Sammensatte funktioner og kædereglen

For en differentiabel funktion f(x) gælder:

d/dx e^{f(x)} = f'(x) e^{f(x)}.

Kompleks udvidelse

Funktionen kan udvides til komplekse tal. En central identitet er Eulers formel:

e^{ix} = cos x + i sin x for x ∈ R, hvor i er den imaginære enhed. Denne forbindelse binder eksponentialfunktionen til trigonometriske funktioner.

Typiske anvendelser

Kontinuerlig rentetilvækst: A(t) = P e^{rt}, hvor P er startkapital, r rente pr. tidsenhed og t tiden.
Population og vækstmodeller: Hvis vækstraten er proportional med størrelsen, får man N(t) = N_0 e^{kt}.
Radioaktivt henfald: Mængden følger ofte N(t) = N_0 e^{-λt}, hvor λ er henfaldskonstanten.
Sandsynlighedsfordelinger: Normalfordelingen indeholder e i eksponenten: f(x) = (1/(√(2π)σ)) e^{- (x-μ)^2 / (2σ^2)}.
Differentialligninger: Løsninger til y' = ky er y = Ce^{kt}. Eksponentialfunktionen optræder derfor i mange fysiske modeller (varmeledning, vækst, dæmpning osv.).
Signalbehandling og Fouriertransform: e^{ix} er fundamentalt i komplekse eksponenter og harmonisk analyse.

Eksempler

Afledt af e^{3x} er 3e^{3x}.
∫ e^{2x} dx = (1/2) e^{2x} + C.
Omskriv base a: a^x = e^{x ln a} (bruges ved beregninger med anden eksponentiel base).

Grafisk opførsel

Grafen skærer y-aksen i y = 1 (ved x = 0). For negative x nærmer grafen sig y = 0 uden nogensinde at ramme den. For positive x stiger grafen hurtigt og bliver meget stor. Dette gør e^x til en naturlig model for processer med accelererende vækst.

Bemærkninger og gode huskeregler

Notationen e^x og exp(x) bruges om hinanden; exp(x) er ofte praktisk i programmering og videnskabelige sammenhænge.
Husk regnereglerne for eksponenter, især e^{x+y} = e^x e^y, når du forenkler udtryk.
På mange områder i matematik og naturvidenskab er e^x den mest naturlige vækstfunktion, fordi den bevarer sin form under differentiation og integration.

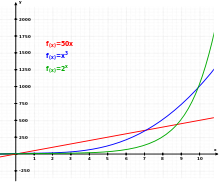
Tre forskellige funktioner: Lineær (rød), kubisk (blå) og eksponentiel (grøn).

Egenskaber

Da eksponentielle funktioner anvender eksponering, følger de de samme regler for eksponenter. Således,

$e^{x+y}=\exp(x+y)=\exp(x)\exp(y)=e^{x}e^{y}$ .

Dette følger reglen om, at x a ⋅ $x^{a}\cdot x^{b}=x^{a+b}$ .

Den naturlige logaritme er den omvendte operation af en eksponentialfunktion, hvor:

$\ln(x)=\log _{e}(x)={\frac {\log(x)}{\log(e)}}$

Den eksponentielle funktion opfylder en interessant og vigtig egenskab i differentialregning:

${\frac {\mathrm {d} }{\mathrm {d} x}}e^{x}=e^{x}$

Det betyder, at hældningen af den eksponentielle funktion er selve den eksponentielle funktion, og som følge heraf har hældningen 1 ved x = 0 {\displaystyle x=0} $x=0$ . Disse egenskaber er grunden til, at det er en vigtig funktion i matematikken.

Anvendelser

Den generelle eksponentialfunktion, hvor basen ikke nødvendigvis er e {\displaystyle e} $e$ , er blandt de mest nyttige matematiske funktioner. Den bruges til at repræsentere eksponentiel vækst, som anvendes inden for stort set alle videnskabelige discipliner og er også fremtrædende inden for finansverdenen. En anden anvendelse af den eksponentielle funktion er eksponentiel henfald, som forekommer ved radioaktivt henfald og absorption af lys.

Et eksempel på en eksponentiel funktion i det virkelige liv er renter i en bank. Hvis en person indbetaler 100 £ på en konto, som får 3 % rente om måneden, vil saldoen hver måned (hvis pengene ikke røres) være som følger:

Måned	Balance	Måned	Balance
Januar	£100.00	Juli	£119.41
Februar	£103.00	August	£122.99
Marts	£106.09	September	£126.68
April	£109.27	Oktober	£130.48
maj	£112.55	November	£134.39
Juni	£115.93	December	£138.42

Her kan du se, hvordan de ekstra penge fra renterne stiger hver måned, idet jo større den oprindelige saldo er, jo flere renter får personen.

To matematiske eksempler på eksponentielle funktioner (med base a) er vist nedenfor.

a=2

x {\displaystyle x}	Resultat
-2	0.25
-1	0.5
0	1
1	2
2	4
3	8
4	16

a=3

x {\displaystyle x}	Resultat
-2	¹/ ₉
-1	¹/ ₃
0	1
1	3
2	9
3	27
4	81

Forholdet til den matematiske konstant e

Selv om basen ( a {\displaystyle a} ) kan være et hvilket som helst tal større end nul, f.eks. 10 eller 1/2, er det ofte et særligt tal kaldet e. Tallet e kan ikke skrives præcist, men det er næsten lig med 2,71828.

Tallet e er vigtigt for enhver eksponentialfunktion. En bank betaler f.eks. en rente på 0,01 procent hver dag. En person tager sine rentepenge og lægger dem i en kasse. Efter 10 000 dage (ca. 30 år) har han 2 gange så mange penge, som han startede med. En anden person tager sine rentepenge og sætter dem tilbage i banken. Fordi banken nu betaler ham renter af sine renter, er pengebeløbet en eksponentiel funktion.

Faktisk har han efter 10.000 dage ikke 2 gange så mange penge, som han startede med, men han har 2,718145 gange så mange penge, som han startede med. Dette tal ligger meget tæt på tallet e. Hvis banken betaler renter oftere, så det beløb, der betales hver gang, er mindre, vil tallet ligge tættere på tallet e.

Man kan også se på billedet for at se, hvorfor tallet e er vigtigt for eksponentielle funktioner. Billedet har tre forskellige kurver. Kurven med de sorte punkter er en eksponentialfunktion med en base lidt mindre end e. Kurven med de korte sorte streger er en eksponentialfunktion med en base lidt større end e. Den blå kurve er en eksponentialfunktion med en base, der er nøjagtig lig med e. Den røde linje er en tangent til den blå kurve. Den berører den blå kurve i et punkt uden at krydse den. En person kan se, at den røde kurve krydser x-aksen, den linje, der går fra venstre mod højre ved -1. Dette gælder kun for den blå kurve. Dette er grunden til, at den eksponentielle funktion med basen e er speciel.

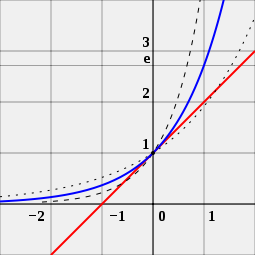
e er det eneste tal a, som gør, at værdien af den afledte af den eksponentielle funktion f (x) = ax (blå kurve) i punktet x = 0 er præcis 1. Til sammenligning er vist funktionerne 2x (stiplet kurve) og 4x (stiplet kurve); de tangerer ikke linjen med hældning 1 (rød).

Relaterede sider

Logaritme

Spørgsmål og svar

Spørgsmål: Hvad er den eksponentielle funktion?

A: Den eksponentielle funktion er en matematisk funktion, der vokser hurtigere og hurtigere.

Q: Hvordan udtrykkes den eksponentielle funktion matematisk?

A: Den eksponentielle funktion udtrykkes matematisk som exp(x) = e^x, hvor e er Eulers konstant.

Spørgsmål: Hvad repræsenterer Eulers konstant?

A: Eulers konstant er et irrationelt tal, som er ca. 2,71828.

Spørgsmål: Er den eksponentielle funktion altid stigende?

Svar: Ja, den eksponentielle funktion stiger altid i værdi, når x stiger.

Spørgsmål: Er der nogen grænse for, hvor hurtigt den eksponentielle funktion kan vokse?

Svar: Nej, der er ingen grænse for, hvor hurtigt den eksponentielle funktion kan vokse, da den fortsætter med at stige med større værdier af x.

Spørgsmål: Hvordan kan vi beregne Eulers konstant?

A: Vi kan beregne Eulers konstant ved hjælp af numeriske metoder som Taylor-serier eller fortsatte brøker.

Spørgsmål: Hvilke andre anvendelsesmuligheder er der for den eksponentielle funktion ud over matematik?

A: Eksponentialfunktionen har mange anvendelser uden for matematikken, herunder fysik, kemi, biologi, økonomi og ingeniørvidenskab.