Overfladeintegral — definition, beregning og anvendelser i matematik og fysik
Guide til overfladeintegral: definition, beregning og praktiske anvendelser i matematik og fysik — forstå skalar- og vektorfelter samt elektromagnetisme.
I matematikken er et overfladeintegral et bestemt integral over en overflade (som kan være en kurve i rummet). Ligesom et linieintegral behandler én dimension eller én variabel, kan et overfladeintegral betragtes som et dobbeltintegral i to dimensioner. På en overflade kan man integrere over dens skalarfelter (dvs. funktioner, der returnerer tal som værdier) og vektorfelter (dvs. funktioner, der returnerer vektorer som værdier).
Overfladeintegraler har anvendelser inden for fysik, især i den klassiske teori om elektromagnetisme.
Hvad er et overfladeintegral?
Et overfladeintegral summerer en størrelse over en to-dimensionel flade i rummet. Man skelner hovedsageligt mellem to typer:
- Overfladeintegral af en skalarfunktion: ∬_S f dS, som måler den samlede “værdi” af f fordelt over overfladen S (fx masse af en tynd skal med varierende densitet).
- Overfladeintegral af et vektorfelt (flux): ∬_S F · n dS, som måler hvor meget af vektorfeltet F der passerer gennem overfladen S i retning af en valgt normal n (fx volumenstrøm gennem et område).
Beregningsmetoder
Den praktiske beregning bygger oftest på en parametrisering af overfladen. Hvis overfladen S parametrisers ved r(u,v) for (u,v) i et parameterområde D, gælder:
- Overfladeelement: dS = |r_u × r_v| du dv, hvor r_u og r_v er de partielle afledte af r efter u og v, og × er krydsproduktet.
- Skalarfelt: ∬_S f dS = ∬_D f(r(u,v)) |r_u × r_v| du dv.
- Vektorfelt (flux): ∬_S F · n dS = ∬_D F(r(u,v)) · (r_u × r_v) du dv. Her bruges r_u × r_v som en orienteret (ikke-normaliseret) normalvektor; hvis man ønsker enhedsnormalen n, deles med |r_u × r_v| og multipliceres igen med dS.
Eksempler
1) Overfladeareal af en kugle med radius R:
Parametriser med sfæriske koordinater: r(θ,φ) = (R sin φ cos θ, R sin φ sin θ, R cos φ), 0 ≤ θ < 2π, 0 ≤ φ ≤ π. Så |r_θ × r_φ| = R^2 sin φ, og
Area(S) = ∬_S dS = ∫_{0}^{2π} ∫_{0}^{π} R^2 sin φ dφ dθ = 4π R^2.
2) Flux gennem en kugle for F(x,y,z) = (x,y,z):
Enten direkte: på kuglen |r| = R er F·n = r·n = R, så ∬_S F·n dS = R ∬_S dS = R · 4π R^2 = 4π R^3.
Eller via Gauss' divergensteorem: div F = 3, og fluxen = ∭_V div F dV = 3 · Vol(B_R) = 3 · (4/3)π R^3 = 4π R^3.
Overflader givet som grafer eller implicitte funktioner
- Hvis overfladen er en graf z = f(x,y) over et område A i xy-planet, er dS = sqrt(1 + f_x^2 + f_y^2) dx dy. En enhedsnormal kan skrives som ±(-f_x, -f_y, 1) / sqrt(1 + f_x^2 + f_y^2).
- Hvis overfladen er givet implicit ved G(x,y,z) = 0, peger normalvektoren lokalt i retning af ∇G = (G_x, G_y, G_z). Under passende betingelser kan man lokalt løse for en variabel og anvende graf-formlen.
Relationer til øvrige teoremer
- Gauss' (divergens) teorem: For et lukket område V med randoverflade S: ∬_S F · n dS = ∭_V div F dV. Denne forbindelse gør beregning af flux lettere, når man kender divergensen.
- Stokes' teorem: Relaterer et overfladeintegral af curl F over en åben overflade S til et linieintegral langs randkurven ∂S: ∬_S (curl F) · n dS = ∮_{∂S} F · dr.
Anvendelser i fysik og teknik
- Elektromagnetisme: Gauss' lov forbinder elektrisk flux gennem en lukket overflade med den indespærrede ladning — grundlæggende i elektrostatik.
- Fluidmekanik: Flux ∬_S v · n dS giver mængden af væske, der passerer en overflade pr. tidsenhed.
- Varmeledning og stoftransport: Beregning af transport gennem membraner eller skaller.
- Computergrafik og geometri: Overfladeareal, belysningsberegninger og mesh-behandling anvender diskrete overfladeintegraler.
Numeriske metoder
I praksis beregnes overfladeintegraler ofte numerisk:
- Triangulering / meshing: Overfladen opdeles i små trekanter; integralet approksimeres som sum over elementerne (finite element / finite volume).
- Monte Carlo: Stokastisk sampling af punkter på overfladen bruges til estimater, især i høje dimensioner eller for komplekse flader.
- Parametrisk kvadratur: Når en god parametriseringen findes, kan man anvende standard kvadraturregler i parameterrummet.
Praktiske tips ved udregning
- Vælg en parametrisering der udnytter symmetri (sfæriske eller cylindriske koordinater ofte for kugler eller cylindre).
- Vær opmærksom på orienteringen af normalvektoren — for lukkede overflader vælges normalt udadrettet normal.
- Kontroller randbetingelser og singulariteter (fx punkter hvor r_u × r_v = 0 kræver særlig opmærksomhed).
- Brug teoremer (Gauss, Stokes) når det forenkler opgaven.
Samlet set er overfladeintegraler et centralt værktøj i både teoretisk og anvendt matematik, især når man skal beskrive og kvantificere, hvordan skalarer og vektorer fordeler sig over eller passerer gennem flader i rummet.
Definitionen af overfladeintegral er baseret på en opdeling af overfladen i små overfladeelementer.
En illustration af et enkelt overfladeelement. Disse elementer gøres uendeligt små ved begrænsningsprocessen, så de tilnærmer sig overfladen.
Overfladeintegraler af skalarfelter
Betragt en overflade S, hvorpå et skalarfelt f er defineret. Hvis man betragter S som værende lavet af et eller andet materiale, og for hvert x i S er tallet f(x) tætheden af materialet ved x, så er overfladeintegralet af f over S masse pr. tykkelsesenhed af S. (Dette er kun sandt, hvis overfladen er en uendeligt tynd skal.) En metode til beregning af overfladeintegralet er at dele overfladen op i mange meget små stykker, antage at tætheden på hvert stykke er nogenlunde konstant, finde massen pr. tykkelsesenhed for hvert stykke ved at multiplicere tætheden af stykket med dets areal og derefter summere de resulterende tal for at finde den samlede masse pr. tykkelsesenhed af S.
For at finde en eksplicit formel for overfladeintegralet parameteriserer matematikere S ved at betragte S som et system af krumme koordinater, som f.eks. bredde- og længdegrader på en kugle. Lad en sådan parameterisering være x(s, t), hvor (s, t) varierer i et område T i planen. Så er overfladeintegralet givet ved
∫ S f d S = ∬ T f ( x ( s , t ) ) | ∂ x ∂ s × ∂ x ∂ t | d s d t {\displaystyle \int _{S}f\,dS=\iint _{T}f(\mathbf {x} (s,t))\left|{{\partial \mathbf {x} \over \partial s}\times {\partial \mathbf {x} \over \partial t}\right|ds\,dt} 
hvor udtrykket mellem søjlerne på højre side er størrelsen af krydsproduktet af de partielle afledte af x(s, t).
For at finde overfladearealet af en generel funktionel form, f.eks. z = f ( x , y ) {\displaystyle z=f\,(x,y)}
, har vi f.eks.
A = ∫ S d S = ∬ T ‖ ∂ r ∂ x × ∂ r ∂ y ‖ d x d y {\displaystyle A=\int _{S}\,dS=\iint _{T}\left\|{{\partial \mathbf {r} \over \partial x}\times {\partial \mathbf {r} \over \partial y}\right\|dx\,dy} 
hvor r = ( x , y , z ) = ( x , y , f ( x , y ) ) {\displaystyle \mathbf {r} =(x,y,z)=(x,y,f(x,y))}
. Så at ∂ r ∂ x = ( 1 , 0 , f x ( x , y ) ) {\displaystyle {\partial \mathbf {r} \over \partial x}=(1,0,f_{x}(x,y))} 
, og ∂ r ∂ y = ( 0 , 1 , f y ( x , y ) ) {\displaystyle {\partial \mathbf {r} \over \partial y}=(0,1,f_{y}(x,y))}
. Så,
A = ∬ T ‖ ( 1 , 0 , ∂ f ∂ x ) × ( 0 , 1 , ∂ f ∂ y ) ‖ d x d y = ∬ T ‖ T ‖ ( - ∂ f ∂ x , - ∂ f ∂ y , 1 ) ‖ d x d y = ∬ T ( ∂ f ∂ x ) 2 + ( ∂ f ∂ y ) 2 + 1 d x d y {\displaystyle {\begin{aligned}A&{}=\iint _{T}\left\|\left(1,0,{\partial f \over \partial x}\right)\times \left(0,1,{\partial f \over \partial y}\right)\right\|dx\,dy\\&{}=\iint _{T}\left\\\\left(-{\partial f \over \partial x},-{\partial f \over \partial y},1\right)\right\|dx\,dy\&{}=\iint _{T}{\sqrt {{\left({\partial f \over \partial x}\right)^{2}+\left({\partial f \over \partial y}\right)^{2}+1}}}\,\,dx\,dy\end{aligned}}}} 
som er den formel, der anvendes til beregning af overfladearealet af en generel funktionel form. Man kan genkende vektoren i den anden linje ovenfor som normalvektoren til overfladen.
Bemærk, at på grund af tilstedeværelsen af krydsproduktet fungerer ovenstående formler kun for overflader, der er indlejret i det tredimensionelle rum.
Overfladeintegraler af vektorfelter
Betragt et vektorfelt v på S, dvs. for hvert x i S er v(x) en vektor.
Overfladeintegralet kan defineres komponentvis i overensstemmelse med definitionen af overfladeintegralet af et skalarfelt; resultatet er en vektor. Dette gælder f.eks. for det elektriske felt i et fast punkt på grund af en elektrisk ladet overflade eller tyngdekraften i et fast punkt på grund af en materialebane. Den kan også beregne den magnetiske strøm gennem en overflade.
Alternativt kan matematikere integrere den normale komponent af vektorfeltet; resultatet er en skalar. Et eksempel er en væske, der strømmer gennem S, således at v(x) bestemmer væskens hastighed ved x. Strømmen er defineret som den mængde væske, der strømmer gennem S i en tidsenhed.
Denne illustration indebærer, at hvis vektorfeltet er tangent til S i hvert punkt, er strømmen nul, fordi væsken kun strømmer parallelt med S og hverken ind eller ud. Dette indebærer også, at hvis v ikke kun flyder langs S, dvs. hvis v har både en tangential- og en normal komponent, er det kun den normale komponent, der bidrager til strømmen. Baseret på dette ræsonnement skal vi for at finde strømmen tage prikproduktet af v med enhedsfladenormalen til S i hvert punkt, hvilket vil give os et skalarfelt, og integrere det opnåede felt som ovenfor. Dette giver formlen
∫ S v ⋅ d S = ∫ S ( v ⋅ n ) d S = ∬ T v ( x ( s , t ) ) ⋅ ( ∂ x ∂ s × ∂ x ∂ t ) d s d t . {\displaystyle \int _{S}{\mathbf {v} }\cdot \,d{\mathbf {S} }=\int _{S}({\mathbf {v} }\cdot {\mathbf {n} })\,dS=\iint _{T}{\mathbf {v} }(\mathbf {x} (s,t))\cdot \left({\partial \mathbf {x} \over \partial s}\times {\partial \mathbf {x} \over \partial t}\right)ds\,dt. } 
Krydsproduktet på højre side af dette udtryk er en overfladenormal, der er bestemt af parametriseringen.
Denne formel definerer integralet til venstre (bemærk punktet og vektornotationen for overfladeelementet).
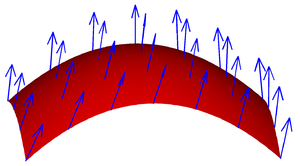
Et vektorfelt på en overflade.
Sætninger med overfladeintegraler
Forskellige nyttige resultater for overfladeintegraler kan udledes ved hjælp af differentialgeometri og vektorregning, f.eks. divergenssætningen og dens generalisering, Stokes' sætning.
Avancerede spørgsmål
Ændring af parametrisering
Ovenstående diskussion definerede overfladeintegralet ved hjælp af en parametrisering af overfladen S. En given overflade kan have flere parametriseringer. Når f.eks. nordpolens og sydpolens placering flyttes på en kugle, ændres bredde- og længdegraden for alle punkterne på kuglen. Et naturligt spørgsmål er så, om definitionen af overfladeintegralet afhænger af den valgte parametrisering. For integraler af skalarfelter er svaret på dette spørgsmål enkelt, idet værdien af overfladeintegralet vil være den samme uanset hvilken parametrisering man anvender.
Integraler af vektorfelter er mere komplicerede, fordi overfladenormalen er involveret. Matematikere har bevist, at givet to parametriseringer af den samme overflade, hvis overfladenormaler peger i samme retning, giver begge parametriseringer den samme værdi for overfladeintegralet. Hvis normalerne for disse parametriseringer imidlertid peger i modsatte retninger, er værdien af overfladeintegralet, der opnås ved hjælp af den ene parametrisering, det negative af den værdi, der opnås ved hjælp af den anden parametrisering. Det følger heraf, at vi, når vi har en overflade, ikke behøver at holde os til en entydig parametrisering; men når vi integrerer vektorfelter, er vi nødt til på forhånd at beslutte, hvilken retning normalen vil pege i, og derefter vælge en parametrisering, der er i overensstemmelse med denne retning.
Parametriseringer virker på dele af overfladen
Et andet problem er, at overflader nogle gange ikke har parametreringer, der dækker hele overfladen; dette gælder f.eks. for overfladen af en cylinder (med en endelig højde). Den indlysende løsning er så at dele overfladen op i flere stykker, beregne overfladeintegralet for hvert stykke og derefter lægge dem alle sammen sammen. Sådan fungerer det faktisk, men når man integrerer vektorfelter, skal man igen være omhyggelig med at vælge normalpunktsvektoren for hvert stykke af overfladen, så resultaterne er konsistente, når stykkerne sættes sammen igen. For cylinderen betyder det, at hvis vi beslutter, at for sideområdet skal normalen pege ud af kroppen, så skal normalen også pege ud af kroppen for den øverste og nederste cirkulære del for den øverste og nederste cirkulære del.
Uoverensstemmende overfladenormaler
Endelig findes der overflader, som ikke har en overfladenormal i hvert punkt med konsistente resultater (f.eks. Möbiusstriben). Hvis en sådan overflade deles i stykker, der vælges en parametrisering og en tilsvarende overfladenormal for hvert stykke, og stykkerne sættes sammen igen, kan de normalvektorer, der kommer fra forskellige stykker, ikke forenes. Det betyder, at der ved et eller andet kryds mellem to stykker vil være normalvektorer, der peger i modsatte retninger. En sådan overflade kaldes ikke-orienterbar. Vektorfelter kan ikke integreres på ikke-orienterbare overflader.
Relaterede sider
- Divergenssætning
- Stokes' sætning
- Linjeintegral
- Volumenintegral
- Kartesisk koordinatsystem
- Volumen- og overfladeelementer i et sfærisk koordinatsystem
- Volumen- og overfladeelementer i et cylindrisk koordinatsystem
- Holstein-Herring-metoden
Søge