Cylinder (geometri): Definition, formler, overflade og rumfang

Cylinder (geometri): definition, formler, overflade og rumfang — klare forklaringer, eksempler og beregninger for cirkulære og elliptiske cylindre.

Forfatter: Leandro Alegsa

01-02-2026 18:18

En cylinder er en af de mest grundlæggende buede tredimensionale geometriske former. Overfladen består af alle punkter i en fast afstand fra et bestemt linjestykke, kaldet cylinderens akse, og formen kan opfattes som et cirkulært prisme. Både overfladen og den faste form indeni kaldes ofte en cylinder. En cylinders overfladeareal og rumfang var kendt allerede i oldtiden og bruges stadig i mange praktiske beregninger.

I differentialgeometri defineres en cylinder mere generelt som en reguleret overflade, der er dannet ved en familie af parallelle linjer (generatricer) afhængig af én parameter. Hvis et tværsnit vinkelret på aksen er en cirkel, får man en cirkulær cylinder (ofte blot kaldet "cylinder"). Hvis tværsnittet er en ellipse, parabel eller hyperbel, taler man om henholdsvis en elliptisk cylinder, en parabolisk cylinder eller en hyperbolisk cylinder. Cylinderens generatricer er parallelle linjer, og en cylinder er et eksempel på en reguleret og udvikelbar overflade (dvs. den kan udfoldes til en flad flade uden stræk).

Terminologi og grundparametre

Aksen: det linjestykke som generatricerne er parallelle med.
Radius (r): afstanden fra aksen til et punkt på cirkelbasen (for cirkulær cylinder).
Højde (h): den korteste afstand mellem de to basisplaner, altså afstanden langs en linje vinkelret på baserne.
Generatricer: de parallelle linjer, der danner overfladen.
Tværsnit: snit med et plan vinkelret på aksen giver formen af basen (fx cirkel eller ellipse).

Formler for cirkulær cylinder (ret, lukkede)

Rumfang: V = A_base · h = π r² h.
Grundflade (en base): A_base = π r².
Sideareal / mantelareal: M = omkreds(base) · h = (2π r) · h = 2π r h.
Totalt overfladeareal (to baser + mantel): A_total = 2·π r² + 2π r h = 2π r (r + h).

Forklaring: mantelarealet findes ved at "udfolde" cylinderen — manteludviklingen er et rektangel med højde h og bredde lig med cirklens omkreds 2πr, derfor M = 2πrh. Rumfanget følger fra, at cylinderen kan betragtes som stakken af cirkulære tværsnit af areal πr² gennem højden h.

Åben cylinder og oblique (skæv) cylinder

En åben cylinder mangler en eller begge baser; så er det relevante overfladeareal kun mantelarealet eller mantel + én base.
For en skæv (oblique) cylinder er generatricerne stadig parallelle, men ikke vinkelrette på basisplanerne. Rumfangsformlen V = A_base · h gælder stadig, hvor h er den ortogonale højde (afstand mellem basisplanerne). Mantelarealet svarer til omkredsen af basen multipliceret med den ortogonale højde.

Elliptisk cylinder og andre baser

For en elliptisk cylinder med basisellipse semiakser a og b og højde h gælder:

Rumfang: V = A_base · h = (π a b) · h.
Mantelareal: M = (perimeter_ellipse) · h, hvor ellipsens omkreds har ingen simpel elementær lukket form — man anvender approximationer (fx Ramanujans formel).

Ramanujans approximation for ellipsens omkreds P er fx: P ≈ π (a + b) [1 + (3λ)/(10 + √(4 − 3λ))], hvor λ = ((a − b)/(a + b))².

Geometriske og differentialgeometriske egenskaber

Cylinderen er en ruled surface (en reguleret overflade) og udvikelbar (Gaussisk kurvatur = 0), hvilket betyder, at mantelens overflade kan udfoldes til et fladt rektangel uden distortion.
For en cirkulær cylinder er de to hovedkurvaturer κ1 = 0 (langs aksen) og κ2 = 1/r (tværs over cirklen). Middelkurvaturen er derfor H = 1/(2r).

Anvendelser og eksempler

Cylindere optræder i mange dagligdags og tekniske sammenhænge: beholdere (dåser), rør, søjler, motorstempler og flaskehalse. Beregninger af rumfang og overflade er vigtige ved materialeberegning, produktion og transport.

Eksempel: En lukket cirkulær cylinder har r = 5 cm og h = 10 cm. Rumfanget er V = π·5²·10 = 250π ≈ 785,4 cm³. Totalt overfladeareal er A = 2π·5·(5 + 10) = 2π·5·15 = 150π ≈ 471,2 cm².

Yderligere bemærkninger

En cylinder kan defineres algebraisk i R³ — fx en ret cirkulær cylinder med akse langs z-aksen og radius r er mængden {(x,y,z) | x² + y² = r²}.
Momentinertia (træghedsmoment) for en homogen massetæt cylinder af masse m og radius r omkring aksen: I_z = (1/2) m r². Om en diameter i tværsnitsplanet er I = (1/12) m (3r² + h²).
Ved numeriske beregninger: husk enheder (f.eks. cm³ for rumfang, cm² for areal) og nævn om cylinderen er åben eller lukket.

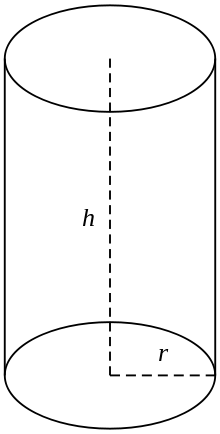
En ret cirkulær cylinder

Almindelig anvendelse

I almindelig brug forstås ved en cylinder et endeligt snit af en ret cirkelcylinder, dvs. cylinderen med de genererende linjer vinkelret på bundene, med enderne lukket til to cirkelflader, som i figuren (til højre). Hvis cylinderen har en radius $r$ og en længde (højde) h, er dens volumen givet ved:

$V$ $= πr h 2$

og dens overfladeareal er:

arealet af toppen ( $πr 2) +$
bundens areal ( $πr 2) +$
arealet af siden ( $2πrh$ ).

Uden top og bund (sideareal) er overfladearealet derfor:

$A$ $= 2πrh$ .

Med top og bund er overfladen:

$A$ $= 2πr 2 + 2πrh = 2πr (r + h)$ .

For et givet rumfang har cylinderen med det mindste overfladeareal $h = 2r$ . For et givet overfladeareal har cylinderen med det største rumfang $h = 2r,$ dvs. cylinderen passer ind i en terning (højde = diameter).

Bind

Med en ret cirkelformet cylinder med en højde $h$ enheder og en bund med radius $r$ enheder med koordinatakserne valgt således, at oprindelsen er i centrum af den ene bund og højden måles langs den positive x-akse. Et plant snit i en afstand af $x$ enheder fra oprindelsen har et areal på $A (x)$ kvadrat enheder, hvor

A ( x ) = π r 2 {\displaystyle A(x)=\pi r^{2}} $A(x)=\pi r^{2}$

eller

A ( y ) = π r 2 {\displaystyle A(y)=\pi r^{2}} $A(y)=\pi r^{2}$

Et volumenelement er en ret cylinder med et grundareal $Aw i$ kvadrat enheder og en tykkelse på $Δ i$ x enheder. Hvis V kubik enheder er rumfanget af den højre cirkulære cylinder, er der således tale om Riemanns summer,

V o l u m e af c y l i n d e r = lim | | | Δ → 0 | | | ∑ i = 1 n A ( w i ) Δ i x {\displaystyle \mathrm {Volume\;af\;cylinder} =\lim _{||\\Delta \til 0|||}\sum _{i=1}^{n}A(w_{i})\Delta _{i}x} $\mathrm {Volume\;of\;cylinder} =\lim _{||\Delta \to 0||}\sum _{i=1}^{n}A(w_{i})\Delta _{i}x$

= ∫ 0 h A ( y ) 2 d y {\displaystyle =\int _{0}^{h}A(y)^{2}\,dy} $=\int _{0}^{h}A(y)^{2}\,dy$

= ∫ 0 h π π r 2 d y {\displaystyle =\int _{0}^{h}\pi r^{2}\,dy} $=\int _{0}^{h}\pi r^{2}\,dy$

= π r 2 h {\displaystyle =\pi \,r^{2}\,h\,} $=\pi \,r^{2}\,h\,$

Ved hjælp af cylindriske koordinater kan volumenet beregnes ved integration over

= ∫ 0 h ∫ 0 2 π ∫ 0 r s d s d d d ϕ d z {\displaystyle =\int _{0}^{h}\int _{0}^{2\pi }\int _{0}^{r}s\,\,ds\,d\,d\phi \,dz} $=\int _{0}^{h}\int _{0}^{2\pi }\int _{0}^{r}s\,\,ds\,d\phi \,dz$

= π r 2 h {\displaystyle =\pi \,r^{2}\,h\,} $=\pi \,r^{2}\,h\,$

Cylindrisk snit

Cylindriske snit er skæringspunkterne mellem cylindre og planer. For en ret cirkulær cylinder er der fire muligheder. Et plan, der tangerer cylinderen, møder cylinderen i en enkelt lige linje. Flyves planen parallelt med sig selv, skærer den enten ikke cylinderen eller skærer den i to parallelle linjer. Alle andre planer skærer cylinderen i en ellipse eller, når de er vinkelret på cylinderens akse, i en cirkel.

Andre typer af cylindre

En elliptisk cylinder eller cylindroid er en kvadrisk overflade med følgende ligning i kartesiske koordinater:

( x a ) 2 + ( y b ) 2 = 1. {\displaystyle \left({\frac {x}{a}}\right)^{2}+\left({\frac {y}{b}}}\right)^{2}=1.} $\left({\frac {x}{a}}\right)^{2}+\left({\frac {y}{b}}\right)^{2}=1.$

Denne ligning gælder for en elliptisk cylinder, som er en generalisering af den almindelige cirkulære cylinder ( $a = b$ ). Endnu mere generel er den generaliserede cylinder: tværsnittet kan være en hvilken som helst kurve.

Cylinderen er en degenereret kvadratur, fordi mindst en af koordinaterne (i dette tilfælde $z$ ) ikke indgår i ligningen.

En skrå cylinder har en over- og underside, der er forskudt fra hinanden.

Der findes andre mere usædvanlige typer af cylindre. Det er de imaginære elliptiske cylindre:

( x a ) 2 + ( y b ) 2 = - 1 {\displaystyle \left({\frac {x}{a}}\right)^{2}+\left({\frac {y}{b}}}\right)^{2}=-1} $\left({\frac {x}{a}}\right)^{2}+\left({\frac {y}{b}}\right)^{2}=-1$

den hyperboliske cylinder:

( x a ) 2 - ( y b ) 2 = 1 {\displaystyle \left({\frac {x}{a}}\right)^{2}-\left({\frac {y}{b}}}\right)^{2}=1} $\left({\frac {x}{a}}\right)^{2}-\left({\frac {y}{b}}\right)^{2}=1$

og den paraboliske cylinder:

x 2 + 2 a y = 0. {\displaystyle x^{2}+2ay=0.\,} $x^{2}+2ay=0.\,$

↑"MathWorld: Cylindrisk snit".

En elliptisk cylinder

I projektiv geometri er en cylinder simpelthen en kegle, hvis spids er i uendelighed, hvilket visuelt svarer til en cylinder i perspektiv, der ser ud til at være en kegle mod himlen.

Spørgsmål og svar

Q: Hvad er en cylinder?

A: En cylinder er en tredimensionel geometrisk form, hvis overflade er dannet af punkter i en fast afstand fra et bestemt linjestykke, kendt som cylinderens akse. Den kan opfattes som et cirkulært prisme, og både overfladen og den faste form, der skabes indeni, kan kaldes en cylinder.

Spørgsmål: Hvor længe har man kendt til cylinders overfladeareal og volumen?

Svar: Cylinders overfladeareal og volumen har været kendt siden oldtiden.

Spørgsmål: Hvad er elliptiske, paraboliske og hyperboliske cylindre?

A: Elliptiske, paraboliske og hyperboliske cylindre er cylindre, hvis tværsnit er henholdsvis en ellipse, parabel eller hyperbel.

Sp: Hvordan defineres en cylinder i differentialgeometri?

Svar: I differentialgeometri defineres en cylinder mere bredt som en reguleret overflade, der er dækket af en familie af parallelle linjer med én parameter.

Spørgsmål: Hvad betyder det, at noget er "reguleret"?

A: At være "reguleret" betyder, at der på en eller anden måde er tegnet lige linjer på det.

Spørgsmål: Er der kun én type cylinder?

A: Nej, der findes mange forskellige typer af cylindre, f.eks. elliptiske, paraboliske og hyperboliske cylindre, som alle har forskellige tværsnit.

Søge