Eulers formel (e^{ix}=cos x + i sin x) — definition og anvendelser

Eulers formel (e^{ix}=cos x+i sin x) — klar definition, historisk kontekst og praktiske anvendelser i kompleks analyse samt forbindelsen mellem trigonometriske og eksponentielle funktioner.

Inden for kompleks analyse er Eulers formel, også kaldet Eulers relation, en ligning, der forbinder komplekse tal og trigonometriske funktioner. Den siger, at for et reelt tal x gælder

e i x = cos x + i sin x {\displaystyle e^{ix}=\cos x+i\sin x}

Her er e Eulers tal, og i er den imaginære enhed. Forholdet forbinder altså den eksponentielle funktion med cosinus og sinus, og det giver et naturligt link mellem algebraiske og geometriske beskrivelser af komplekse tal: den komplekse eksponentialfunktion beskriver en enhedscirkel i det komplekse plan.

Hvordan kan man forstå eller bevise formlen?

• Via potensrækker (Taylor-serier): De reelle funktioner har udvidelser omkring 0,
  e^x = sum_{n=0}^\infty x^n/n!, cos x = sum_{n=0}^\infty (-1)^n x^{2n}/(2n)!, sin x = sum_{n=0}^\infty (-1)^n x^{2n+1}/(2n+1)!. Ved at indsætte x -> i x i e^x‑rækken og bruge i^{2n}=(-1)^n får man præcis cos x + i sin x.
• Via differentialligninger: Funktionen f(x)=e^{ix} opfylder f'(x)=i f(x) med f(0)=1. Den komplekse funktion cos x + i sin x opfylder samme differentialligning og samme begyndelsesværdi, så de er identiske (unik løsning af begyndelsesværdiproblemet).
• Via analytisk continuation: Eulers oprindelige udsagn gjaldt for reelle vinkler, men ved at betragte de analytiske udvidelser (komplekse variable) ser man, at identiteten også gælder for komplekse værdier af x.

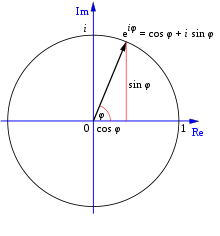
Geometrisk tolkning

Eulers formel siger, at multiplikation med e^{iθ} svarer til en rotation i det komplekse plan med vinkel θ omkring origo. Derfor har e^{iθ} absolut værdi 1 og argument θ. Dette fører naturligt til polær form af et komplekst tal: ethvert ikke-nul z kan skrives som

z = r e^{iθ}, hvor r = |z| og θ = arg(z).

Væsentlige egenskaber og identiteter

• Real- og imaginære dele: cos x = (e^{ix}+e^{-ix})/2 og sin x = (e^{ix}-e^{-ix})/(2i).
• De Moivres formel: (cos x + i sin x)^n = cos(nx) + i sin(nx) for heltal n, som følger direkte fra e^{inx} = (e^{ix})^n.
• Periode: e^{i(x+2π)} = e^{ix}, da π {\displaystyle \pi } og 2 π {\displaystyle 2\pi } giver bl.a.
• Eksempler: e i π = - 1 {\displaystyle e^{i\pi }=-1} og e i 2 π = 1 {\displaystyle e^{i2\pi }=1} .

Euler-identiteten

Et særligt velkendt tilfælde er e^{iπ} + 1 = 0, ofte kaldet Euler‑identiteten. Den forbinder fem fundamentale konstanter: 0, 1, π, e og i, i én enkel ligning og opfattes ofte som et smukt eksempel på matematikens indre sammenhæng.

Anvendelser

• Frekvensanalyse og Fourier-transform: Komplekse eksponentialer er grundlaget for Fourier-serier og Fourier-transformer, som omsætter mellem tids-/rumdomænet og frekvensdomænet i signalbehandling og fysik.
• Fasorer i elektroteknik: Vekselstrømsanalyse bruger e^{iωt} til at repræsentere sinusformede spændinger og strømme, hvilket forenkler beregninger med faseforskydninger og impedanser.
• Løsning af differentialligninger: Eksponentielle løsninger med komplekse argumenter forekommer naturligt i lineære differentialligninger med konstante koefficienter og giver oscillationsløsninger via reelle og imaginære dele.
• Forenkling af trigonometriske identiteter: Omformning til eksponentiel form gør mange trigonometriske beregninger og integrationer mere entydige og lettere at håndtere.
• Kompleks potentialteori og bølgeteori: Metoder med komplekse eksponentialer anvendes i analytisk funktionsteori, bølge- og kvantemekanik.

Udvidelser og bemærkninger

• Komplekse vinkler: Formlen gælder også når x er komplekst: for z∈C har e^{iz} = cos z + i sin z, hvor cos og sin forstås som de analytiske udvidelser.
• Logaritme og flerværdighed: Når man går den anden vej og skriver θ = Arg(z) = -i log(z), bliver log(z) flerværdig fordi argumentet kan tilføjes 2kπ. Derfor er e^{iθ} mange-til-en: e^{i(θ+2kπ)} = e^{iθ}.
• Algebraisk brug: Polæreksponentialformen z = r e^{iθ} er nyttig ved multiplikation og division af komplekse tal: z1 z2 = r1 r2 e^{i(θ1+θ2)}.

Kort bevis via potensrækker (skematisk)

Udgangspunkt:

• e^{ix} = sum_{n=0}^\infty (ix)^n/n! = sum_{n=0}^\infty i^{2n} x^{2n}/(2n)! + sum_{n=0}^\infty i^{2n+1} x^{2n+1}/(2n+1)!.
• Brug i^{2n}=(-1)^n og i^{2n+1}=(-1)^n i, hvilket giver netop cos x + i sin x.

Samlet giver dette en kompakt og praktisk måde at arbejde med trigonometriske funktioner i mange grene af matematik og anvendt videnskab.

Spørgsmål og svar

Spørgsmål: Hvad er Eulers formel?

Sp: Hvem udgav Eulers formel?

Spørgsmål: Virker formlen, når vinklen ikke er et reelt tal?

Spørgsmål: Hvad sker der, når vinklen er pi?

Spørgsmål: Hvad sker der, når vinklen er 2pi?

Spørgsmål: Hvad repræsenterer "e" i denne ligning?

Spørgsmål: Hvad repræsenterer "i" i denne ligning?

Søg efter bogstav