Minkowski-rumtiden: 4-dimensionel rumtid i specielle relativitetsteori

Minkowski-rumtiden: Introduktion til 4-dimensionel rumtid i specielle relativitetsteori — struktur, metrisk signatur (-+++) og betydning for tid og bevægelse.

Forfatter: Leandro Alegsa

I den specielle relativitetsteori er Minkowski-rumtiden en firedimensional manifold, som blev skabt af Hermann Minkowski. Den har fire dimensioner: tre rumdimensioner (x, y, z) og en tidsdimension. Minkowski-rumtiden har en metrisk signatur på (-+++) og beskriver en flad overflade, når der ikke er nogen masse til stede. Konventionen i denne artikel er at kalde Minkowski-rumtid blot rumtid.

Minkowski-rumtiden gælder dog kun i den specielle relativitetsteori. I den generelle relativitetsteori anvendes begrebet krum rumtid til at beskrive virkningerne af tyngdekraften og accelereret bevægelse.


 

Grundlæggende struktur og metrisk tensor

Minkowski-rumtiden beskrives matematisk ved en metrisk tensor, ofte kaldet Minkowski-metrikken η. I de mest almindelige enheder (med lysets hastighed c eksplicit) skrives det kvadratiske interval mellem to nærliggende begivenheder som

ds² = -c² dt² + dx² + dy² + dz².

Med indeksnotation og enheder hvor c = 1 skrives metrikken som ημν = diag(-1, 1, 1, 1). Denne metrik bestemmer afstande i rumtiden og er ansvarlig for signaturen (-+++), der adskiller tidskomponenten fra de rumlige komponenter.

Invarians og Lorentz-transformationer

Det vigtigste kendetegn ved Minkowski-rumtiden er, at det kvadratiske interval ds² er invariant under Lorentz-transformationer. Det betyder, at alle inertialsystemer (observatører i lige linje og konstant fart) vil måle samme værdier af ds² mellem to begivenheder, selvom de måler forskellige tids- og rumkomponenter. Standardformen af en Lorentz-transformation i én rumdimension er

x' = γ (x - v t),
t' = γ (t - v x / c²),

hvor γ = 1 / sqrt(1 - v²/c²) er Lorentz-faktoren. Bevarelsen af ds² sikrer bl.a. bevarelse af årsagsforhold (kausalitet) og af lysets hastighed i vakuum.

Kausestruktur: lysets kegle og typer af intervaller

Ved at undersøge ds² kan man klassificere forholdet mellem to begivenheder:

  • Tidsskabende (timelike): ds² < 0. Begivenheder kan være forbundet af et objekt med farten < c; de kan påvirke hinanden og der findes en inertial observatør, der ser dem på samme sted i rum.
  • Lysskabende (lightlike / null): ds² = 0. Forbindelsen sker med lysets hastighed; grænsefladen for hvad der kan påvirke hvad kaldes lysets kegle (light cone).
  • Rumskabende (spacelike): ds² > 0. Begivenheder kan ikke være årsagssammenhængende (kræver superluminal hastighed), og simultanitet afhænger af observatørens bevægelsestilstand.

Lysets kegle deler rumtiden i fortid, fremtid og 'andetsteds' (hændelser, der er rumskabte i forhold til en given begivenhed). Dette er centralt for forståelsen af, hvad der kan påvirke hvad i relativitetsteorien.

Worldlines, egen-tid og målelige effekter

En objekts bane gennem rumtiden kaldes en worldline. For et tidslignende forløb er egen-tiden τ den tid, et ur måler langs worldlinen, givet ved

dτ² = -ds² / c² = dt² - (dx² + dy² + dz²)/c².

Egen-tid er en invariabel størrelse og svarer til den fysiske tid målt af en observatør, der bevæger sig sammen med objektet. Fra denne formel følger kendte fænomener som tidsdilatation (bevægelige ure går langsommere set fra en anden inertial observatør) og længdekontraktion (objekters længde i bevægelse er kortere i bevægelsesretningen):

Δt = γ Δτ (tidsdilatation),
L = L₀ / γ (længdekontraktion),

hvor L₀ er egenlængden (målt i objektets hvilesystem).

Fire-vektorer og fysikkens formulering

Minkowski-rumtiden gør det naturligt at formulere fysik i termer af fire-vektorer og tensorer, som transformerer på en simpel måde under Lorentz-gruppen. Eksempler:

  • Fire-position: xμ = (ct, x, y, z)
  • Fire-hastighed (4-velocity): uμ = dxμ/dτ
  • Energi-impuls-tensor og fire-impuls pμ = (E/c, p)

Denne formulering er praktisk ved relativistiske beregninger af bevægelse, kollisioner og bevarelser (energi, impulsmoment) og ligger tæt op ad den matematiske struktur i den generelle relativitetsteori.

Historisk betydning og relation til generel relativitet

Hermann Minkowskis indsigt i at kombinere tid og rum til én geometrisk enhed var et afgørende skridt for tolkningen af Einsteins specielle relativitet. Minkowskis rumtid er flad (nul rumtidskrumning) og beskriver universet i fravær af tyngdefelter. Når masse-energi tilføjes, bliver rumtiden krum, og man overgår til den generelle relativitetsteori, hvor metrikken ikke længere er Minkowskis simple diag(-1,1,1,1), men en løsning af Einsteins feltligninger.

Anvendelser og visualisering

Minkowski-diagrammer (rumtidstegninger) er et nyttigt pædagogisk værktøj til at visualisere worldlines, lyskepler og simultanitet. Minkowski-rumtiden er også grundlaget for moderne formuleringer af kvantefeltteori i flad rumtid og for forståelse af partikelkinematik ved relativistiske hastigheder.

Sammenfatning

Minkowski-rumtiden er den flade, firedimensionale rumtidsgeometri, der ligger til grund for specielle relativitetsteori. Den introducerer et invariants afstandsmål mellem begivenheder (ds²), definerer kausal struktur gennem lysets kegle, og gør det muligt at formulere fysik i formelt elegante fire-dimensionale variable. Når tyngdekraften indføres, generaliseres denne flade geometri til en krum rumtid i den generelle relativitetsteori.

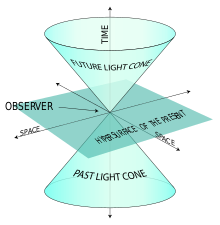
Eksempel på en lyskegle.  Zoom
Eksempel på en lyskegle.  

Definition(er)

Matematisk

Rumtiden kan opfattes som et firedimensionelt koordinatsystem, hvor akserne er givet ved

( c t , x , y , z ) {\displaystyle (ct,x,y,z)} {\displaystyle (ct,x,y,z)}

De kan også betegnes med

( x 1 , x 2 , x 3 , x 4 ) {\displaystyle (x_{1},x_{2},x_{3},x_{4})} {\displaystyle (x_{1},x_{2},x_{3},x_{4})}

Hvor x 1 {\displaystyle x_{1}}}{\displaystyle x_{1}} repræsenterer c t {\displaystyle ct}{\displaystyle ct} . Grunden til, at tiden måles i enheder af lysets hastighed gange tidskoordinaten, er, at tidsenhederne er de samme som rumenhederne. Rumtiden har differentialet for buelængde givet ved

d s 2 = - c 2 d t 2 + d x 2 + d y 2 + d z 2 {\displaystyle ds^{2}=-c^{2}dt^{2}+dx^{2}+dy^{2}+dz^{2}}+dz^{2}} {\displaystyle ds^{2}=-c^{2}dt^{2}+dx^{2}+dy^{2}+dz^{2}}

Dette indebærer, at rumtiden har en metrisk tensor givet ved

g u v = [ - 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 ] {\displaystyle g_{uv}={\begin{bmatrix}-1&0&0&0&0\\0&1&0&0&0&0&0&1&0&0&0&0&1\end{bmatrix}}} {\displaystyle g_{uv}={\begin{bmatrix}-1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{bmatrix}}}

Som tidligere nævnt er rumtiden flad overalt; til en vis grad kan den opfattes som et plan.

Enkel

Rumtiden kan opfattes som den "arena", hvor alle begivenheder i universet finder sted. Det eneste, man behøver for at specificere et punkt i rumtiden, er et bestemt tidspunkt og en typisk rumlig orientering. Det er svært (næsten umuligt) at visualisere fire dimensioner, men man kan lave en vis analogi ved hjælp af nedenstående metode.



 

Rumtidsdiagrammer

Hermann Minkowski introducerede en bestemt metode til grafisk fremstilling af koordinatsystemer i Minkowskis rumtid. Som det ses til højre, vil forskellige koordinatsystemer være uenige om et objekts rumlige orientering og/eller position i tiden. Som det fremgår af diagrammet, er der kun én rumlig akse (x-aksen) og én tidsakse (ct-aksen). Om nødvendigt kan man indføre en ekstra rumlig dimension (y-aksen); desværre er dette grænsen for antallet af dimensioner: det er umuligt at lave grafer i fire dimensioner. Reglen for grafering i Minkowski-rumtid er følgende:

1) Vinklen mellem x-aksen og x'-aksen er givet ved t a n ( α ) = v c {\displaystyle tan(\alpha )={\frac {v}{c}}}}}{\displaystyle tan(\alpha )={\frac {v}{c}}} hvor v er objektets hastighed

2) Lysets hastighed gennem rumtiden danner altid en vinkel på 45 grader med begge akser.



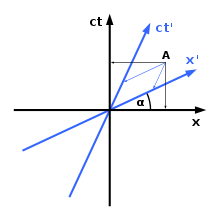
 I relativitetsteorien henfører begge observatører begivenheden i A til forskellige tidspunkter.  Zoom
I relativitetsteorien henfører begge observatører begivenheden i A til forskellige tidspunkter.  

Rumtiden i den generelle relativitetsteori

I den generelle relativitetsteori brugte Einstein ligningen

G m v = 8 π G T m v {\displaystyle \mathbb {G} _{mv}=8\pi {\mathcal {G}}}\mathbb {T} _{mv}} {\displaystyle \mathbb {G} _{mv}=8\pi {\mathcal {G}}\mathbb {T} _{mv}}

For at rumtiden faktisk kan krumme sig; de resulterende virkninger er tyngdekraftens virkninger.



 

Relaterede sider

Myndighedskontrol: Nationalbiblioteker Edit this at Wikidata
  • Frankrig (data)
  • Tyskland
  • USA
  • Letland
  • Tjekkiet


 

Spørgsmål og svar

Spørgsmål: Hvad er Minkowski-rumtid?


A: Minkowski-rumtid er en firedimensional manifold skabt af Hermann Minkowski. Den har tre rumdimensioner (x, y, z) og en tidsdimension.

Sp: Hvad er den metriske signatur af Minkowski-rumtiden?


Svar: Den metriske signatur for Minkowski-rumtiden er (-+++).

Spørgsmål: Hvordan beskriver Minkowski-rumtiden en flad overflade?


Svar: Når der ikke er nogen masse til stede, beskriver Minkowski rumtid en flad overflade.

Spørgsmål: Gælder Minkowski-rumtid for den generelle relativitetsteori?


Svar: Nej, Minkowski rumtid gælder kun i den specielle relativitetsteori. Den generelle relativitetsteori bruger begrebet krum rumtid til at beskrive virkningerne af tyngdekraften og accelereret bevægelse.

Spørgsmål: Hvor mange dimensioner har Minkowsi rumtid?


Svar: Minkowsi rumtid har fire dimensioner - tre rumdimensioner (x, y, z) og en tidsdimension.

Spørgsmål: Hvem skabte begrebet Minkowsi rumtid?


Svar: Hermann Minkowksi skabte begrebet MInkowski rumtid.


Søge
AlegsaOnline.com - 2020 / 2025 - License CC3