Tegn (matematik)
I matematik henviser ordet tegn til den egenskab, at det er positivt eller negativt. Alle reelle tal (som ikke er nul) er enten positive eller negative og har derfor et tegn. Nul i sig selv er uden tegn, eller tegnløst. Ud over at sætte tegn på reelle tal bruges ordet tegn i hele matematikken til at angive dele af matematiske objekter, der betyder positivitet og negativitet. Normalt betragtes tal, hvis de ses uden tegn, som et positivt tal.
Ordet tegn bruges også nogle gange om forskellige matematiske tegn, f.eks. plus- og minustegn og multiplikationstegn.

Plus- og minussymbolerne bruges til at vise et tals fortegn. Plus betyder positivt, og minus betyder negativt.
Tegn på et tal
Et reelt tal er positivt, hvis det er større end nul, og negativt, hvis det er mindre end nul. Egenskaben ved at være positiv eller negativ kaldes talets fortegn. Nul i sig selv anses ikke for at have et fortegn.
I aritmetik angives et tals fortegn ofte ved at sætte et plus- eller minustegn foran tallet. F.eks. vil +3 angive et positivt 3, og -3 vil angive et negativt 3. Når der ikke er angivet noget plus- eller minustegn, er den vigtigste måde at se det på, at et tal er positivt.
Fortegn for ethvert tal, der ikke er nul, kan ændres til positivt ved hjælp af absolutte værdi-funktionen. F.eks. er den absolutte værdi af -3 og den absolutte værdi af 3 begge lig med 3. I symboler vil dette blive skrevet |-3| = 3 og |3| = 3.
Tegn på nul
Tallet nul er hverken positivt eller negativt og har derfor intet fortegn. I aritmetik betyder +0 og -0 begge det samme tal 0.
Betydninger af tegn
Da nul hverken er positivt eller negativt, bruges følgende undertiden til at angive et ukendt tals fortegn:
- Et tal er positivt, hvis det er større end nul.
- Et tal er negativt, hvis det er mindre end nul.
- Et tal er ikke-negativt, hvis det er større end eller lig med nul.
- Et tal er ikke positivt, hvis det er mindre end eller lig med nul.
Et ikke-negativt tal er således enten positivt eller nul, mens et ikke-positivt tal er enten negativt eller nul. F.eks. er den absolutte værdi af et reelt tal altid ikke-negativ, men er ikke nødvendigvis positiv.
Den samme definition bruges undertiden for funktioner, der tager reelle eller hele talværdier. En funktion kaldes f.eks. positiv, hvis alle dens værdier er positive, eller ikke-negativ, hvis alle dens værdier er ikke-negative.
Tegnet på en vinkel
I mange tekster er det almindeligt at se et tegn sammen med et mål for en vinkel, især en lokaliseret vinkel eller en rotationsvinkel. I en sådan situation siger tegnet, om vinklen er i urets retning eller mod urets retning. Selv om der kan anvendes forskellige konventioner, er det i matematikken almindeligt, at vinkler mod uret tæller som positive, og vinkler med uret tæller som negative.
Det er også muligt at sætte et tegn på en drejningsvinkel i tre dimensioner, hvis man antager, at drejeaksen er blevet orienteret. Specifikt tæller en højredrejning omkring en akse normalt som positiv, mens en venstredrejning tæller som negativ.
Tegn på en retning
I aritmetik og fysik er det almindeligt at betegne visse retninger som positive eller negative. Som et grundlæggende eksempel tegnes tallinjen normalt med positive tal til højre og negative tal til venstre:
![]()
I det kartesiske plan opfattes retningen mod højre og opad normalt som positive, idet retningen mod højre er den positive x-retning og retningen opad er den positive y-retning.
Andre betydninger
Ud over tegnet for et reelt tal bruges ordet tegn også på forskellige beslægtede måder i matematik og videnskaberne:
- I grafteori er en signeret graf en graf, hvor hver kant er markeret med et positivt eller negativt tegn.
- I fysik er enhver elektrisk ladning forsynet med et tegn, enten positivt eller negativt. Ifølge de generelle regler er en positiv ladning en ladning med samme fortegn som en proton, og en negativ ladning er en ladning med samme fortegn som en elektron.
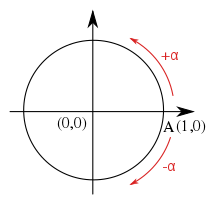
Målt fra x-aksen er vinkler på enhedscirklen positive mod uret og negative med uret.
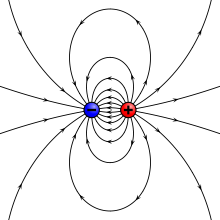
Elektrisk ladning kan være positiv eller negativ.
Søge