Heisenbergs usikkerhedsprincip | de vigtigste resultater af det tyvende århundredes fysik

Forvirring med observatørvirkning

Historisk set er usikkerhedsprincippet blevet forvekslet med en noget lignende effekt i fysikken, som kaldes observatørvirkningen. Denne siger, at målinger af nogle systemer ikke kan foretages uden at påvirke systemerne. Heisenberg tilbød en sådan observatør-effekt på kvanteplan som en fysisk "forklaring" på kvanteusikkerheden.

Men det er nu klart, at usikkerhedsprincippet er en egenskab ved alle bølgelignende systemer. Det opstår i kvantemekanikken simpelthen på grund af alle kvanteobjekters materie-bølgenatur. Usikkerhedsprincippet angiver således faktisk en grundlæggende egenskab ved kvantesystemer og er ikke et udsagn om den nuværende teknologis observationelle succes. "Måling" betyder ikke kun en proces, som en fysikobservatør deltager i, men derimod enhver vekselvirkning mellem klassiske og kvanteobjekter uanset en observatør.

 

Idéen om ubestemthed

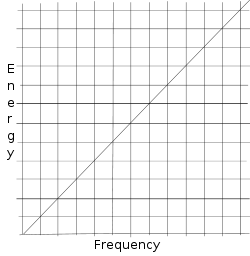
Usikkerhedsprincippet stammer fra Werner Heisenbergs matrixmekanik. Max Planck vidste allerede, at energien af en lysenhed er proportional med frekvensen af denne lysenhed ( E ∝ ν {\displaystyle E\propto \nu } ), og at dens energimængde kan udtrykkes i velkendte termer som joule ved hjælp af en proportionalitetskonstant. Den konstant, han gav verden, kaldes nu Planck-konstanten og repræsenteres af bogstavet h. Når matricer bruges til at udtrykke kvantemekanikken, skal to matricer ofte multipliceres for at få en tredje matrix, der giver det svar, som fysikeren forsøger at finde. Men multiplikation af en matrix som P (for impuls) med en matrix som X (for position) giver en anden svarmatrix end den, man får, når man multiplicerer X med P. Resultatet af at multiplicere P med X og X med P og derefter sammenligne dem, omfatter altid Planck-konstanten som en faktor. Det tal, der anvendes til at skrive Planck-konstanten, vil altid afhænge af det anvendte målesystem. (Med et bestemt målesystem er dens numeriske værdi 1.) Hældningen af linjen i diagrammet til højre, der viser forholdet mellem frekvens og energi, vil også afhænge af det valgte målesystem.

De følgende diagrammer viser, hvad der sker, når vi forsøger at måle både sted og impuls.

Det praktiske resultat af denne matematiske opdagelse er, at når en fysiker gør positionen mere tydelig, så bliver momentum mindre tydeligt, og når fysikeren gør momentum mere tydeligt, så bliver positionen mindre tydeligt. Heisenberg sagde, at tingene er "ubestemte", og andre mennesker kunne lide at sige, at de var "usikre". Men matematikken viser, at det er tingene i verden, der er ubestemte eller "uklare", og ikke at det blot er mennesker, der er usikre på, hvad der foregår.

 
Ved at hænge det midterste mellemrum op med fjedre kan impulsen måles, men det er uforudsigeligt at flytte mellemrummet, så information om fotonens placering i midten går tabt.  


Fjedermonteret hul måler momentum  


Smalt hul, diffust fokus  


Ved at indsnævre afstanden øges sikkerheden for, hvor fotonen befinder sig i midten, men dens retning derfra til detektionsskærmen til højre bliver tilsvarende mere usikker.  


Stort hul, skarpt fokus  



 

Ubestemthed i matematisk form

Her vil vi vise den første ligning, der gav den grundlæggende idé, som senere blev vist i Heisenbergs usikkerhedsprincip.

Heisenbergs banebrydende artikel fra 1925 bruger ikke og nævner ikke engang matricer. Heisenbergs store succes var "det system, som i princippet var i stand til entydigt at bestemme de relevante fysiske kvaliteter (overgangsfrekvenser og amplituder)" af brintstråling.

Efter at Heisenberg havde skrevet sin gennembrudspapir, gav han den til en af sine lærere til at rette op på den og tog på ferie. Max Born blev forundret over ligningerne og de ikke-kommuterende ligninger, som selv Heisenberg mente var et problem. Efter flere dage Born indså, at disse ligninger var retninger for at skrive ud matricer. Matricer var nye og mærkelige, selv for matematikere på den tid, men hvordan man laver matematik med dem var allerede klart kendt. Han og et par andre arbejdede alt ud i matrixform, inden Heisenberg kom tilbage fra sin ferie, og i løbet af få måneder gav den nye kvantemekanik i matrixform dem grundlaget for endnu et papir.

Max Born så, at når de matricer, der repræsenterer pq og qp, blev beregnet, ville de ikke være lige store. Heisenberg havde allerede set det samme i forbindelse med sin oprindelige måde at skrive tingene på, og Heisenberg kan have gættet, hvad der næsten øjeblikkeligt var indlysende for Born - at forskellen mellem svarmatricerne for pq og qp altid ville involvere to faktorer, der kom fra Heisenbergs oprindelige matematik: Plancks konstant h og i, som er kvadratroden af negativ 1. Så selve ideen om det, som Heisenberg foretrak at kalde "ubestemthedsprincippet" (normalt kendt som usikkerhedsprincippet), gemte sig i Heisenbergs oprindelige ligninger.

Heisenberg havde undersøgt de ændringer, der sker i et atom, når en elektron ændrer sit energiniveau og dermed kommer tættere på atomets centrum eller længere væk fra dets centrum, og især situationer, hvor en elektron falder til en lavere energitilstand i to trin. Max Born forklarede, hvordan han tog Heisenbergs mærkelige "opskrift" til at finde produktet, C, af en ændring i et atom fra energiniveau n til energiniveau n-b, som involverede at tage summen af multiplikationen af en ændring i noget, der kaldes A (som f.eks. kunne være frekvensen af en foton), der er produceret af en ændring af energien af en elektron i atomet mellem energitilstand n og energitilstand n-a) med en efterfølgende ændring i noget, der kaldes B (som f.eks. kunne være amplituden af en ændring), der er produceret af en anden ændring i energitilstand fra n-a til n-b):

C ( n , n - b ) = ∑ a A ( n , n - a ) B ( n - a , n - b ) {\displaystyle C(n,n-b)=\sum _{a}^{}\}\,A(n,n-a)B(n-a,n-b)}

og opdagede noget banebrydende:

Ved at overveje ...eksempler...[Heisenberg] fandt denne regel.... Dette var i sommeren 1925. Heisenberg...tog orlov...og overdrog mig sit papir til offentliggørelse....

Heisenbergs multiplikationsregel gav mig ingen ro, og efter en uges intensivt eftertænke og afprøvning kom jeg pludselig i tanke om en algebraisk teori.... Sådanne kvadratiske arrays er ganske velkendte for matematikere og kaldes matricer, i forbindelse med en bestemt multiplikationsregel. Jeg anvendte denne regel på Heisenbergs kvantebetingelse og fandt, at den stemte overens for de diagonale elementer. Det var let at gætte, hvad de resterende elementer måtte være, nemlig nul; og straks stod der foran mig den mærkelige formel

Q P - P Q = i h 2 π {\displaystyle {QP-PQ={\frac {ih}{2\pi }}}}
 [Symbolet Q er matrixen for forskydning, P er matrixen for impuls, i står for kvadratroden af negativ et, og h er Plancks konstant].

Senere omsatte Heisenberg sin opdagelse til en anden matematisk form:

Δ x Δ p ≥ ℏ 2 {\displaystyle \Delta x\,\Delta p\geq {\frac {\hbar }{2}}}}

(Det specielle symbol ℏ {\displaystyle {\hbar }} kaldes "h-bar" eller "reduceret Planks-konstant" og er lig med h 2 π {\displaystyle {\frac {h}{2\pi }}} .)

Matematikken er en måde at beskrive ting, der sker i den virkelige verden. Man kunne forestille sig, at det ville være let at få både den nøjagtige position af noget og dets nøjagtige masse, bane og hastighed på samme tid. Men i virkeligheden skal du gøre to ting for at få dit svar. Hvis du måler positionen og bevægelsesmængden af en kugle, der sidder fast i en klippe på et stort bjerg et eller andet sted, er det en simpel sag. Bjerget ser ikke ud til at bevæge sig nogen steder hen, og det gør kuglen heller ikke. Så dens position er kendt, og dens hastighed er 0, så dens impuls er også 0. Men hvis kuglen befinder sig et sted mellem et gevær og et mål, vil det være svært at få dens position på et givet tidspunkt. Det bedste, vi kan gøre, er at tage et billede af den ved hjælp af et kamera med en meget hurtig lukker. Men et enkelt tryk på lukkeren vil kun give én ting, nemlig kuglens position på tidspunktet t. For at få momentummet kan vi måske lægge en paraffinblok i vejen for kuglen og måle, hvordan paraffinblokken bevægede sig, da den stoppede kuglen. Eller, hvis vi kendte kuglens masse, kunne vi tage en sekvens af to billeder og beregne hastigheden ved at kende forskellen mellem kuglens to positioner og tiden mellem dens to optrædener. Uanset hvordan vi gør det, er vi nødt til at måle masse og position og tid mellem to fremvisninger. Vi ender med at foretage mindst to målinger for at nå frem til x og p. I så fald må vi vælge, hvilken måling vi vil foretage først og hvilken vi vil foretage derefter. Det ser ud til at være ligegyldigt, hvilken rækkefølge vores målinger foretages i. At måle kuglens masse og derefter måle dens positioner to gange, eller at måle kuglens positioner to gange og derefter genfinde kuglen og måle dens masse ville ikke gøre nogen forskel, vel? Vi har trods alt ikke gjort noget ved kuglen, når vi vejer den, eller når vi tager billeder af den.

På den meget lille skala, når vi måler noget som en elektron, gør hver måling imidlertid noget ved den. Hvis vi først måler positionen, ændrer vi dens momemtum i processen. Hvis vi måler elektronens momentum først, ændrer vi dens position i processen. Vores håb ville være at måle det ene og derefter måle det andet, før der sker en ændring, men selve vores måling medfører en ændring, og det bedste, vi kan håbe på, er at reducere den energi, vi bidrager til elektronen ved at måle den, til et minimum. Denne minimumsenergimængde har Planck-konstanten som en af sine faktorer.

 

Usikkerhed går ud over matrixmatematik

Heisenbergs usikkerhedsprincip blev fundet i de tidligste ligninger i den "nye" kvantefysik, og teorien blev givet ved hjælp af matrixmatematik. Usikkerhedsprincippet er imidlertid et faktum om naturen, og det dukker op i andre måder at tale om kvantefysik på, f.eks. i Erwin Schrödingers ligninger.

 

Ubestemthed i naturen, ikke menneskers usikkerhed

Der har været to meget forskellige måder at se på Heisenbergs opdagelse på: Nogle mennesker mener, at de ting, der sker i naturen, er "determinerede", dvs. at tingene sker efter en bestemt regel, og hvis vi kunne vide alt, hvad vi behøver at vide, kunne vi altid sige, hvad der vil ske næste gang. Andre mener, at de ting, der sker i naturen, kun er styret af sandsynlighed, og at vi kun kan vide, hvordan tingene vil opføre sig i gennemsnit - men det ved vi meget præcist.

Fysikeren John Stewart Bell fandt en måde at bevise, at den første måde ikke kan være korrekt. Hans arbejde kaldes Bell's teorem eller Bell's ulighed.

 

Populær kultur

Udtrykket "kvantespring" eller "kvantespring" er blevet opfattet som udtryk for en stor og transformativ forandring, og det bruges ofte i hyperbolske vendinger af politikere og i salgskampagner i massemedierne. I kvantemekanikken bruges det til at beskrive en elektrons overgang fra en bane omkring atomets kerne til en hvilken som helst anden bane, højere eller lavere.

Nogle gange bruges ordet "quantum" i navnene på kommercielle produkter og virksomheder. Briggs and Stratton fremstiller f.eks. mange forskellige slags små benzinmotorer til plæneklippere, jordfræsere og andre små maskiner af denne type. Et af deres modelnavne er "Quantum".

Fordi usikkerhedsprincippet fortæller os, at visse målinger på atomniveau ikke kan foretages uden at forstyrre andre målinger, bruger nogle personer denne idé til at beskrive tilfælde i den menneskelige verden, hvor en observatørs aktivitet ændrer det, der observeres. En antropolog kan tage til et fjernt sted for at lære, hvordan folk lever der, men det faktum, at en fremmed person fra omverdenen er der og betragter dem, kan ændre den måde, som disse mennesker handler på.

Ting, som folk gør, mens de observerer ting, og som ændrer det, der observeres, er tilfælde af observatør-effekten. Nogle ting, som mennesker gør, forårsager ændringer på det meget lille niveau af atomer og er tilfælde af usikkerhed eller ubestemthed, som først beskrevet af Heisenberg. Usikkerhedsprincippet viser, at der altid er en grænse for, hvor småt vi kan foretage visse målepar som f.eks. position og hastighed eller bane og impuls. Observatørvirkningen siger, at det, som folk gør, når de observerer ting, f.eks. at lære om en myrekoloni ved at grave den op med haveredskaber, nogle gange kan have store virkninger, der ændrer det, som de forsøgte at lære noget om.