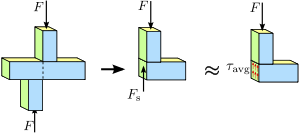Mekanisk spænding (stress) — definition, enheder (Pa) og beregning
Forstå mekanisk spænding: klar definition, SI-enheden pascal (Pa), formler og beregningstrin med praktiske eksempler til materialevalg og konstruktionsanalyse.
Spænding er den kraft pr. arealenhed på et legeme, der har tendens til at få det til at ændre form. Spænding beskriver altså hvordan eksterne kræfter overføres og fordeles inde i et materiale og er afgørende for at forudsige deformation og brud.
Stress er et mål for de interne kræfter i et legeme mellem dets partikler. Disse indre kræfter er en reaktion på de ydre kræfter, der påføres kroppen, og som får den til at skille sig ad, komprimere eller glide. De ydre kræfter er enten overfladekræfter eller kropskræfter. Stress er den gennemsnitlige kraft pr. arealenhed, som en partikel i et legeme udøver på en tilstødende partikel på tværs af en imaginær overflade, der adskiller dem. I kontinuumsmekanik antages det deformable legeme at være et kontinuum, så disse indre kræfter fordeles kontinuerligt i hele legemets volumen.
Typer af spænding
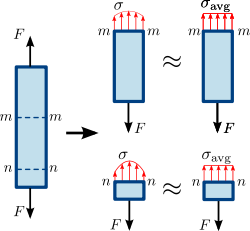
- Normalspænding (σ): virker vinkelret på en given flade og kan være træk (positiv) eller tryk (negativ). For en simpel enaksial belastning er formlen σ = F/A.
- Skærspænding (τ): virker parallel med en flade og forsøger at få materialets lag til at glide i forhold til hinanden. For en ensartet skæreflade kan man også skrive τ = F/A.
- Hydrostatisk (volumetrisk) spænding: lige store normalspændinger i alle retninger (f.eks. under et væsketryk).
- Principalspændinger: de tre normalspændinger i et koordinatsystem uden skærspændinger — nyttige til at bestemme hvor materiale mest sandsynligt vil svigte.
Matematisk beskrivelse
For en simpel enaksial normalspænding gælder:
σ = F A {\displaystyle {\sigma }={\frac {F}{A}}}}
hvor σ er spændingen, F er kraften og A er overfladearealet. For skærspænding bruger man ofte τ = F/A.
I fuld generalitet beskrives spænding i tredimensionelle materialer ved spændingstensoren σij (ofte kaldet Cauchy-spændingstensoren). I matrixform:
σ = [ [σ_xx, τ_xy, τ_xz], [τ_yx, σ_yy, τ_yz], [τ_zx, τ_zy, σ_zz] ]
Trajektorien (trækvektoren) på en flade med normals vektor n er givet ved t(n) = σ · n, hvor produktet er tensor-vektor multiplikation.
Enheder og konvertering
I SI-enheder måles kraften i newton og arealet i kvadratmeter. Det betyder, at spændingen er newton pr. kvadratmeter, eller N/m2. Spænding har imidlertid sin egen SI-enhed, kaldet pascal. 1 pascal (symbol Pa) er lig med 1 N/m2.
I britiske enheder måles spændingen i pund-kraft pr. kvadrattomme, som ofte forkortes til "psi". En typisk konvertering er:
- 1 Pa = 1 N/m2
- 1 MPa = 10^6 Pa
- 1 psi ≈ 6 894,76 Pa
Spændingsdimensionen er den samme som trykdimensionen, men betydningen fysisk er forskellig (tryk virker altid komprimerende, spænding kan være både træk og tryk).
Praktisk beregning — eksempel
Eksempel: En stang udsættes for en aksial trækkraft F = 1000 N, og tværsnitsarealet er A = 10 mm2 = 10·10^-6 m2. Spændingen bliver
σ = F / A = 1000 N / (10·10^-6 m2) = 1·10^8 Pa = 100 MPa.
Måling, fordeling og koncentrationer
Spændinger måles i praksis med metoder som strainsensorer (strain gauges), tensometri, akustiske emissionsteknikker og fotoelasticitet. Fordelingen af spænding i et komponent afhænger stærkt af geometri, belastningsretning, støttebetingelser og materialets egenskaber.
Lokale geometriændringer som hakk, huller, skarpe hjørner eller pludselige tværsnitsændringer skaber ofte spændingskoncentrationer, hvor den lokale spænding kan være mange gange højere end den gennemsnitlige spænding. Derfor er kroppens geometri ofte afgørende for, hvordan spændinger fordeles, og hvordan energi opbygges under påføring af den ydre kraft.
Materialeopførsel og svigt
Deformeringen som følge af spænding beskrives ofte ved deformation og tøjningsfelter. For lineært elastiske materialer gælder Hookes lov, der forbinder spænding og tøjning via materialets elasticitetsmoduler (f.eks. Youngs modulus). Hvis spændingen overstiger materialets flydegrænse eller brudstyrke, kan der opstå permanent deformation eller strukturelt svigt.
Til vurdering af styrke anvendes kriterier som f.eks. von Mises eller Tresca for at forudsige plastisk flytning i duktilt materiale, samt sammenligning med materialets nominelle styrke (yield strength, ultimate tensile strength). Ingeniører bruger ofte en sikkerhedsfaktor (safety factor) i dimensioneringen.
Modeller og antagelser
Nogle modeller i kontinuummekanik antager en gennemsnitlig kraft og kan overse geometriske faktorer. Mere avancerede modeller behandler kraft- og tøjningsfelter som rum- og tidsafhængige funktioner (felter), og benytter den fulde tensorielle beskrivelse for at få præcise resultater. Valget af model (lineær vs. ikke-lineær, statisk vs. dynamisk, elastisk vs. plastisk) påvirker de beregnede spændingsfordelinger og dermed vurderingen af sikkerhed og levetid.
Opsummering
- Spænding er intern kraft pr. areal (σ = F/A) og måles i pascal (Pa).
- Der findes normalspænding (vinkelret) og skærspænding (parallel), samt fuld tensoriel beskrivelse i 3D.
- Enhedskonverteringer og forståelse af geometriske effekter er vigtige i praksis — især pga. spændingskoncentrationer.
- For at vurdere risiko for svigt kombineres spændingsanalyse med materialdata (flydegrænse, brudstyrke) og relevante svigtkriterier.
Figur 1.4 Skubspænding i en prismatisk stang. Spændings- eller kraftfordelingen i stavens tværsnit er ikke nødvendigvis ensartet. Ikke desto mindre er en gennemsnitlig forskydningsspænding τ a v g {\displaystyle \tau _{\mathrm {avg} }\,\! }
Figur 1.3 Normalspænding i en prismatisk stang (et lige element med ensartet tværsnitsareal). Spændings- eller kraftfordelingen i stavens tværsnit er ikke nødvendigvis ensartet. En gennemsnitlig normalspænding σ a v g {\displaystyle \sigma _{\mathrm {avg} }\,\! }
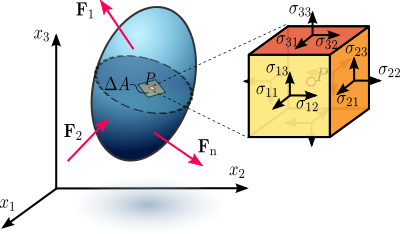
Figur 1.1 Spændinger i et belastet deformerbart materiale, der antages at være et kontinuum.
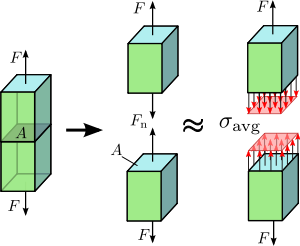
Figur 1.2 Axialspænding i en prismatisk stang, der er aksialt belastet.
Skubspænding
Yderligere oplysninger: Skubspænding
Simple spændinger
I nogle situationer kan spændingen i et objekt beskrives med et enkelt tal eller en enkelt vektor (et tal og en retning). Tre sådanne simple spændinger er den ensidige normalspænding, den simple forskydningsspænding og den isotrope normalspænding.
enaksial normalspænding
Trækspænding (eller spænding) er den spændingstilstand, der fører til udvidelse; det vil sige, at længden af et materiale har tendens til at stige i trækretningen. Materialets volumen forbliver konstant. Når der påføres lige store og modsatrettede kræfter på et legeme, kaldes den spænding, der skyldes denne kraft, for trækspænding.
I et ensidigt materiale øges længden derfor i trækspændingsretningen, mens de to andre retninger vil blive mindre i størrelse. I den uniaxiale spændingsmåde induceres trækspændingen af trækkræfter. Trækspænding er det modsatte af trykspænding.
Konstruktionselementer i direkte spænding er reb, jordankre og søm, bolte osv. Bjælker, der er udsat for bøjningsmomenter, kan indeholde trækspænding samt trykspænding og/eller forskydningsspænding.
Trækspændingen kan øges, indtil trækstyrken, dvs. grænsetilstanden for spændingen, er nået.
Spænding i endimensionale legemer
Alle virkelige genstande befinder sig i et tredimensionalt rum. Men hvis to dimensioner er meget store eller meget små i forhold til de andre, kan objektet modelleres som endimensionalt. Dette forenkler den matematiske modellering af objektet. En-dimensionelle objekter omfatter et stykke tråd, der er belastet i enderne og set fra siden, og en metalplade, der er belastet på forsiden og set tæt på og gennem tværsnittet.
Relaterede sider
- Spænding
- Bøjning
Spørgsmål og svar
Spørgsmål: Hvad er stress?
A: Stress er den kraft pr. arealenhed på et legeme, der har tendens til at få det til at ændre form. Det er et mål for de interne kræfter i et legeme mellem dets partikler og er den gennemsnitlige kraft pr. arealenhed, som en partikel i et legeme udøver på en tilstødende partikel på tværs af en imaginær overflade, der adskiller dem.
Sp: Hvordan påvirker ydre kræfter spændingen?
A: Eksterne kræfter er enten overfladekræfter eller kropskræfter, og de forårsager deformation af kroppens form, hvilket kan føre til permanent formændring eller strukturelt svigt, hvis materialet ikke er stærkt nok.
Spørgsmål: Hvad er formlen for enaksisk normalspænding?
A: Formlen for enakset normalspænding er σ = F/A, hvor σ er spændingen, F er kraften og A er overfladearealet. I SI-enheder måles kraften i newton og arealet i kvadratmeter, hvilket betyder, at spændingen er newton pr. kvadratmeter (N/m2). Der findes imidlertid en egen SI-enhed for spænding, kaldet pascal (Pa), som er lig med 1 N/m2. I britiske enheder ville den blive målt i pund-kraft pr. kvadrattomme (psi).
Sp: Hvad antager kontinuumsmekanikken om kraft?
Svar: Klassiske modeller for kontinuummekanik antager en gennemsnitlig kraft og tager ikke behørigt højde for geometriske faktorer - dvs. de tager ikke hensyn til, hvordan geometrien påvirker den måde, hvorpå energien opbygges under påføring af en ydre kraft.
Spørgsmål: Hvordan kan forskellige modeller give forskellige resultater, når man ser på deformation af stof og faste legemer?
A: Forskellige modeller ser forskelligt på deformation af stof og faste legemer, fordi stofs og faste legemers egenskaber er tredimensionelle - så hver tilgang tager hensyn til forskellige aspekter, hvilket kan føre til forskellige resultater.
Spørgsmål: Hvordan behandler kontinuumsmekanikken belastede deformerbare legemer?
A: Kontinuumsmekanikken behandler belastede deformerbare legemer som kontinua - hvilket betyder, at de indre kræfter fordeles kontinuerligt inden for volumenet af det materielle legeme i stedet for at være koncentreret på bestemte punkter, som det er tilfældet med klassiske modeller.
Søge