Drejningsmoment (kraftmoment): Definition, formel og eksempler
Lær drejningsmomentets definition, formel og praktiske eksempler — forstå momentarm, SI-enhed (Nm) og beregninger for simple maskiner og rotationssystemer.
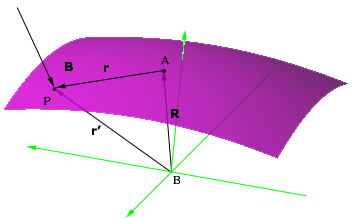
I fysik er kraftmomentet (ofte blot moment eller drejningsmoment) et mål for en krafts tendens til at få et legeme til at rotere om et bestemt punkt eller en bestemt akse. Momentet afhænger både af størrelsen af kraften og af hvor langt fra rotationsaksen kraften virker (momentarmen).
Momentarm og mekanisk fordel
Momentarmen er den vinkelrette afstand fra rotationsaksen til kraftens linje. En større momentarm giver større drejningsvirkning for samme kraft. Mange simple maskiner udnytter dette til at skabe mekanisk fordel, f.eks.:
- Håndtag (et langt håndtag øger momentet)
- Remskiver og tandhjul (ændrer effektive afstande og dermed moment)
- Nøddeknækkere, dåseåbnere og kobenstænger (typiske anvendelser af løftestangsprincippet)
SI-enhed
SI-enheden for moment er newtonmeter (N·m). Dimensionalt svarer det til kg·m²/s², men man bør ikke forveksle N·m med energi/bøjle J (joule), selvom en joule også kan udtrykkes som N·m — de beskriver forskellige fysiske størrelser.
Formel for moment
For et punkt hvor en kraft F virker i en afstand r fra rotationsaksen, gælder i to dimensioner for størrelsen (magnitude) af momentet:
Moment = Kraft × vinkelret afstand
I vektornotation (i 3D) beskrives momentet som krydsproduktet mellem positionsvektoren r og kraftvektoren F:
τ = r × F
Her peger τ (tau) vinkelret på det plan, som r og F spænder op, og retningen bestemmes af højrehåndsreglen.
Ligevægt og momentprincip
Hvis et legeme er i statisk ligevægt omkring en akse, gælder:
- Summen af alle drejningsmomenter (algebraisk) er nul.
- Med en simpel klokke/antiklokke-konvention: summen af de KLOKKESTILLEDE MOMENTER = summen af de ANTIKLOKKESTILLEDE MOMENTER.
Det bruges typisk ved beregning af kræfter i løftestænger og ved statikopgaver.
Eksempler
- En kraft på 10 N virker vinkelret på en arm med længde 0,5 m. Momentet er M = 10 N × 0,5 m = 5 N·m.
- Seesaw/udvekslingsproblem: En person på 100 N sidder 2,0 m fra støttepunktet. For at opnå ligevægt skal en modkraft F på 1,0 m-siden opfylde F × 1,0 m = 100 N × 2,0 m → F = 200 / 1 = 200 N.
- Løftestang: Hvis en belastning på 100 N ligger 0,2 m fra støttepunktet, og anstrengelsen virker 0,5 m fra støttepunktet, er den nødvendige anstrengelse: F = (100 N × 0,2 m) / 0,5 m = 40 N.
- Dørs hovedhåndtag: Et håndtag på 0,9 m og en skubbekraft på 5 N giver moment 5 × 0,9 = 4,5 N·m, hvilket bestemmer hvor let døren åbner.
Retning og højrehåndsregel
Momentets retning angives ved højrehåndsreglen: peger tommelfingeren i retning af τ, vil fingrene vise rotationens retning. I 2D-problemer bruger man ofte blot fortegnet (positiv/negativ) for at angive om rotationen er med- eller mod uret.
Relationer og anvendelser
- Effekt (power): Når et drejningsmoment τ får et legeme til at rotere med vinkelhastighed ω, er den mekaniske effekt P = τ · ω.
- Værktøj: Momentnøgle (torque wrench) bruges til at måle eller anvende et bestemt moment i fx bolteforbindelser.
- Skelnen: Moment af en kraft (drejningsmoment) er ikke det samme som momenter af massefordeling (fx inertimoment), selvom navnene ligner.
Afsluttende bemærkninger
Moment er et grundlæggende begreb i mekanik og ingeniørarbejde. Forståelse af kraftens størrelse, hvor den virker (momentarmen) og retningen (vektorielle egenskaber) er afgørende for at analysere rotation, stabile konstruktioner og design af mekaniske systemer.
En løftestang er et eksempel på en simpel maskine, hvor en kraft, der kaldes anstrengelsen, bruges til at overvinde en anden kraft, der kaldes belastningen. I fysik er et moment en kombination af en fysisk størrelse og en afstand.
Historien om øjeblikket
Momenterprincippet er afledt af Archimedes' opdagelse af løftestangens funktionsprincip. I løftestangen anvender man en kraft, på hans tid oftest en menneskelig muskel, på en arm, en bjælke af en slags. Archimedes bemærkede, at den kraft, der påføres genstanden, kraftmomentet, er defineret som M = rF, hvor F er den påførte kraft, og r er afstanden fra den påførte kraft til genstanden.
Spørgsmål og svar
Spørgsmål: Hvad er et styrkemoment?
Svar: Et kraftmoment, ofte blot benævnt moment, er et mål for tendensen til, at en kraft får en genstand til at rotere omkring et bestemt punkt eller en bestemt akse.
Sp: Hvilken rolle spiller momentarmen i dette begreb?
A: Momentarmen er afstanden fra rotationsaksen og spiller en vigtig rolle i dette begreb. Enkle maskiner som f.eks. håndtag, remskiver og tandhjul skaber mekanisk fordel ved at ændre momentarmen.
Spørgsmål: Hvad er SI-enheden for momenter?
A: SI-enheden for momenter er newtonmeter (kgm²/s²).
Spørgsmål: Hvad er formlen til beregning af momenter?
A: Formlen til beregning af momenter er: Moment = kraft × vinkelret afstand.
Sp: Hvilket princip gælder, når man overvejer momenter?
A: Momentprincippet siger, at når et system er i ligevægt, skal summen af dets momenter med uret være lig med summen af dets momenter mod uret.
Spørgsmål: Hvor er der eksempler på, hvor momenter anvendes?
A: Eksempler på momenter (drejeeffekt) omfatter løftestænger som f.eks. vipper, åbne og lukke døre, nøddeknækkere, dåseåbnere og kobenstænger.
Spørgsmål: Hvordan virker løftestænger med hensyn til kræfter og afstande?
A: En løftestang fungerer ved at bruge en kraft, der kaldes anstrengelse, til at overvinde en anden kraft, der kaldes belastning. I fysik kombinerer et moment både fysisk størrelse og afstand sammen.
Søge
