Gumbel-fordelingen: Definition og anvendelser i statistik for ekstreme værdier
Gumbel-fordelingen — forstå definition og anvendelser i statistik for ekstreme værdier til risikovurdering og forudsigelse af oversvømmelser, jordskælv og andre ekstreme hændelser.
Gumbel-fordelingen er en sandsynlighedsfordeling af ekstreme værdier.
I sandsynlighedsregning og statistik anvendes Gumbel-fordelingen til at modellere fordelingen af maksimum (eller minimum) af et antal prøver af forskellige fordelinger.
En sådan fordeling kan bruges til at repræsentere fordelingen af det maksimale vandspejl i en flod i et bestemt år, hvis der findes en liste over maksimumsværdier for de seneste ti år. Den er også nyttig til at forudsige chancen for, at et ekstremt jordskælv, en oversvømmelse eller en anden naturkatastrofe vil indtræffe.
Definition og formler
Gumbel-fordelingen beskriver typisk fordelingen af blokmaksima (f.eks. årlige maksimumsværdier). Den har to parametre: location μ og scale β > 0. Når man sætter z = (x − μ) / β, er fordelingsfunktion (CDF) og tæthed (PDF):
- F(x) = exp(−e^{−z}) = exp(−e^{−(x−μ)/β})
- f(x) = (1/β) e^{−z} e^{−e^{−z}} = (1/β) exp(−(x−μ)/β − e^{−(x−μ)/β})
Gumbel for maksimum kaldes ofte Gumbel‑right (eller gumbel_r). For minimum spejles fordelingsfunktionen (gumbel_l).
Vigtige egenskaber
- Forventning: E[X] = μ + γ β, hvor γ ≈ 0,5772156649 er Euler–Mascheroni‑konstanten.
- Varians: Var(X) = (π^2 / 6) β^2.
- Median: x_{0.5} = μ − β ln(ln 2).
- Skævhed (skewness) og andre højere momenter er konstante (uafhængige af μ og β) — skævheden er ≈ 1,139547.
- Gumbel er en særlig case af Generalized Extreme Value (GEV)‑fordelingen med shape parameter ξ = 0.
Anvendelser
Gumbel-fordelingen anvendes bredt i situationer, hvor man interesserer sig for ekstreme hændelser:
- Hydrologi: årlige maksimumsvandstande, flodtoppe og design af diger.
- Meteorologi: maksimum vindhastigheder, ekstreme nedbørshændelser.
- Ingeniørvidenskab: last‑ og styrkeberegninger ved ekstreme belastninger.
- Geofysik: sandsynlighed for store jordskælv eller tsunamier.
- Forsikring og finans: modellering af ekstreme tab eller risikobegivenheder.
Return‑niveauer (designværdier)
Et hyppigt anvendt begreb er T‑års return‑niveauet x_T, det niveau som forventes overskredet med sandsynlighed 1/T i et givet år. For Gumbel er kvantilen ved sandsynlighed p givet ved
x_p = μ − β ln(−ln p).
Hvis p = 1 − 1/T, fås T‑års return‑niveau:
x_T = μ − β ln(−ln(1 − 1/T)).
Eksempel: Hvis μ = 10 og β = 2, er 100‑års return‑niveau cirka x_100 ≈ 10 − 2·ln(−ln 0.99) ≈ 19.2.
Estimation og modelvalg
- MLE (Maximum Likelihood) anvendes ofte til at estimere μ og β numerisk.
- Metode af momenter kan bruges som en simpel tilgang; L‑momenter er populære i hydrologi, fordi de er robuste over for ekstreme værdier.
- Ved lille datamængde eller afhængighed i data (f.eks. serieafhængighed) bør man være forsigtig: blok‑maksima‑metoden kræver typisk uafhængighed og stationaritet.
- Modelvalidering: QQ‑plots, PP‑plots, Kolmogorov–Smirnov, Anderson–Darling og likelihood‑baserede tests bruges til at kontrollere tilpasning.
Begrænsninger og antagelser
- Gumbel antager, at blokmaksima konvergerer mod en GEV med ξ = 0. Hvis data er tungere halet, kan Fréchet (ξ > 0) være mere passende, og for lettere haler vælges Weibull (ξ < 0).
- Blok‑maksima‑metoden bruger kun maksimumsværdier fra hver blok (fx år), så meget information går tabt sammenlignet med peaks‑over‑threshold (POT) metoder, der bruger Generalized Pareto Distribution.
- Antagelser om stationaritet (ingen trend) og uafhængighed mellem blokke skal vurderes; ved klimatiske trends skal man inkludere tidsafhængige parametre eller anvende ikke‑stationære modeller.
Praktisk brug og software
- R: pakker som evd, ismev, extRemes og fitdistrplus tilbyder funktioner til tilpasning og diagnosticering.
- Python: scipy.stats.gumbel_r og scipy.stats.gumbel_l kan bruges til tæthed, fordelingsfunktion og simulering; avancerede ekstrem‑pakker findes også i eksterne biblioteker.
Opsummering
Gumbel‑fordelingen er et praktisk og ofte anvendt værktøj i ekstremværdestatistik til at beskrive fordelingen af blokmaksima. Den er let at anvende, har velkendte analytiske egenskaber og giver en enkel måde at beregne return‑niveauer på. Samtidig er det vigtigt at kontrollere antagelserne og overveje alternative ekstremmodeller, når data viser tungere eller lettere haler end Gumbel‑case'en.
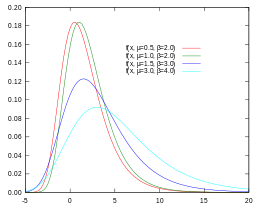
Gumbel-sandsynlighedsfordelingsfunktion (PDF)
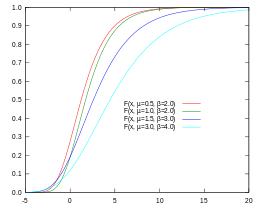
Gumbel kumulativ fordelingsfunktion (CDF)
Egenskaber
Gumbel-fordelingen er en kontinuert sandsynlighedsfordeling. Gumbel-fordelinger er en familie af fordelinger af samme generelle form. Disse fordelinger adskiller sig fra hinanden ved deres parametre for placering og skala: fordelingens gennemsnit ("gennemsnit") definerer dens placering, og standardafvigelsen ("variabilitet") definerer skalaen.
Man genkender Gumbel-sandsynlighedsdensitetsfunktionen (PDF) og Gumbel-kumulativ fordelingsfunktion (CDF).
I PDF-analysen findes sandsynligheden P for, at en værdi V forekommer mellem grænserne A og B, kort fortalt P(A<V<B), ved at beregne arealet under PDF-kurven mellem A og B.
| Eksempel på sandsynlighed i PDF-dokumentet |
| I figuren med den normale sandsynlighedsdensitetsfunktion skal værdierne på den vandrette akse være henholdsvis μ-3σ, μ-2σ, μ-1σ, μ+1σ, μ+2σ og μ+3σ. μ = middelværdi, σ = standardafvigelse. |
I modsætning til normalfordelingen er Gumbels PDF-format a-symmetrisk og skævt til højre.
CDF
I CDF'en findes sandsynligheden for, at en værdi V er mindre end A, direkte som CDF-værdien ved A:
P ( V ≤ A ) = C D F ( A ) {\displaystyle P(V\leq A)=CDF(A)}
| Eksempel på sandsynlighed i CDF'en |
| I Gumbel CDF-figuren angiver den røde kurve, at sandsynligheden for at V er mindre end 5 er 0,9 (eller 90 %), mens sandsynligheden for den mørkeblå linje er 0,7 eller 70 %. |

Den normale sandsynlighedstæthedsfunktion (PDF) er symmetrisk.
Matematik
CDF
Det matematiske udtryk for CDF'en er:
C D F ( A ) = e - e - e - ( A - μ ) / β , {\displaystyle CDF(A)=e^{-e^{-(A-\mu )/\beta }},}
hvor μ er modus (den værdi, hvor sandsynlighedstæthedsfunktionen når sit højdepunkt), e er en matematisk konstant, ca. 2,718, og β er en værdi relateret til standardafvigelsen (σ) :
β = σ 6 / π , {\displaystyle \beta =\sigma {\sqrt {6}}}/\pi ,}
hvor π er det græske symbol for Pi, hvis værdi er tæt på 22/7 eller 3,142, og symbolet {\displaystyle {\sqrt {\,\,}}}
Mode og median
Mode μ kan findes ud fra medianen M, som er den værdi af A, hvor CDF(A)=0,5, og β:
μ = M + β ln ( ln 2 ) , {\displaystyle \mu =M+\beta \ln \ln \ venstre(\ln 2\ højre),}
hvor ln er den naturlige logaritme.
Gennemsnitlig
Middelværdien, E(x), er givet ved:
E ( x ) = μ + c β , {\displaystyle \operatornavn {E} (x)=\mu +c\beta ,}
hvor c {\displaystyle c}

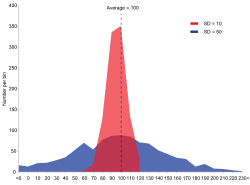
Der er to dataserier: rød og blå. Begge har samme middelværdi (gennemsnit) : 100, men den blå gruppe har en større standardafvigelse (SD=σ=50) end den røde gruppe (SD=σ=10).
Vurdering
I en dataserie kan parametrene mode (μ) og β estimeres ud fra gennemsnittet, medianen og standardafvigelsen. Beregningen af de tre sidstnævnte størrelser forklares på de respektive Wiki-sider. Derefter kan faktorerne μ og β beregnes ved hjælp af formler, der er angivet i det foregående afsnit. På denne måde kan CDF'en for den Gumbel-fordeling, der hører til dataene, bestemmes, og sandsynligheden for interessante dataværdier kan findes.

Tilpasset kumulativ Gumbel-fordeling til de maksimale regnmængder i oktober på en dag ved hjælp af CumFreq
Ansøgning
Inden for hydrologi anvendes Gumbel-fordelingen til at analysere variabler som månedlige og årlige maksimumsværdier for daglige nedbørsmængder og flodudløbsmængder samt til at beskrive tørkeperioder.
Det blå billede illustrerer et eksempel på tilpasning af Gumbel-fordelingen til de rangordnede maksimale regnmængder for en dag i oktober, der også viser 90 % konfidensbæltet baseret på binomialfordelingen.
Spørgsmål og svar
Q: Hvad er Gumbel-fordelingen?
A: Gumbel-fordelingen er en sandsynlighedsfordeling af ekstreme værdier.
Q: Hvad bruges Gumbel-fordelingen til?
A: Gumbel-fordelingen bruges til at modellere fordelingen af maksimum (eller minimum) for et antal stikprøver af forskellige fordelinger.
Q: Hvordan kan Gumbel-fordelingen bruges til at forudsige naturkatastrofer?
A: Gumbel-fordelingen er nyttig til at forudsige chancen for, at et ekstremt jordskælv, en oversvømmelse eller en anden naturkatastrofe vil finde sted.
Q: Hvad er et eksempel på at bruge Gumbel-fordelingen til at repræsentere en tidligere begivenhed?
A: Gumbel-fordelingen kunne bruges til at repræsentere fordelingen af det maksimale niveau i en flod i et bestemt år, hvis der var en liste over de maksimale værdier for de sidste ti år.
Q: Er Gumbel-fordelingen kun nyttig til at forudsige naturkatastrofer?
A: Nej, Gumbel-fordelingen kan bruges til at modellere fordelingen af ekstreme værdier i enhver situation.
Q: Kan Gumbel-fordelingen bruges til at modellere minimumsværdien af et sæt stikprøver?
A: Ja, Gumbel-fordelingen kan bruges til at modellere fordelingen af enten maksimum eller minimum for et sæt stikprøver.
Q: Er Gumbel-fordelingen en almindeligt anvendt fordeling i sandsynlighedsteori og statistik?
A: Ja, Gumbel-fordelingen er en almindeligt anvendt fordeling i sandsynlighedsteori og statistik, især til modellering af ekstreme værdier.
Søge



