Sandsynlighedsrum
Sandsynlighedsrum er en matematisk model, der bruges til at beskrive videnskabelige eksperimenter Et sandsynlighedsrum består af tre dele:
- Et prøveområde, der indeholder alle mulige udfald
- En række begivenheder. Hver begivenhed har nul eller flere resultater.
- En funktion, der tildeler sandsynligheder til hver enkelt begivenhed
Et resultat er resultatet af en enkelt udførelse af modellen. Da individuelle resultater kan være af ringe praktisk værdi, anvendes mere komplekse begivenheder til at karakterisere grupper af resultater. Samlingen af alle sådanne hændelser er en σ-algebra F {\displaystyle \scriptstyle {\mathcal {F}}} 
. Endelig er der behov for at specificere hver enkelt hændelses sandsynlighed for at indtræffe. Dette gøres ved hjælp af sandsynlighedsmålsfunktionen P.
Når sandsynlighedsrummet er etableret, antages det, at "naturen" gør sit træk og vælger et enkelt resultat, ω, fra prøveområdet Ω. Alle begivenheder i F {\displaystyle \scriptstyle {\mathcal {F}}}}, der indeholder det valgte udfald ω (husk, at hver begivenhed er en delmængde af Ω), siges at "have fundet sted". Den udvælgelse, som naturen foretager, sker på en sådan måde, at hvis eksperimentet blev gentaget et uendeligt antal gange, ville de relative hyppigheder for forekomst af hver af begivenhederne falde sammen med de sandsynligheder, som er foreskrevet af funktionen P.
Den fremtrædende sovjetiske matematiker Andrey Kolmogorov introducerede begrebet sandsynlighedsrum sammen med andre sandsynlighedsaksiomer i 1930'erne.
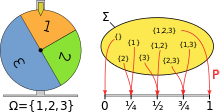
Modellering af et lykkehjul ved hjælp af sandsynlighedsrum
Spørgsmål og svar
Spørgsmål: Hvad er et sandsynlighedsrum?
A: Et sandsynlighedsrum er en matematisk model, der bruges til at beskrive videnskabelige eksperimenter. Den består af tre dele: et prøveområde, som opregner alle mulige udfald, et sæt af begivenheder, som associerer nul eller flere udfald, og en funktion, som tildeler sandsynligheder til hver enkelt begivenhed.
Sp: Hvad består prøveområdet af?
Svar: Prøveområdet består af alle mulige udfald, ofte skrevet som Ω {\displaystyle \Omega } , og et udfald som ω {\displaystyle \omega } .
Spørgsmål: Hvad er et udfald?
Svar: Et resultat er resultatet af en enkelt udførelse af modellen.
Sp: Hvad bruges begivenheder til i sandsynlighedsrum?
Svar: Begivenheder anvendes til at karakterisere grupper af resultater, da individuelle resultater måske ikke er til megen praktisk nytte. Samlingen af alle sådanne hændelser kaldes en σ-algebra, der undertiden skrives som F {\displaystyle {\mathcal {F}}} .
Spørgsmål: Hvordan tildeles sandsynligheder til hver enkelt hændelse?
Svar: Sandsynlighederne tildeles hver enkelt begivenhed ved hjælp af sandsynlighedsmålfunktionen P.
Spørgsmål: Hvem har indført begrebet sandsynlighedsrum? Svar: Den fremtrædende sovjetiske matematiker Andrey Kolmogorov introducerede begrebet sandsynlighedsrum sammen med andre sandsynlighedsaksiomer i 1930'erne.
