Parallelt postulat
I geometri er parallelitetspostulatet et af aksiomerne i euklidisk geometri. Nogle gange kaldes det også Euklids femte postulat, fordi det er det femte postulat i Euklids Elementer.
Postulatet siger, at:
Hvis du skærer et linjestykke med to linjer, og de to indvendige vinkler, som linjerne danner, er mindre end 180°, så vil de to linjer til sidst mødes, hvis du forlænger dem længe nok.
Det geometriske område, som følger alle Euklids aksiomer, kaldes euklidisk geometri. Geometrier, som ikke følger alle Euklids aksiomer, kaldes ikke-euklidisk geometri.
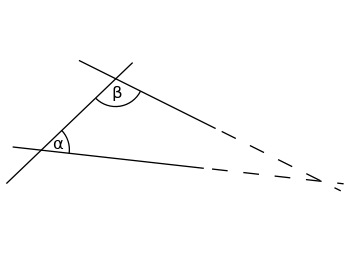
Hvis summen af de indre vinkler α (alpha) og β (beta) er mindre end 180°, vil de to linjer skære hinanden et sted, hvis de begge forlænges til uendelig.
Historie
Nogle matematikere mente, at Euklids femte postulat var meget længere og mere kompliceret end de fire andre postulater. Mange af dem mente, at det kunne bevises ud fra de andre enklere aksiomer. Nogle matematikere meddelte, at de havde bevist sætningen ud fra de enklere sætninger, men det viste sig, at de alle tog fejl.
Playfairs aksiom
En anden nyere sætning, kendt som Playfairs aksiom, svarer til Euklids femte postulat. Det siger, at:
Hvis du har en ret linje og et punkt, der ikke ligger på denne linje, kan du kun tegne én ret linje gennem dette punkt, som ikke møder den anden ret linje.
Faktisk fandt matematikerne ud af, at dette aksiom ikke blot ligner Euklids femte postulat, men at det har præcis de samme implikationer. Matematisk set kaldes de to sætninger for "ækvivalente" sætninger. I dag anvendes Playfairs aksiom oftere af matematikere end Euklids oprindelige parallelle postulat.
Ikke-euklidisk geometri
Til sidst forsøgte nogle matematikere at bygge nye geometrier uden at bruge aksiometrierne. En form for ikke-euklidisk geometri kaldes elliptisk geometri. I elliptisk geometri er parallelpostulatet erstattet af et aksiom, der siger, at:
Hvis man har en ret linje og et punkt, der ikke ligger på denne linje, kan man ikke tegne en ret linje gennem dette punkt, som ikke til sidst vil krydse den anden ret linje.
Matematikere fandt ud af, at når de erstattede Euklids femte postulat med dette aksiom, var de stadig i stand til at bevise mange af Euklids andre teoremer. En måde at forestille sig elliptisk geometri på er ved at tænke på overfladen af en klode. På en globus ser længdegraderne ud til at være parallelle ved ækvator, men de mødes alle ved polerne. Sidst i det 19. århundrede blev det vist, at den elliptiske geometri er konsistent. Dette beviste, at Euklids femte postulat ikke var uafhængigt af de andre postulater. Herefter holdt matematikerne for det meste op med at forsøge at bevise det femte postulat ud fra de fire andre postulater. I stedet begyndte mange matematikere at studere andre geometrier, som ikke følger Euklids femte postulat.
Et andet aksiom, som matematikere nogle gange erstatter Euklids femte aksiom med, siger, at:
Hvis du har en ret linje og et punkt, der ikke ligger på denne linje, kan du tegne mindst to rette linjer gennem dette punkt, som ikke krydser den anden rette linje.
Dette kaldes hyperbolisk geometri.
En anden geometri fjerner blot Euklids femte postulat og erstatter det ikke med noget som helst. Dette kaldes neutral geometri eller absolut geometri.
Søge