Tyngdeacceleration (g): Definition, standardværdi og variationer
Få klar definition af tyngdeacceleration (g), standardværdien 9,80665 m/s², målemetoder og hvordan g varierer lokalt på Jordens overflade.
Den acceleration, som et objekt opnår på grund af tyngdekraften, kaldes tyngdeacceleration. Dens SI-enhed er m/s2. Tyngdeacceleration er en vektor, hvilket betyder, at den både har en størrelse og en retning; ved Jordens overflade peger den i hovedsagen mod Jordens centrum. Tyngdeaccelerationen ved jordens overflade repræsenteres sædvanligvis med bogstavet g. Den internationale standardværdi (konventionel reference) er 9,80665 m/s2 (32,1740 ft/s2), men den faktiske acceleration for et legeme i frit fald varierer med sted og højde.
Hvorfor varierer g?
Der er flere årsager til, at g ikke er helt ens overalt:
- Rotation af Jorden: Centrifugalkraften ved Jordens rotation reducerer den effektive tyngde mest ved ækvator og mindst ved polerne.
- Jordens form: Jorden er ikke en perfekt kugle men en fladtrykt sfæroid (oblat), hvilket betyder, at afstand fra overfladen til Jordens centrum er større ved ækvator end ved polerne — det nedsætter g ved ækvator.
- Højde: Jo længere væk fra Jordens massecentrum (større højde), desto mindre bliver tyngdekraften efter Newtons lov (omtrent aftagende med afstanden i anden potens).
- Lokale massevariationer: Forskelle i bjergmasse, geologiske strukturer og tæthed i undergrunden giver små lokale afvigelser i g.
Typiske værdier og størrelsesorden
- Standardværdien ved havoverfladen: 9,80665 m/s2.
- Ved ækvator: cirka 9,780 m/s2.
- Ved polerne: cirka 9,832 m/s2.
- Ændring med højde: g aftager med højden; omtrentlig reduktion er omkring 3,1·10-6 m/s2 pr. meter (dvs. ~0,0031 m/s2 pr. km) tæt på Jordens overflade.
- Lokale variationer måles ofte i mGal (1 mGal = 10-5 m/s2) eller mikroGal; geofysiske anomalier kan typisk være fra nogle få mGal til nogle hundrede mGal afhængigt af regionen.
Enkle formler (til orientering)
For små højder h over Jordens overflade kan man approximere ændringen i g med
g(h) ≈ g0 · (R / (R + h))2,
hvor R er Jordens radius og g0 tyngdeaccelerationen ved overfladen. Til første orden giver dette den nævnte nedgang på ~3,1·10-6 m/s2 per meter.
Målemetoder
Tyngdeacceleration måles med forskellige instrumenter:
- Fritfalds- eller absolutte gravimetre (laserinterferometri måler tiden for en frit faldende reflektor): meget præcise, bruges til referencemålinger.
- Superledende gravimetre: ekstremt følsomme for tidsvarende ændringer i g (tidevand, seismik).
- Pendelmetoder: historisk vigtig — periodetiden for en pendul afhænger af g.
- Atominterferometri: moderne, meget nøjagtige målinger ved hjælp af kvanteinterferens af kolde atomer.
Anvendelser
- Kalibrering af vægte og sensorer, præcisionsmålinger i laboratorier.
- Geofysik og geodesi: kortlægning af undergrundens tætheder og struktur ved at måle lokale tyngdefelter.
- Raket- og satellitbaner: nøjagtig viden om tyngdefeltet er nødvendig for baneplanlægning og navigation.
- Fysik: tests af fundamentale love (f.eks. Newtons gravitationslov) og præcise eksperimenter som måling af G eller søgning efter nye fysik-fænomener.
Skelnen mellem tyngdeacceleration og gravitationsacceleration
Ofte skelnes mellem den rene gravitationsacceleration (årsaget af masse) og den tilsyneladende tyngdeacceleration, som også inkluderer effekten af ikke-inertielle kræfter som centrifugalkraft fra Jordens rotation. Når man taler om "g" i hverdagen eller i mange tekniske sammenhænge, mener man normalt den effektive, målte værdi inkl. rotationsbidraget.
Samlet set er g en veldefineret standardværdi for reference, men den lokale og højdeafhængige variation betyder, at nøjagtige beregninger og målinger altid skal tage hensyn til position og de relevante korrektioner.
Hvorfor tungere genstande ikke falder hurtigere end lettere genstande
Isaac Newton fandt ud af, at den resulterende kraft er lig med masse gange acceleration, eller med symbolerne F = m a {\displaystyle F=ma}
. Dette kan omformuleres til a = F m {\displaystyle a={\frac {F}{m}}}\ } 
. Jo større masse den faldende genstand har, jo større er den tyngdekraft, der trækker den mod Jorden. I ligningen ovenfor er dette F {\displaystyle F}
. Imidlertid er det antal gange, hvor kraften bliver større eller mindre, lig med det antal gange, hvor massen bliver større eller mindre, idet forholdet forbliver konstant. I alle situationer ophæves F m {\displaystyle {\frac {\frac {F}{m}}}} }
ned til den ensartede acceleration på ca. 9,8 m/s2 . Det betyder, at alle frit faldende genstande uanset deres masse accelererer med samme hastighed.
Se følgende eksempler:
a = 49 N 5 k g = 9,8 N / k g = 9,8 m / s 2 {\displaystyle a={\frac {49\,\mathrm {N} }{5\,\mathrm {kg} }}\\ =9.8\,\mathrm {N/kg} =9.8\,\mathrm {m/s^{2}}} } 
a = 147 N 15 k g = 9,8 N / k g = 9,8 m / s 2 {\displaystyle a={\frac {147\,\mathrm {N} }{15\,\mathrm {kg} }}\\ =9.8\,\mathrm {N/kg} =9.8\,\mathrm {m/s^{2}}} } 
Overfladeacceleration
Afhængigt af stedet falder en genstand på Jordens overflade med en acceleration på mellem 9,76 og 9,83 m/s2 (32,0 og 32,3 ft/s2 ).
Jorden er ikke helt kugleformet. Den ligner en "sammenpresset" kugle, hvor radius ved ækvator er lidt større end radius ved polerne. Dette bevirker, at tyngdeaccelerationen øges en smule ved polerne (da vi er tæt på Jordens centrum, og tyngdekraften afhænger af afstanden) og mindskes en smule ved ækvator. På grund af centripetalaccelerationen er tyngdeaccelerationen også lidt mindre ved ækvator end ved polerne. Ændringer i tætheden af sten under jorden eller tilstedeværelsen af bjerge i nærheden kan påvirke tyngdeaccelerationen en smule.
Højde
Et objekts acceleration ændrer sig med højden. Ændringen i tyngdeaccelerationen med afstanden fra Jordens centrum følger en omvendt firkantet lov. Det betyder, at tyngdeaccelerationen er omvendt proportional med kvadratet på afstanden fra Jordens centrum. Når afstanden fordobles, falder gravitationsaccelerationen med en faktor 4. Når afstanden tredobles, falder gravitationsaccelerationen med en faktor 9 osv.
gravitationsacceleration ∝ 1 afstand 2 {\displaystyle {\mbox{gravitationsacceleration}}\ \propto \ {\frac {1}{{{\mbox{distance}}}^{2}}}}}}\ } 
gravitationsacceleration × afstand 2 = k {\displaystyle {\mbox{gravitationsacceleration}}\ gange {{{\mbox{afstand}}^{2}}}\ ={k}} 
Ved jordens overflade er tyngdeaccelerationen ca. 9,8 m/s2 (32 ft/s2 ). Den gennemsnitlige afstand til Jordens centrum er 6 371 km (3 959 mi).
k = 9,8 × 6371 2 {\displaystyle {k}={\mbox{9,8}}\\ gange {{\mbox{6371}}}^{2}}}} 
Ved hjælp af konstanten k {\displaystyle k} 
kan vi beregne tyngdeaccelerationen i en bestemt højde.
gravitationsacceleration = k afstand 2 {\displaystyle {\mbox{gravitationsacceleration}}}\ ={\frac {k}{{{{\mbox{distance}}}^{2}}}}}}} } 
Eksempel: Find tyngdeaccelerationen 1.000 km over Jordens overflade.
6371 + 1000 = 7371 {\displaystyle 6371+1000=7371} 
∴ Afstanden fra Jordens centrum er 7.371 km (4.580 mi).
gravitationsacceleration = 9,8 × 6371 2 7371 2 ≈ 7,3 {\displaystyle {\mbox{gravitationsacceleration}}}\ ={{\frac {{\mbox{9,8}}}\ \ gange {{{\mbox{6371}}}^{2}}}}{{{\mbox{7371}}}^{2}}}}\ \approx 7,3} 
∴ Acceleration som følge af tyngdekraften 1.000 km over Jordens overflade er 7,3 m/s2 (24 ft/s2 ).
Gravitationsaccelerationen ved Kármán-linjen, grænsen mellem Jordens atmosfære og det ydre rum, som ligger i 100 km højde, er kun ca. 3 % lavere end ved havniveau.
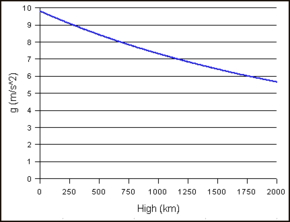
Ændring i tyngdeaccelerationen med højden af et objekt
Spørgsmål og svar
Q: Hvad er tyngdeacceleration?
A: Acceleration på grund af tyngdekraften er den acceleration, som et objekt opnår på grund af tyngdekraften.
Q: Hvad er SI-enheden for tyngdeacceleration?
A: SI-enheden for tyngdeacceleration er m/s2.
Q: Er tyngdeaccelerationen en skalar eller en vektor?
A: Tyngdeaccelerationen er en vektor, fordi den både har en størrelse og en retning.
Q: Hvad er det symbol, der bruges til at repræsentere tyngdeaccelerationen på jordens overflade?
A: Det symbol, der bruges til at repræsentere tyngdeaccelerationen på jordens overflade, er g.
Q: Hvad er standardværdien for tyngdeaccelerationen ved Jordens overflade?
A: Standardværdien for tyngdeaccelerationen ved Jordens overflade er 9,80665 m/s2 (32,1740 ft/s2).
Q: Varierer den faktiske acceleration af et legeme i frit fald med stedet?
A: Ja, den faktiske acceleration af et legeme i frit fald varierer med stedet.
Q: Hvad er definitionen på tyngdeacceleration?
A: Tyngdeacceleration er den acceleration, som et objekt opnår på grund af tyngdekraften, og den repræsenteres af bogstavet g med en standardværdi på 9,80665 m/s2 på jordens overflade, mens den faktiske acceleration kan variere med stedet.
Søge