Lysuret: Hvordan et lysur illustrerer tidsudvidelse i relativitetsteorien
Lysuret: Visuel forklaring på tidsudvidelse i relativitetsteorien — hvordan et lysur demonstrerer, at tid går langsommere for bevægende systemer.
Hvad er et lysur?
Lysuret er en enkel og tydelig illustration af et grundlæggende træk ved den specielle relativitetsteori på. Et lysur består af en lyskilde i bunden af en stang og et spejl i toppen: et kort lysglimt sendes op, reflekteres i spejlet og registreres i bunden, hvor det trigger næste blink. Hvert tilbagevendende blink registreres som et "tick". Fordi lysets hastighed er konstant for alle observatører, bruges et lysur ofte til at forklare, hvordan bevægelse påvirker måling af tid.
Inden vi går i detaljer, kan du forestille dig en enklere, ikke-relativistisk analog: en basketballspiller i lastrummet på et fly, der dribler. Passagerer i flyet ser boldens studsning foregå på stedet (i flyets ramme), mens observatører på jorden ser, at bolden samtidig bevæger sig langt i jordens ramme. På samme måde vil observatører på jorden og i et fly/værelsesystem måle forskellige afstande og tider for samme begivenhed, når systemerne bevæger sig i forhold til hinanden.
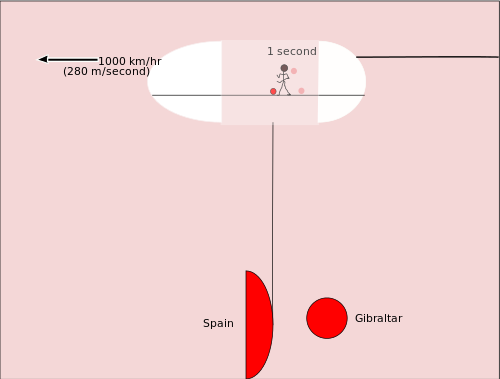
Lysuret i ro og i bevægelse
Antag først et lysur, der står stille i forhold til et observatorium (f.eks. ved Nordpolen). Hvis stangens længde fra bund til spejl er a, bevæger lyset sig en afstand 2a for ét helt tick (op og ned). Fordi afstand = hastighed × tid, og lysets hastighed er c, er tiden mellem to ticks for et ur i hvile
t = 2a / c
I eksemplet fra teksten tog man a = 0,5 km, så lyset bevæger sig 1 km per tick, og
t = 1 km / 300.000 km/s = 1/300.000 s ≈ 0,00000333... s
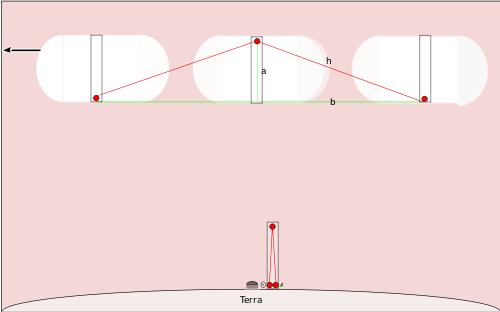
Hvad ser en observatør på Jorden, når uret bevæger sig?
Forestil dig nu, at et rumskib flyver over Nordpolen med hastighed r (rumskibets pol er parallel med stangen i tidligere eksempel), og at uret er identisk med det stationære ur (samme a). For observatører på Jorden bevæger spejlet sig horisontalt, mens lyset bevæger sig diagonalt op til spejlet og diagonalt ned igen. De enkelte strækninger (op og ned) er hypotenuser i en retvinklet trekant.
Hvis t' er den tid, som observatøren på Jorden måler mellem to ticks af det bevægende ur, så bevæger rumskibet sig en horisontal afstand r t'/2 i opad-øjeblikket (og igen i nedad-øjeblikket). Den diagonale afstand fra bund til spejl (halvvejen) bliver derfor
h = √( a2 + (r t'/2)2 )
Hele lysstrækningen i et tick (op + ned) er
d = 2 h = 2 √( a2 + (r t'/2)2 )
Da lyset altid bevæger sig med hastighed c, gælder også i jordens ramme
c t' = d = 2 √( a2 + (r t'/2)2 )
Udledning af tidsudvidelsen
Vi løser ligningen for t'. Først kvadrerer vi begge sider og forenkler:
(c t'/2)2 = a2 + (r t'/2)2
(c2 t'2)/4 − (r2 t'2)/4 = a2
t'2 (c2 − r2)/4 = a2
t'2 = 4 a2 / (c2 − r2) = (4 a2 / c2) · 1 / (1 − r2/c2)
Men 2a/c er netop tiden mellem ticks for uret i dets egen hvileramme (t), altså t = 2a / c. Indsætter vi dette får vi den velkendte form:
t' = t / √(1 − r2 / c2)
Dette viser, at et ur, der bevæger sig med hastighed r i forhold til en observatør, aflæses som langsommere af denne observatør. Faktorens 1 / √(1 − r2/c2) kaldes ofte den Lorentz-faktor (γ).
Eksempel
Hvis uret i hvile har t = 1 sekund mellem ticks, og rumskibet bevæger sig med r = 0,5 c, så er
t' = 1 / √(1 − 0,52) = 1 / √(1 − 0,25) = 1 / √0,75 ≈ 1,1547 sekunder.
Det bevægende ur ser altså ud til at "tikke" langsommere med en faktor ≈ 1,1547, set fra Jorden.
Hvad betyder det i praksis?
- Tidsudvidelse er ikke bare en teoretisk kuriosa: den er eksperimentelt verificeret — fx ved målinger af muoners levetid i atmosfæren og ved præcisionsure i rumfart (GPS-systemet korrigerer for relativistiske effekter).
- Begrebet afhænger af, hvilken ramme man betragter som reference. Den tid, der måles i et ur, der er i hvile i sin egen ramme (f.eks. en observatør med uret fastspændt), kaldes ofte egentid eller proper tid. Observatører i andre rammer måler en længere tid mellem de samme to hændelser (dvs. uret ses til at gå langsommere).
Du kan lege med forskellige hastigheder og se, hvordan tidsudvidelsen vokser, fx på: http://www.1728.org/reltivty.htm
Hvis du vil have en kort opsummering eller en trinvis udregning tilpasset andre talværdier (fx for r = 0,9c eller r tæt på c), så skriv gerne, hvilke værdier du vil prøve.
Spørgsmål og svar
Spørgsmål: Hvad er lysuret?
A: Lysuret er en anordning, der er designet til at demonstrere et grundlæggende træk ved den specielle relativitetsteori. Det fungerer ved at lade et lysglimt prelle af på et fjernt spejl og bruge dets tilbagevenden til at udløse et andet lysglimt, samtidig med at det tæller, hvor mange lysglimt der har været undervejs.
Spørgsmål: Hvad er tidsudvidelse?
Svar: Tidsudvidelse er en effekt, der opstår, når mennesker på Jorden ser et rumskib flyve hen over os med et lysur. De vil se, at det tikker relativt langsomt på grund af relativitetseffekten.
Spørgsmål: Hvordan kan vi beregne, hvor meget tiden bliver langsommere på rumskibet?
Svar: Vi kan bruge algebra og Pythagoras' sætning til at beregne, hvor meget tiden bliver langsommere på rumskibet. Vi skal anvende ligningen d = rt (afstand er lig med hastighed gange tid) og bruge den konstante lyshastighed c i to opgaver.
Spørgsmål: Hvordan fungerer lysuret?
A: Lysuret består af en lysudgang i bunden af en lang stang med et spejl i toppen og en elektronisk detektor i bunden. Når det startes, går et lysblinken fra bunden til toppen, hvor det reflekteres tilbage nedad igen, når det opfanges af detektoren i bunden, som lægger en tæller til den vedlagte tæller og affyrer endnu et blink opad igen. Denne proces fortsætter, indtil den stoppes eller nulstilles.
Spørgsmål: Hvilken ligning skal vi bruge til denne beregning?
A: Vi skal bruge t' = 2a/(c√(1-r2/c2)), som siger, at t' (tiden mellem ticks på uret på Nordpolen) er lig med 2a/c divideret med √(1-r2/c2). Hvor t = 1 sekund, hvis man rejser med halv lysets hastighed, så er t' = 1,1547 sek.
Sp: Hvad har Pythagoras' sætning med denne beregning at gøre?
Svar: Pythagoras' sætning hjælper os med at finde ud af h (hypotenusen), som indgår i vores ligning til beregning af, hvor lang tid hvert tick tager i sekunder (d=ct). Når vi kender h, kan vi løse t', som fortæller os, hvor lang tid hvert tick tager ifølge mennesker på Jorden, der ser det fra Nordpolen, og dem om bord på skibet selv, der rejser meget hurtigt over dem
Søge