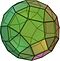
Archimedisk fast stof
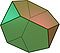
I geometri er et arkimedisk fast stof en konveks form, der består af polygoner. Det er et polyeder med følgende egenskaber:
- Hver flade består af en regelmæssig polygon
- Alle hjørnerne af formen ser ens ud
- Formen er hverken et platonisk fast stof, et prisme eller et antiprisme.
Afhængigt af hvordan man tæller dem, er der tretten eller femten af disse former. Af to af disse figurer findes der to versioner, som ikke kan gøres kongruente ved hjælp af rotation. De arkimediske faste legemer er opkaldt efter den antikke græske matematiker Archimedes, som sandsynligvis opdagede dem i det 3. århundrede f.Kr. Archimedes' skrifter er gået tabt, men Pappus af Alexandria opsummerede dem i det 4. århundrede. I renæssancen satte kunstnere og matematikere pris på rene former og genopdagede alle disse former. Johannes Kepler afsluttede sandsynligvis denne søgen omkring 1620.
Der skal mindst to forskellige polygoner til for at konstruere et arkiimedisk rum.
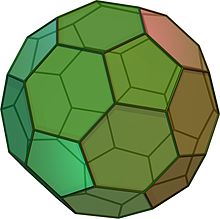
Et afkortet isosaeder ligner en fodbold. Den består af 12 ligesidede femkanter og 20 regelmæssige sekskanter. Det har 60 hjørner og 90 kanter. Det er et arkimedisk rum
Egenskaber
- Arkimediske faste legemer består af regelmæssige polygoner, og derfor har alle kanter samme længde.
- Alle arkimediske faste legemer kan fremstilles af platoniske faste legemer ved at "skære kanterne" af de platoniske faste legemer.
- Den type polygoner, der mødes i et hjørne ("toppunkt"), karakteriserer både det arkimediske og det platoniske faste stof
Forbindelse med platoniske faste legemer
Platoniske faste legemer kan omdannes til arkimediske faste legemer ved at følge en række regler for deres konstruktion.
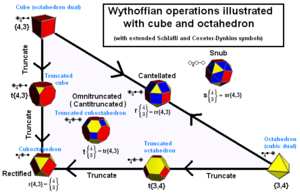
Archimedeans faste legemer kan konstrueres som generatorpositioner i et kalejdoskop
Oversigt over arkimediske faste legemer
Følgende er en liste over alle arkimediske faste legemer
| Billede | Navn | Ansigter | Type | Kanter | Toppene |
|
| Afkortet tetraeder | 8 | 4 trekanter 4 sekskanter | 18 | 12 |
|
| 14 | 8 trekanter 6 firkanter | 24 | 12 | |
|
| Afkortet terning | 14 | 8 trekanter 6 ottekanter | 36 | 24 |
|
| Afkortet oktaeder | 14 | 6 firkanter 8 sekskanter | 36 | 24 |
|
| Rhombikuboktaeder | 26 | 8 trekanter 18 firkanter | 48 | 24 |
|
| Afkortet kuboktaeder | 26 | 12 firkanter 8 sekskanter 6 ottekanter | 72 | 48 |
|
| Snub cube (2 spejlede versioner) | 38 | 32 trekanter 6 firkanter | 60 | 24 |
|
| Icosidodekaeder | 32 | 20 trekanter 12 femkanter | 60 | 30 |
|
| Afkortet dodekaeder | 32 | 20 trekanter 12 decagoner | 90 | 60 |
|
| Afkortet isosaeder | 32 | 12 femkanter 20 sekskanter | 90 | 60 |
|
| Rhombicosidodekaeder | 62 | 20 trekanter30 firkanter12 | 120 | 60 |
|
| Afkortet icosidodekaeder | 62 | 30 firkanter 20 sekskanter 12 decagoner | 180 | 120 |
|
| Snub dodekaeder (2 spejlede versioner) | 92 | 80 trekanter 12 femkanter | 150 | 60 |
Spørgsmål og svar
Spørgsmål: Hvad er et arkimedisk fast stof?
A: Et arkimedisk fast stof er en konveks form bestående af polygoner, som har de egenskaber, at hver side er en regulær polygon, at alle hjørner ser ens ud, og at det ikke er et platonisk fast stof, et prisme eller et antiprisme.
Sp: Hvor mange arkimediske faste legemer findes der?
Svar: Afhængigt af hvordan de tælles, er der enten tretten eller femten arkimediske faste legemer.
Spørgsmål: Hvem opdagede de arkimediske faste legemer?
A: De arkimediske faste størrelser er opkaldt efter den gamle græske matematiker Archimedes, som sandsynligvis opdagede dem i det 3. århundrede f.Kr.
Spørgsmål: Hvad gjorde Pappus af Alexandria med Archimedes' skrifter?
Svar: Pappus af Alexandria opsummerede Archimedes' skrifter om de arkimediske faste størrelser i det 4. århundrede.
Spørgsmål: Hvorfor genopdagede kunstnere og matematikere de arkimediske faste legemer i renæssancen?
Svar: I renæssancen satte kunstnere og matematikere pris på rene former, og de arkimediske faste legemer blev betragtet som rene former.
Sp: Hvornår afsluttede Johannes Kepler sin søgen efter alle de arkimediske faste legemer?
Svar: Johannes Kepler afsluttede sandsynligvis søgningen efter alle de arkimediske faste størrelser omkring 1620.
Spørgsmål: Hvad skal der til for at konstruere et arkiimedisk fast stof?
Svar: For at konstruere et arkimedisk rum kræver det mindst to forskellige polygoner.
Søge