Conways Livsspil: Celleautomat, regler og historie
Opdag Conways Livsspil: forstå celleautomaten, reglerne, historien og eksempler på mønstre. Lær hvordan simple regler skaber kompleksitet — begynd her.
Conways Livsspil (ofte kaldet Game of Life) er en robotspil (cellular automaton), som blev skabt af den britiske matematiker John Horton Conway i 1970.
Navnet "spil" kommer af, at man kan opstille forskellige startkonfigurationer (mønstre) og se, hvordan de udvikler sig over tid efter faste regler. Det er dog et nulspiller-spil: når startkonfigurationen er givet, udvikler systemet sig automatisk uden yderligere indblanding. Mange studerer netop, hvordan små ændringer i startopsætningen kan give meget forskellige langtidsadfærd.
Regler
Livets spil foregår på et todimensionelt gitter af kvadrater (celler). Hver celle kan være enten levende eller død. Opdateringen sker i diskrete tidssteg, og alle celler opdateres samtidig efter disse simple regler, som anvender Moores nabolag (de otte omkringliggende celler):
- En levende celle med færre end to levende naboer dør (underbefolkning).
- En levende celle med to eller tre levende naboer fortsætter med at være levende (overlevelse).
- En levende celle med mere end tre levende naboer dør (overbefolkning).
- En død celle med præcis tre levende naboer bliver levende (fødsel).
På grund af disse simple, deterministiske regler kan komplekse og ofte uventede mønstre opstå over mange generationer.
Typiske mønstre og fænomener
- Still lifes (stabile mønstre): mønstre, der ikke ændrer sig fra generation til generation (fx "block" og "beehive").
- Oscillatorer: mønstre, der gentager sig selv efter et antal generationer (fx "blinker" med periode 2).
- Spaceships: mønstre, der bevæger sig hen over gitteret (fx "glider").
- Guns: mønstre, der konstant udsender andre mønstre, fx den berømte Gosper glider gun, som udsender glidere og dermed skaber uendelig vækst i et ubegrænset gitter.
Historie og betydning
Conway konstruerede Livets spil i 1970 som et simpelt eksperiment i cellulære automater. Spillet blev hurtigt populært efter omtale i tidsskriftet Scientific American af Martin Gardner. Et vigtigt resultat var opdagelsen af mønstre som glider gun og senere beviser for, at spillet er Turing-komplet—dvs. at det, med de rette konstruktioner, kan udføre enhver beregning, som en almindelig computer kan.
Livets spil har haft stor indflydelse på studiet af emergens, komplekse systemer og algoritmisk kunst, og det bruges både i undervisning og i matematisk forskning som et enkelt eksempel på, hvordan komplekst adfærd kan opstå fra enkle regler.
Praktisk: hvordan man spiller og implementerer
For at "spille" Livets spil vælger man en startkonfiguration af levende celler på et gitter og lader reglerne køre generation for generation. I praksis benyttes ofte computere eller browser-baserede simulatorer, der tillader:
- At tegne startmønstre manuelt eller indlæse færdige mønstre.
- At køre simulationen trinvis eller med konstant hastighed.
- At ændre gitterets størrelse og kantadfærd (fx faste kanter, wrap-around/torus eller et stort/ubegrænset gitter).
Ved implementering i kode er opmærksomhed på ydeevne vigtig for store gitterstørrelser; typiske optimeringer omfatter at holde styr på kun de celler, der kan ændre sig, eller at bruge effektive datastrukturer som hash-sæt til sparse gitterrepræsentationer.
Varianter
Der findes mange varianter af Livets spil med andre fødsels- og overlevelsesregler (fx "HighLife"), andre gittertyper eller flere tilstande end blot levende/død. Disse varianter undersøges for at forstå, hvordan regelændringer påvirker kompleksitet og adfærd.
Selvom reglerne er meget enkle, viser Conways Livsspil på overbevisende vis, hvordan rige og uforudsigelige mønstre kan opstå fra deterministic, lokale regler — et centralt tema i studiet af komplekse systemer.
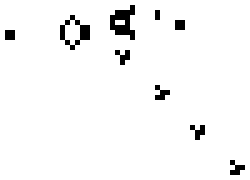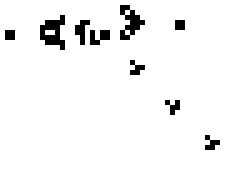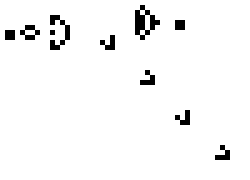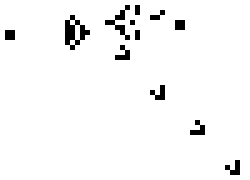
Gosper's Glider Gun, der skaber "svævefly".
Regler
Spillet spilles på et gitter af firkanter, der kaldes celler, og hver celle er sort (levende) eller hvid (død). Når folk spiller spillet, starter de med at gøre nogle døde celler levende. Derefter kan de levende celler gøre andre celler levende eller døde på grund af spillets regler. Reglerne er følgende:
- Enhver levende celle, der berører mindre end to levende naboer, dør.
- Enhver levende celle, der berører fire eller flere levende naboer, dør.
- En levende celle, der berører to eller tre levende naboceller, gør intet.
- Enhver død celle, der berører præcis tre levende naboceller, bliver levende.
Den måde, som en spiller placerer de første levende celler på, starter spillet. Det første niveau (generation) laves ved hjælp af de 4 regler. Når spilleren er færdig med at ændre cellerne, gør han det samme igen for at lave det næste niveau. Spillet er slut, når alle cellerne er døde eller alle cellerne er levende, eller når spillet gør det samme igen og igen. Livets spil er Turing-komplet.
Historie
John Horton Conway lavede Game of Life, fordi han ville vide, om han kunne lave en imaginær robot af celler, der kunne blive større. Han kombinerede en masse idéer inden for matematik for at lave reglerne for spillet. Det er et af de første "simulationsspil" nogensinde, som repræsenterer ting, der sker i det virkelige liv. Det er vigtigt, fordi det, når det bruges i kompliceret matematik, kan se på mange ting som fysik, biologi, økonomi og filosofi.
Mønstre
Mønstre er særlige ting, der sker i spillet. Der findes mange forskellige typer af mønstre, herunder statiske mønstre, hvor intet ændrer sig mellem banerne, gentagende mønstre, hvor de levende og døde celler gentages, og mønstre, der bevæger sig selv hen over brættet ("rumskibe"). Almindelige eksempler på disse tre klasser er vist nedenfor, med levende celler vist med sort og døde celler vist med hvidt.
| | | | | | | |
| Blok | Båd | Blinker | Tudse | Svævefly | LWSS | Pulsar |
"Blokken" og "båden" ændrer sig ikke, "blinkeren" og "tudsen" har to udseende, der gentager sig, og "svæveflyet" og "letvægtsrumskibet" ("LWSS") er rumskibe, der bliver ved med at bevæge sig hen over cellerne i hvert niveau. "Pulsar" er den mest almindelige gentagelse, der har 3 dele. De fleste gentagelsesmønstre har 2 dele, som f.eks. blinklyset og tudsen. [1].
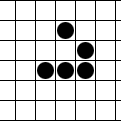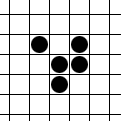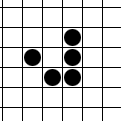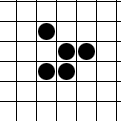
Udviklingen og bevægelsen af en "glider".
Variationer over livet
Siden Livets spil blev skabt, har nogle mennesker spillet med nye regler. Disse regler er som regel flere måder at gøre celler levende eller døde på, eller de er flere regler, der gør det sværere for cellerne at skifte.
Nogle variationer ændrer cellernes udseende eller placeringen af dem.
To spillere
Når to personer spiller Livets spil, har de levende celler to farver, og en spiller vinder, når alle cellerne er dækket af hans farver. Når en død celle bliver levende, får den samme farve som de levende celler, der rører ved den. Hvis begge farver rører ved den nye levende celle, vinder den farve, der rører den mest.
Spørgsmål og svar
Q: Hvem skabte Game of Life?
A: The Game of Life blev skabt af den britiske matematiker John Horton Conway.
Q: Hvornår blev Game of Life skabt?
A: Game of Life blev skabt i 1970.
Q: Er Game of Life et robotspil?
A: Ja, Game of Life er et imaginært robotspil, også kendt som en cellulær automat.
Q: Hvorfor kaldes Game of Life for et spil?
A: Game of Life kaldes et spil, fordi folk, der spiller det, kan sætte det op på forskellige måder for at få det til at gøre forskellige ting, og nogle gange ændrer de den oprindelige opsætning for at se, hvad der sker.
Q: Hvad betyder det, når Game of Life omtales som et zero-player-spil?
A: Game of Life er et zero-player-spil, fordi det ændrer sig, uden at nogen spiller, efter at startpositionen er valgt.
Q: Kan to spillere spille Game of Life sammen?
A: Nej, Game of Life er ikke designet til, at to spillere kan spille sammen. En anden type spil giver to spillere mulighed for at opstille imaginære robotter for at se, hvilken der er bedst.
Q: Er Game of Life et populært spil?
A: Ja, Game of Life er blevet ret populært og er blevet brugt som en model inden for forskellige områder som videnskab, kunst og filosofi.
Søge

