Kurvetilpasning: Definition, metoder (interpolation, udjævning, regression)
Kurvetilpasning: Lær definition, metoder (interpolation, udjævning, regression) og anvendelser — visualisering, ekstrapolering og håndtering af usikkerhed.
Kurvetilpasning er at konstruere en matematisk funktion, der passer bedst til et sæt datapunkter. Målet kan være at beskrive mønstre i data, at forudsige værdier mellem eller uden for observerede punkter, eller at kvantificere sammenhænge mellem variable.
Kurvetilpasning omfatter to overordnede tilgange: interpolation og udjævning. Interpolation kræver, at den tilpassede funktion går gennem (eller nøjagtigt gennem) de observerede datapunkter. Udjævning søger derimod en glat funktion, som beskriver den overordnede tendens i dataene uden at følge hvert enkelt støjpræget punkt. Et beslægtet felt er regressionsanalyse, som i højere grad inddrager statistisk inferens, herunder beregning af usikkerhed, konfidensintervaller og hypotesetests for parametre i modellen.
Hvorfor bruge kurvetilpasning?
- Visualisering: En tilpasset kurve gør det lettere at se tendenser og strukturer i støjfyldte data.
- Interpolation og imputation: Estimere værdier i mellemliggende punkter, hvor der ikke er målinger.
- Ekstrapolation: Forudsige værdier uden for det observerede område (dog med øget usikkerhed).
- Modellering: Kvantificere forhold mellem variable og teste hypoteser.
Almindelige metoder til interpolation
- Lineær interpolation: Simpelt og robust; forbinder punkter med rette linjer.
- Polynomiel interpolation: En enkelt polynomium bestående gennem alle punkter (f.eks. Lagrange). Kan give stor svingning (Runge-fænomen) for høje ordener.
- Stykvis polynomiel interpolation / splines: F.eks. kubiske splines, som passer glat gennem punkter og undgår store oscillationer ved at kombinere lokale polynomier.
- Rationelle funktioner og andre basisfunktioner: Bruges når modeller med polynomier passer dårligt.
Metoder til udjævning (smoothing)
- Gennemsnitsfiltre og bevægende gennemsnit: Simpelt og hurtigt, egnet til signalbehandling.
- Kernel-smoothing: Vægter nærliggende punkter med en kernelfunktion (f.eks. Gaussisk); breddeparameter styrer glatheden.
- LOESS / LOWESS: Lokalt vægtet regressionsfit — fleksibelt, ikke-parametrisk, god til at fange lokale variationer.
- Udjævningssplines og smoothing splines: Minimerer en kombination af residualfejl og funktionens ruhed (styrkes af en glathedsparameter).
- Regularisering: Tilføjer straf for store parametre (fx ridge, lasso) for at undgå overfitting og gøre modellen glattere.
Regressionsanalyse
Regressionsmetoder er ofte parametiske modeller, hvor man estimerer et sæt parametre, der bedst forklarer en afhængig variabel ud fra én eller flere uafhængige variable.
- Lineær regression (mindste kvadraters metode): Mest almindelige metode; estimerer koefficienter ved at minimere summen af kvadrerede residualer.
- Vægtet regression: Hver observation vægtes efter sin usikkerhed; nyttigt ved heteroskedasticitet.
- Generaliserede lineære modeller (GLM): Udvider lineær regression til ikke-normal respons (f.eks. logistisk regression).
- Robust regression: Mindsker indflydelsen fra outliers (f.eks. M-estimatorer).
- Regulariserede metoder (ridge, lasso, elastic net): Kontrollerer kompleksitet når der er mange forklarende variable og risiko for overfitting.
- Ikke-parametriske / semiparametriske metoder: Indbefatter GAMs (generalized additive models) og kernel-baserede regressorer, som tillader større fleksibilitet i formen af sammenhængene.
Modelvalg og vurdering af tilpasning
Vigtige principper og værktøjer til at vælge og vurdere en kurvetilpasning:
- Residualanalyse: Undersøg residualernes mønster for at afsløre systematiske fejl (ikke-tilfælde støj, heteroskedasticitet, autokorrelation).
- Goodness-of-fit: Mål som R², justeret R², RMSE (root mean squared error) giver kvantitativ vurdering af fit.
- Informationskriterier: AIC og BIC hjælper med at afveje modelkompleksitet mod passevne.
- Cross-validation: K-fold eller leave-one-out CV bruges til at estimere generaliseringsfejl og vælge modeller/smoothingsparametre.
- Konfidens- og predictionsintervaller: Angiv usikkerheden i parameterestimater og i fremtidige forudsigelser.
Numeriske og praktiske overvejelser
- Skalering af data: Standardisering kan forbedre numerisk stabilitet ved polynomier og regularisering.
- Overfitting vs. underfitting: For kompleks model fanger støj (overfitting); for simpel model fanger den ikke signalet (underfitting). Brug krydsvalidering til at finde balance.
- Runge-fænomen: Høje ordens globale polynomier kan give store oscillationer mellem punkter; foretræk lokale metoder (splines) i sådanne tilfælde.
- Valg af glathed/smoothingsparameter: Normalt bestemt ved krydsvalidering eller informationskriterier; har stor effekt på resultatet.
- Håndtering af uregelmæssigt fordelte datapunkter: Lokale metoder og vægtning kan være nødvendig, når datapunkter er tætte i nogle områder og sparsomme i andre.
Pitfalls og advarsler
- Ekstrapolation: Prognoser uden for det observerede område er usikre og afhængige af modelantagelser; vis forsigtighed.
- Tolkning: En god numerisk tilpasning betyder ikke nødvendigvis årsagssammenhæng — det kan være en empirisk beskrivelse uden underliggende mekanisme.
- Datafejl og outliers: Kan skævvride en tilpasning; overvej robust metoder eller rense/påvirk vægte.
- Modelkompleksitet: Flere frihedsgrader giver mere fleksibilitet, men også større risiko for at modellere tilfældig støj.
Kort praktisk vejledning
- Start med simpel model (fx lineær eller lav-orden spline) og inspektér residualer.
- Brug visualisering — plot data og den tilpassede kurve med konfidens- eller predictionsintervaller.
- Benyt krydsvalidering til valg af kompleksitet eller smoothing-parameter.
- Vær eksplicit omkring antagelser (lineæritet, uafhængighed, ens varians) og kontroller dem.
Tilsammen dækker kurvetilpasning både rene matematiske teknikker og statistiske metoder, fra eksakt interpolation til probabilistisk regressionsanalyse. Valget af metode afhænger af målet (præcis interpolation, støjreduktion, forudsigelse eller fortolkning), datakvalitet og krav til usikkerhedsvurdering.
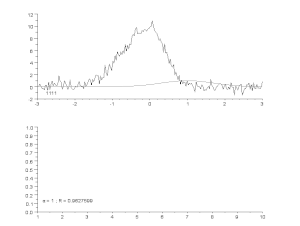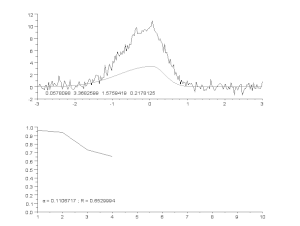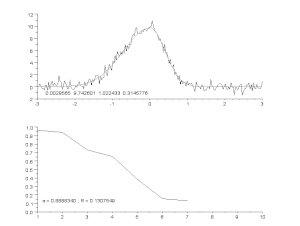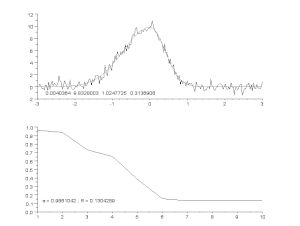
Tilpasning af en støjende kurve ved hjælp af en asymmetrisk topmodel med en iterativ proces (Gauss-Newton-algoritme med variabel dæmpningsfaktor α). Øverst: rådata og model. Nederst: udvikling af den normaliserede sum af fejlenes kvadrater.
Spørgsmål og svar
Q: Hvad er kurvepasning?
A: Kurvepasning er processen med at skabe en matematisk funktion, der passer bedst til et sæt datapunkter.
Q: Hvad er de to typer af kurvetilpasning?
A: De to typer af kurvepasning er interpolation og udjævning.
Spørgsmål: Hvad er interpolation?
Svar: Interpolation er en type kurvepasning, der kræver en nøjagtig tilpasning til dataene.
Spørgsmål: Hvad er udjævning?
Svar: Udglatning er en type kurvepasning, hvor der konstrueres en "glat" funktion, som passer til dataene tilnærmelsesvis.
Spørgsmål: Hvad er regressionsanalyse?
Svar: Regressionsanalyse er et beslægtet emne, der fokuserer på spørgsmål om statistisk inferens, f.eks. hvor stor usikkerhed der er i en kurve, som er tilpasset data, der er observeret med tilfældige fejl.
Spørgsmål: Hvad er nogle anvendelser af tilpassede kurver?
Svar: Tilpassede kurver kan bruges til at visualisere data, gætte værdier for en funktion, hvor der ikke er data til rådighed, og opsummere sammenhænge mellem to eller flere variabler.
Spørgsmål: Hvad er ekstrapolation?
Svar: Ekstrapolering er brugen af en tilpasset kurve uden for de observerede datas område. Dette er imidlertid behæftet med en vis usikkerhed, da det kan afspejle den metode, der er anvendt til at konstruere kurven, lige så meget som det afspejler de observerede data.
Søge