AlegsaOnline.com

Heaviside-funktion (enhedstrin): definition, egenskaber og anvendelser

Heaviside-funktion: klar definition, vigtige egenskaber og praktiske anvendelser i styringsteori, signalbehandling og matematik – inkl. Hʼ=δ og illustrative eksempler.

Forfatter: Leandro Alegsa

15-02-2026

Heaviside-funktionen H er en ikke-kontinuerlig funktion, hvis værdi er nul for et negativt input og én for et positivt input.

Funktionen bruges i styringsteoriens matematik til at repræsentere et signal, der tændes på et bestemt tidspunkt og forbliver tændt på ubestemt tid. Den er opkaldt efter englænderen Oliver Heaviside.

Heaviside-funktionen er integralet af Dirac-deltafunktionen: H′ = δ. Dette skrives undertiden som H′(t) = δ(t), hvor denne lighed forstås i distributions- (generaliserede funktioner) forstand.

Formel og konvention ved t = 0

En almindelig piecewise-definition er

H(t) =

0, for t < 0
1, for t > 0

Værdien i t = 0 er ikke entydigt bestemt af definitionen ovenfor, og der anvendes forskellige konventioner i praksis:

H(0) = 0 eller H(0) = 1 — ofte benyttet i ingeniørpraksis afhængigt af konteksten.
H(0) = 1/2 — en matematisk symmetrisk konvention, som er nyttig ved Fourier- og Laplace-transformer og når man ønsker at gøre sammenhængen H′ = δ konsekvent i distributionsforstand.

Egenskaber

Shifts: H(t - a) er en step der tænder ved t = a. Dens distributionelle afledte er d/dt H(t - a) = δ(t - a).
Skalering: H(a t) er en skaleret step; for a > 0 bevarer den kausalitetens struktur, for a < 0 ændres orienteringen.
Komplement: For t ≠ 0 gælder H(-t) = 1 − H(t). Ved t = 0 afhænger identiteten af den valgte værdi H(0).
Relation til fortegnsfunktionen: For t ≠ 0 gælder sgn(t) = 2H(t) − 1.
Konvolution: Konvolution med et signal f giver en akkumuleret (causal) integral: (H * f)(t) = ∫_−∞^t f(τ) dτ.
Transforms:
- Laplace-transform: L{H(t)} = 1/s for Re(s) > 0 (med passende fortolkning ved s = 0 afhængigt af H(0)).
- Fourier-transform: F{H(t)} kan skrives som PV(1 / (jω)) + π δ(ω) (PV = principal value), når H(0) tages som 1/2 i distributions-forstand.

Relation til Dirac-delta og distributioner

Heaviside-funktionen og Dirac-deltaen er relaterede gennem differentiation i distributionsforstand: den distributionelle afledte af H er δ. Dette betyder, at for enhver testfunktion φ(t) gælder

∫ H(t) φ′(t) dt = −φ(0), hvilket svarer til ⟨H′, φ⟩ = ⟨δ, φ⟩.

Fra en fysisk synsvinkel kan δ(t) ses som et uendeligt kort, men med endeligt areal, "spring" i H(t).

Anvendelser

Signalbehandling: Modellering af tænd/sluk-signaler, pulsformning og systemers step-respons.
Kontrolteori og systemanalyse: Bruges til at beskrive inputter, som skifter værdi pludseligt; step-responsen giver information om stabilitet og transientadfærd.
Elekronik og kredsløb: Anvendt til at beskrive påsætning af en spænding eller strøm ved t = 0, og til at finde impuls- og step-responser i lineære kredsløb.
Differentialligninger: Ved tvungen eksitation med et step kan man løse ODE'er stykkevist (før og efter step) og bruge kontinuitetsbetingelser ved t = step.
Matematik og teori om distributioner: Heaviside er et grundlæggende eksempel på en distribution, der er ikke-differentiabel i klassisk forstand, men har en veldefineret distributionsafledte.

Tilnærmelser og glatning

I numeriske beregninger og simuleringer glattes Heaviside ofte ved at bruge kontinuerte approximationer, f.eks. logistiske eller arctan-baserede funktioner:

Logistisk approximation: H(t) ≈ 1 / (1 + e^{−k t}) med k → ∞ giver et skarpt step.
Arctan-tilnærmelse: H(t) ≈ 1/2 + (1/π) arctan(k t).

Glatning gør det muligt at anvende standardnumerik (f.eks. differentiering) uden ustabiliteter forårsaget af diskontinuiteten.

Eksempel

Et simpelt eksempel i kredsløb: En spænding kildes som V(t) = V₀ H(t) repræsenterer en konstant spænding V₀, der tilsluttes ved t = 0. Reaktionen i et RC-kredsløb på en sådan step giver den velkendte step-respons, som kan udledes ved løsning af differentialligningen med input V₀ H(t).

Heaviside-funktionen er således et enkelt men kraftfuldt værktøj i anvendt matematik, fysik og ingeniørvidenskab til at beskrive pludselige ændringer og kausale systemer.

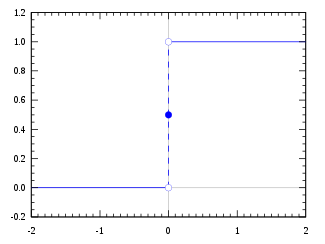
Heaviside-trinsfunktionen ved anvendelse af halvmaksimum-konventionen

Diskret form

Vi kan også definere en alternativ form af Heaviside-trinsfunktionen som en funktion af en diskret variabel n:

H [ n ] = { 0 , n < 0 1 , n ≥ 0 {\displaystyle H[n]={\begin{cases}0,&n<0\\\\1,&n\geq 0\end{cases}}} $H[n]={\begin{cases}0,&n<0\\1,&n\geq 0\end{cases}}$

hvor n er et heltal.

Eller

H ( x ) = lim z → x - ( ( ( | z | / z + 1 ) / 2 ) {\displaystyle H(x)=\lim _{z\rightarrow x^{-}}}((|z|/z+1)/2)} $H(x)=\lim _{z\rightarrow x^{-}}((|z|/z+1)/2)$

Den diskrete tidsenhedsimpuls er den første forskel af det diskrete tidstrin

δ [ n ] = H [ n ] - H [ n - 1 ] . {\displaystyle \delta \left[n\right]=H[n]-H[n-1]. } $\delta \left[n\right]=H[n]-H[n-1].$

Denne funktion er den kumulative summering af Kronecker-deltaet:

H [ n ] = ∑ k = - ∞ n δ [ k ] {\displaystyle H[n]=\sum _{k=-\infty }^{n}\delta [k]\,} $H[n]=\sum _{k=-\infty }^{n}\delta [k]\,$

hvor

δ [ k ] = δ k , 0 {\displaystyle \delta [k]=\delta _{k,0}\,} $\delta [k]=\delta _{k,0}\,$

er den diskrete enhedsimpulsfunktion.

Repræsentationer

Ofte er det nyttigt at anvende en integral repræsentation af Heaviside-trinsfunktionen:

H ( x ) = lim ϵ → 0 + - 1 2 π i ∫ - ∞ ∞ ∞ 1 τ + i ϵ e - i x τ d τ = lim ϵ → 0 + 1 2 π i ∫ - ∞ ∞ ∞ 1 τ - i ϵ e i x τ d τ . {\displaystyle H(x)=\lim _{\epsilon \til 0^{+}}-{1 \over 2\pi \mathrm {i} }\int _{-\infty }^{\infty }{1 \over \tau +\mathrm {i} \epsilon }\mathrm {e} ^{-\mathrm {i} x\tau }\mathrm {d} \tau =\lim _{\epsilon \to 0^{+}}}{1 \over 2\pi \mathrm {i} }\int _{-\infty }^{\infty }{1 \over \tau -\mathrm {i} \epsilon }\mathrm {e} ^{\mathrm {i} x\tau }\mathrm {d} \tau . } $H(x)=\lim _{\epsilon \to 0^{+}}-{1 \over 2\pi \mathrm {i} }\int _{-\infty }^{\infty }{1 \over \tau +\mathrm {i} \epsilon }\mathrm {e} ^{-\mathrm {i} x\tau }\mathrm {d} \tau =\lim _{\epsilon \to 0^{+}}{1 \over 2\pi \mathrm {i} }\int _{-\infty }^{\infty }{1 \over \tau -\mathrm {i} \epsilon }\mathrm {e} ^{\mathrm {i} x\tau }\mathrm {d} \tau .$

H(0)

Funktionens værdi ved 0 kan defineres som H(0) = 0, H(0) = ½ eller H(0) = 1.

H ( x ) = 1 + sgn ( x ) 2 = { 0 , x < 0 1 1 2 , x = 0 1 , x > 0. {\displaystyle H(x)={\frac {1+\operatorname {sgn}(x)}{2}}={\begin{cases}0,&x<0\\{\frac {1}{2}},&x=0\\1,&x>0.\end{cases}}} $H(x)={\frac {1+\operatorname {sgn}(x)}{2}}={\begin{cases}0,&x<0\\{\frac {1}{2}},&x=0\\1,&x>0.\end{cases}}$

Relaterede sider

Laplace-transformation

Spørgsmål og svar

Q: Hvad er Heaviside-funktionen?

A: Heaviside-funktionen er en ikke-kontinuerlig funktion, hvis værdi er nul for et negativt input og én for et positivt input.

Q: Hvorfor bruges Heaviside-funktionen i kontrolteori?

A: Heaviside-funktionen bruges i kontrolteori til at repræsentere et signal, der tændes på et bestemt tidspunkt og forbliver tændt på ubestemt tid.

Q: Hvem er den person, som Heaviside-funktionen blev opkaldt efter?

A: Heaviside-funktionen er opkaldt efter englænderen Oliver Heaviside.

Q: Hvad er forholdet mellem Heaviside-funktionen og Dirac-delta-funktionen?

A: Heaviside-funktionen er integralet af Dirac-deltafunktionen: H′(x)= δ(x).

Q: Hvad giver Heaviside-funktionen som output for positive input?

A: Heaviside-funktionen udsender én for positive input.

Q: Hvad udsender Heaviside-funktionen for negative input?

A: Heaviside-funktionen udsender nul for negative input.

Spørgsmål: Hvilken type funktion er Heaviside-funktionen?

A: Heaviside-funktionen er en ikke-kontinuerlig funktion.