Lavineeffekten (avalanche-effekten) i kryptografi — definition og betydning
Lavineeffekten i kryptografi: hvordan små inputændringer skaber store outputændringer — afgørende for sikre blokchifre og hashfunktioners robusthed og modstandsdygtighed.
Lavineeffekten ("jordskredseffekten") er en egenskab ved algoritmer til blokchifre og kryptografiske hashfunktioner. Den er ofte ønsket i kryptografi. Effekten betyder kort sagt, at en lille ændring i input fører til en stor og tilsyneladende tilfældig ændring i output. I gode blokchiffrer vil en enkelt bitændring i enten nøglen eller i klarteksten medføre, at en betydelig del af cifferteksten ændrer sig — typisk omkring halvdelen af bitsene.
Lavineeffekten opnås typisk ved at kombinere ikke-lineære komponenter (fx S‑bokse) med permutationer og gentagne iterationer (runder). Når en algoritme har tilstrækkelige runder, kan en lille ændring "spredes" hurtigt: hver bit i output får afhængighed af mange eller alle input-bits. Denne udbredelse af inputpåvirkninger er tæt forbundet med Shannons principper om forvirring og diffusion.
Historie og formelle kriterier
Udtrykket lavineeffekt blev først brugt af Horst Feistel (Feistel 1973). For at måle og formulere ønskede egenskaber har kryptografer udviklet mere præcise kriterier:
- Avalanche-kriteriet: En enkelt-bit ændring i input bør ændre omtrent halvdelen af output-bits.
- Strict Avalanche Criterion (SAC): Hver output-bit bør ændre sig med sandsynlighed 1/2, når én input-bit inverteres.
- Bit Independence Criterion (BIC): Ændringer i to forskellige output-bits skal være uafhængige, når man ændrer en enkelt input-bit.
Hvorfor det er vigtigt
Hvis en block cipher eller en kryptografisk hash-funktion ikke udviser en stærk lavineeffekt, giver det dårlig randomisering. En kryptoanalytiker kan i så fald udnytte mønstre i output til at lave forudsigelser om input eller nøglemateriale. Manglende lavineeffekt kan gøre algoritmen sårbar over for angrebstyper som differential- og lineær kryptoanalyse, og det kan i ekstreme tilfælde være tilstrækkeligt til helt eller delvist at bryde (knække) algoritmen.
Implementering og designvalg
Lavineeffekten er en af de primære designmålsætninger, når man skaber en stærk kryptering eller en kryptografisk hashfunktion. Designere bruger flere teknikker for at opnå den:
- Flere runder (iterationer), så små ændringer får tid til at sprede sig.
- Ikke-lineære komponenter (fx S‑bokse) for at skabe kompleksitet.
- Permanente permutationer og bitmixere for at sikre diffusion.
- Komplekse nøgleplaner, så en lille ændring i nøglen gavner lavineeffekten.
Matematisk set anvender man idéer fra kaosteori (sammenlignet med sommerfugleeffekten) som en metafor for, hvordan små inputændringer kan få stor og uforudsigelig effekt i output. Derfor er mange moderne blokchiffrer designet som produktchiffrer, der kombinerer flere simple transformationer til en kompleks helhed. Tilsvarende har mange hash-funktioner store datablokke og flere runder i deres kompressionsfunktioner for at opnå god lavineeffekt.
Test og måling
Lavineeffekten testes empirisk med bl.a.:
- Hamming-distance tests: måling af hvor mange bits, der ændrer sig i gennemsnit ved enkelt-bit-flip i input.
- Statistiske tests (fx chi‑kvadrat, tilfældighedstest) for at vurdere fordelingen af ændringer.
- SAC- og BIC-tests for at kontrollere sandsynligheder og uafhængighedsegenskaber.
Et godt design viser cirka 50 % ændrede output-bits ved en enkelt-bit ændring i input over et repræsentativt sæt af prøver.
Begrænsninger og praktiske overvejelser
Selvom en stærk lavineeffekt er nødvendig for sikkerhed, er den ikke alene tilstrækkelig. Andre egenskaber som høj ikke-linearitet, modstandskraft mod specielle angreb (fx svage nøgler, sidekanalangreb) og korrekt protokolbrug (fx sikre initialiseringsvektorer og modes i blokchifre) er også afgørende. I nogle anvendelser (fx visse driftstilstande for blokchifre) vil en enkelt-bit ændring i plaintext ikke sprede sig samme måde — her spiller modes of operation en rolle for, hvordan ændringer påvirker efterfølgende blokke.
Konsekvenser for hashfunktioner
For kryptografiske hashfunktioner sikrer lavineeffekten, at en lille ændring i meddelelsen giver et helt anderledes digest. Det gør det vanskeligere at finde to forskellige input, der giver samme output (kollision) eller at forudsige input ud fra digestet (preimage). Manglende lavineeffekt i en hash kan resultere i lettere collision-angreb eller andre svagheder i sikkerhedsprotokoller, der bygger på den.
Samlet set er lavineeffekten et centralt designmål i moderne kryptografi: den sikrer, at små inputændringer fører til store, uforudsigelige outputændringer, hvilket er essentielt for både konfidensialitet og integritet i sikre systemer.
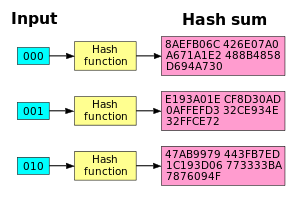
SHA1-hashfunktionen har en god lavineeffekt. Når en enkelt bit ændres, bliver hashsummen helt anderledes.
Navn
Navnet har sin oprindelse i jordskred. En lille sten kan falde ned, gå sammen med noget sne og skabe et ødelæggende jordskred. Stenen var lille, men kunne forårsage mange ødelæggelser. Det er det samme som det, denne virkning gør. En lille ændring i input (stenen) skal ændre output (landskabet).
Strengt lavinekriterium
Det strenge lavinekriterium (SAC; et "stærkt jordskredskriterium") er en egenskab ved boolske funktioner. Det er af betydning for kryptografi. Det er opfyldt, hvis alle outputbits ændres med en sandsynlighed på 50 %, hvis en enkelt inputbit ændres.
SAC blev bygget på begreberne evolutionskomplethed og lavine. Det blev introduceret af Webster og Tavares i 1985. I dag er det et krav til ethvert moderne kryptografisk system. Det blev f.eks. opfyldt af alle finalisterne i AES-konkurrencen.
Kriterium for bituafhængighed
Bit-uafhængighedskriteriet (BIC; et kriterium, der er uafhængigt af bit) er et kriterium. Det lyder således: Når en enkelt indgangsbit ændres (inverteres), skal to udgangsbits ændres uafhængigt af hinanden. Dette gælder for alle bits.
Det ville f.eks. ikke være tilfredsstillende, hvis den ene udgangsbit kun ændres, når den anden udgangsbit også ændres. De ændrer sig måske kun, fordi input-bitten ændres. I modsat fald ville outputbitsne afhænge af hinanden.
Relaterede sider
- Forvirring og spredning
Spørgsmål og svar
Spørgsmål: Hvad er lavinteffekten?
A: Lavineeffekten (også kendt som "jordskredseffekten") er en egenskab ved blokchifre og algoritmer med kryptografiske hashfunktioner, som siger, at en lille ændring i nøglen eller klarteksten bør medføre en kraftig ændring i cifferteksten.
Spørgsmål: Hvem brugte først udtrykket "lavineeffekt"?
A: Udtrykket lavineeffekt blev første gang brugt af Horst Feistel i 1973.
Spørgsmål: Hvordan hænger det sammen med Shannons egenskab om forvirring?
A: Begrebet lavineeffekt blev identificeret ved Shannons egenskab af forvirring, som fastslår, at hvis en blokchiffer eller kryptografisk hashfunktion ikke opfylder denne grad i væsentlig grad, så har den dårlig randomisering og kan delvist eller helt brydes (knækkes).
Spørgsmål: Hvad er nogle af designmålene, når man skaber stærke krypteringssystemer?
A: Når folk skaber stærke krypteringskoder, forsøger de at bygge en god lavineeffekt ind i dem ved hjælp af matematiske principper som f.eks. sommerfugleeffekten. Dette er grunden til, at de fleste blokchiffrer er produktchiffrer, og at hash-funktioner har store datablokke.
Spørgsmål: Hvad sker der, hvis en algoritme ikke opfylder lavinteffekten?
Svar: Hvis en algoritme ikke opfylder lavineeffekten i væsentlig grad, er den dårligt randomiseret og kan helt eller delvist knækkes (crackes) af kryptoanalytikere, der kan forudsige input på grundlag af et givet output.
Spørgsmål: Hvorfor bruger de fleste blokchifre produktchifre?
Svar: De fleste blokchifre anvender produktchifre, fordi de hjælper med at bygge gode avalanceeffekter ind i dem ved hjælp af matematiske principper som f.eks. sommerfugleeffekten.
Spørgsmål: Hvorfor har hash-funktioner store datablokke?
Svar: Hash-funktioner har store datablokke, fordi det hjælper med at opbygge gode avalanceeffekter ved hjælp af matematiske principper som f.eks. sommerfugleeffekten.
Søge