Parallakse: definition og astronomisk afstandsmåling
Forstå parallakse og astronomisk afstandsmåling: hvordan jordens bane, vinkler, parsecs og missioner som Hipparcos/Gaia bruges til præcise afstande til stjerner.
Parallakse er den opfattede ændring i positionen af et objekt, når det betragtes fra to forskellige observationspunkter. I sin enkleste form er parallakse et geometrisk forskydningsfænomen: et nærliggende objekt skifter mere i forhold til en fjern baggrund end et fjernt objekt, når observationspunktet flyttes.
Parallakse i astronomien
Inden for astronomi er den årlige parallakse den eneste direkte metode til at bestemme afstanden til stjerner uden for solsystemet. Når man observerer en stjerne fra Jorden på forskellige tidspunkter af året, fx seks måneder fra hinanden, ses en lille tilsyneladende forskydning i stjernens position på himlen som følge af Jordens bevægelse omkring Solen. Denne vinkel måles og bruges i et trigonometri-stykke til at finde stjernens afstand.
Hvordan målingen udføres
Parallaksen måles som vinklen mellem to observationslinjer til stjernen. For den årlige stjerneparallakse betragtes typisk vinklen p, defineret som halvdelen af den samlede årsbetingede forskydning; basen i trekanten er så 1 astronomisk enhed (1 AU, afstanden fra Jorden til Solen). Da Jordens bane er kendt præcist, kan længden af grundlinjen og de målte vinkler indgå i et trekantsberegningsproblem, og afstanden udledes ved hjælp af trigonometri.
Enheder og formel
Den almindelige enhed for stjerneparallakse er buesekunder (arcseconds). Én buesekund er 1/3600 af en grad. Den astronomiske afstandsenhed parsec er netop defineret ud fra parallakse: 1 parsec (pc) er den afstand, hvor 1 AU ser ud til at give en parallakse på 1 buesekund. Det betyder, at sammenhængen simple kan skrives som:
- d (i parsec) = 1 / p (i buesekunder)
- eller omvendt: p (i\") = 1 / d (i pc)
Hvor p er den årlige parallakse. For meget små vinkler anvendes ofte millibuesekund (mas, 1 mas = 0,001\") og for de mest præcise moderne målinger mikro-buesekunder (µas).
Eksempel
Et konkret eksempel: en stjerne med parallakse p ≈ 0,77\" ligger i størrelsesordenen 1 / 0,77 ≈ 1,3 parsec, hvilket svarer til omkring 4,24 lysår. Dette illustrerer, hvordan selv små vinkler svarer til relativt korte astronomiske afstande.
Begrænsninger og fejlkilder
Metoden har naturlige begrænsninger: hvis et objekt er så fjernt, at Jordens bane kun giver en ubetydelig parallakservinkel, bliver målingen upræcis eller umulig. For stjerner yderst langt borte bliver parallaksen mindre end de målbare grænser. Traditionelt blev denne grænse ofte sat til nogle få hundrede lysår med jordbaserede instrumenter, men moderne rumteleskoper har rykket grænsen betydeligt.
Andre fejlkilder er atmosfærisk turbulens (for jordbaserede observationer), instrumentstøj, fejl i kalibrering, stjernens egen bane (f.eks. i binære systemer), og fejl ved bestemmelsen af referencestjernernes afstande. Der skelnes desuden mellem relativ parallakse (målt i forhold til baggrundsstjerner) og absolut parallakse, hvor der korrigeres for referencestjernernes egne bevægelser eller afstande.
Historie og moderne rummissioner
Parallaksemetoden har været grundlæggende i opbygningen af den kosmiske afstandsstige — den rækkefølge af metoder, astronomer bruger til at bestemme større og større afstande i universet. Fra 1989 til 1993 foretog Hipparcos-satellitten målinger af over 100.000 nærliggende stjerner med en typisk nøjagtighed på størrelsesordenen millibuesekunder. Gaia (rumfartøj) har som mål at måle positioner og parallakser for omkring en milliard stjerner med langt højere præcision (for de lyseste stjerner ned til mikro-buesekund-niveau), hvilket kraftigt udvider den direkte rækkevidde af parallaksebaserede afstande.
Anvendelser ud over stjerner
Astronomer bruger princippet om parallakse til at måle afstande til mange himmellegemer: til Månen og Solen (diurnal og solparallakse), til nærliggende planeter og til stjerner uden for solsystemet. For objekter i vores eget solsystem eller månen kan parallakse også måles fra forskellige punkter på Jorden (diurnal parallakse), hvor baseline er Jordens diameter i stedet for 1 AU.
Parallakse i biologisk syn
Mange dyr, inklusive mennesker, har to øjne, hvilket giver dybdeopfattelse gennem binokulær parallakse; dette kaldes stereopsis. Fordi de to øjne sidder forskudt på hovedet, ser hvert øje motivet fra en let forskellig vinkel, og hjernen bruger denne forskel til at vurdere afstand. En beslægtet mekanisme er bevægelsesparallakse (motion parallax), hvor afstand opfattes ved at observere relativ bevægelse af objekter, når betrageren selv bevæger sig. Begge mekanismer er grundlaget for vores normale 3D-opfattelse af en scene.
Samlet set er parallakse et simpelt og meget fundamentalt geometrisk værktøj i astronomien: hvor det kan anvendes, giver det de mest direkte og pålidelige afstandsmål — og danner dermed fundamentet for alle efterfølgende afstandsmetoder i kosmologi og astrofysik.
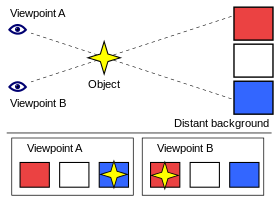
Et eksempel på et objekts parallakse i forhold til en fjern baggrund som følge af en ændring i placering. Set fra "Standpunkt A" ser objektet ud til at være foran den blå firkant. Når synspunktet ændres til "synspunkt B", synes objektet at være flyttet foran den røde firkant.
Spørgsmål og svar
Q: Hvad er parallakse?
A: Parallakse er den opfattede ændring i positionen af et objekt set fra to forskellige steder. Den måles ved vinklen mellem to observationslinjer og kan bruges til at bestemme afstande.
Sp: Hvordan bruges parallakse i astronomi?
A: I astronomien er den årlige parallakse den eneste direkte måde at måle afstanden til stjerner uden for solsystemet på. Astronomer bruger princippet om parallakse til at måle afstanden til himmellegemer, herunder til Månen, Solen og stjerner uden for solsystemet.
Spørgsmål: Hvordan beregner man afstand ved hjælp af parallakse?
Svar: Astronomiske positionsmålinger foretages på forskellige tidspunkter af året. Da man kender Jordens bane nøjagtigt, kan man beregne afstanden fra position 1 til position 2. Vinklen fra horisonten til objektet kan måles præcist, hvilket giver en trekant, hvis grundlinje og vinkler er kendt nøjagtigt. Ud fra denne trekant kan trigonometri anvendes til at beregne afstande udtrykt i parsecs.
Spørgsmål: Er der nogen begrænsninger ved at bruge parallakse til at måle fjerne objekter?
A: Ja, det slår fejl med objekter, der er så langt væk, at Jordens bane er for lille til at give en tilstrækkelig stor parallaxvinkel til nøjagtige målinger - ca. 100 lysår væk eller mere. Der er opfundet andre metoder, men ingen af dem er lige så nøjagtige som parallaksen for relativt nærliggende objekter.
Spørgsmål: Hvilken satellit blev brugt i 1989-1993 til at måle nærliggende stjerner?
Svar: Hipparcos-satellitten blev brugt i denne periode til at foretage målinger af over 100.000 nærliggende stjerner.
Spørgsmål: Hvilken rumsonde vil foretage lignende målinger som Hipparcos gjorde? Svar: Gaia (rumfartøj) vil foretage lignende målinger af omkring en milliard stjerner.
Søge